The proof of the Goldbach's Conjecture is one of the biggest still unsolved problems regarding prime numbers. Originally expressed in 1742 by the mathematician Christian Goldbach, from whom the conjecture takes its name, it was rephrased by Euler in the form in which we know it today:
Every even number greater than 2 can be expressed as a sum of two prime numbers.
In spite of the empirical evidence and the simplicity of its statement, the conjecture is resisting to every attempts of proof since almost three centuries. Several mathematicians have proved some weaker versions of the conjecture.
The statement phrased by Christian Goldbach is a "conjecture", so, as a matter of principle, it is a hypothesis. This means that it can be:
- True, that is all even numbers greater than 2 can be expressed as a sum of two prime numbers;
- False, that is at least one even number greater than two exists, which cannot be written as a sum of two prime numbers.
Currently, there are several attempts to prove the Goldbach's conjecture, which are complete, in the sense that they come to the conclusion, but contain a series of problems, so they have not been considered valid by the international community. We instead propose some proof strategies, which are still far from being complete, but already contain interesting and unrefuted (so far) intermediate results. We hope this material will be a useful starting point for who, like us, has started looking for a proof...
The statement phrased by Christian Goldbach is a "conjecture", so, as a matter of principle, it is a hypothesis. This means that it can be:
- True, that is all even numbers greater than 2 can be expressed as a sum of two prime numbers;
- False, that is at least one even number greater than two exists, which cannot be written as a sum of two prime numbers.
Goldbach's conjecture is put into the field of Number theory, the branch of Mathematics which studies the properties of integer numbers. In order to understand the proofs of the results similar to the conjecture, and very likely also to prove the conjecture itself, a sound knowledge of number theory is required. But this kind of knowledge rarely is part of a mathematician's curriculum...
Dashed line theory is a new mathematical theory which studies the connection between the sequence of natural numbers and their divisibility relationship. Typical problems are the computation of the n-th natural number divisible by at least one of k fixed numbers, or not divisible by any of them. Due to this nature, the theory is suited for studying prime numbers with a constructive approach, inspired to the sieve of Eratosthenes...
Goldbach's conjecture is put into the field of Number theory, the branch of Mathematics which studies the properties of integer numbers. In order to understand the proofs of the results similar to the conjecture, and very likely also to prove the conjecture itself, a sound knowledge of number theory is required. But this kind of knowledge rarely is part of a mathematician's curriculum...
Dashed line theory is a new mathematical theory which studies the connection between the sequence of natural numbers and their divisibility relationship. Typical problems are the computation of the n-th natural number divisible by at least one of k fixed numbers, or not divisible by any of them. Due to this nature, the theory is suited for studying prime numbers with a constructive approach, inspired to the sieve of Eratosthenes...
Latest posts
As we have seen, some parameters λd appear in the Selberg's sieve formula, which are used both in the estimation of the sieve function and in the related error term. In this article we'll calculate these parameters in order to obtain the lowest possible estimate.
In this article we'll begin to get to the heart of sieve theory, analyzing in detail the so-called "Selberg's sieve". It is not, in reality, a new sieve (comparable for example to that of Eratosthenes); the sieve (understood as a function) is always the general one, Selberg obtained an overestimation of it. In summary, we can say that what is called "Selberg sieve" is actually a way of overestimate a sieve function with a function simple to calculate, composed of two terms: an estimate and an error term.
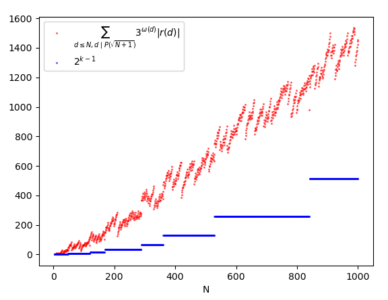
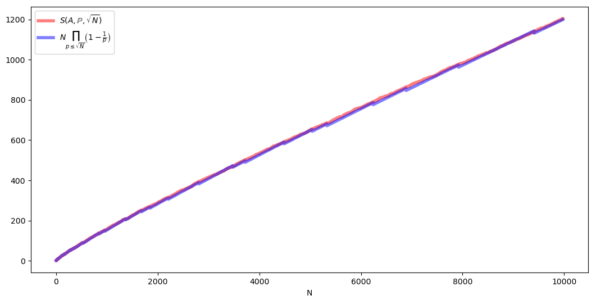
In the previous article we calculated the sieve function of Erathostenes' sieve starting from the algorithm, obtaining a formula with a number of terms that grows exponentially with respect to the number of primes used, therefore too complex to be used in practice. But ultimately it is not necessary to calculate a sieve function exactly: to be able to study it (for example to understand its asymptotic behavior) it would be sufficient to find a good approximation. Therefore, if we were content to approximate the sieve function, in the case of Eratosthenes' sieve, would we obtain a less complicated formula?…
In the previous article we examined in detail the sieve of Eratosthenes, both at an algorithmic level and as a sieve function. We have seen that there is a strong connection between the two formulations, as the sieve function calculates how many elements remain in the set {2, 3, 4, ..., N} after having applied the algorithm. But so, to calculate the sieve function, why not start from the study of the algorithm from which it originates? In this article and the next one we'll see that this idea does not work in practice, and we'll understand why.
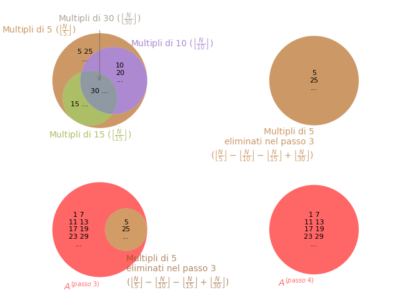
In the previous article we saw that the proof of Chen's Theorem is based on sieve theory. But what is a sieve? In this article we'll explain it based on the most famous example of a sieve, that of Eratosthenes. It allows you to answer a simple question: given an integer N ≥ 2, what are the prime numbers less than or equal to N?