Prerequisites:
- Computation of spaces in second order linear dashed lines
- Inclusion-exclusion principle (preferential)
By now, the formula for calculation of \mathrm{t\_space} for a linear dashed line of any order is not yet known, but, how we have seen in the section about dashed line theory, some partial results exist, which could bring, once extended, to a general formula. The only already known formulas are the one for first order dashed lines of type (n_1):
and the one for second order dashed lines of type (n_1, n_2):
where S(T) is the number of spaces within a period of the dashed line.
Continuing in the article, we will see how it is possible to reason to obtain a formula for orders greater than two, and what are the difficulties encountered. Precisely because of these difficulties, it also makes sense to look for a formula that can approximate \mathrm{t\_space}, keeping a good compromise between the goodness of approximation and the complexity of the formula. We will mention this possibility in the last part of the article.
Before going on, it is worth noting that another possible way to look for a valid formula regardless of the order is to proceed indirectly. As the formulas for calculating \mathrm{t\_space} become more and more complex as the order increases, a different approach could be adopted: that is, rather than looking for a formula, determining a characterization, that is, a criterion which tells us which columns are spaces. After having found it, the criterion obtained could be used as a basis for obtaining an actual formula.
The search for a characterization of the spaces that is valid for all dashed lines, regardless of their order, is still an open question, and it is dealt with in a dedicated page , in which the progress of our investigation in this direction can be found.
How can we reason to get a formula for \mathrm{t\_space} for any order
Even if we still don’t have a formula that calculates the function \mathrm{t\_space} for linear dashed lines of higher order than the second one, we can characterize it as the solution of an equation, as we did for the second order. To derive this equation, however, it is necessary to change the approach: it is not enough, as we did for second order dashed lines, to count the dashes by columns and by rows, but we must resort to a general mathematical principle, known as inclusion-exclusion principle. Let’s see how to apply it in our case.
Let T = (n_1, ..., n_k) be a linear dashed line of order k > 1, x a fixed positive integer, and s := \mathrm{t\_space}_T(x). Since s is the x-th space of T, the first s columns of T can be divided into x spaces and s - x columns containing at least one dash. The problem is now to count these columns with a different formula, so that, as we did for second order dashed lines, by equating this formula with s - x we can obtain an equation from which to derive s as a function of x.
First, let’s introduce a notation that can be useful: we’ll indicate with C(i) the set of columns less than or equal to s which are divisible by n_i, for i = 1, \ldots, k. We are interested in knowing how many columns less than or equal to s are divisible by at least a component, that is, those belonging to at least one of these k sets. But saying that a column belongs to at least one of the sets C(1), \ldots, C (k) is equivalent to saying that it belongs to their union, C(1) \cup \ldots \cup C(k): this is the set of columns less than or equal to s divisible by at least one component. As we said, it has s - x elements, so the equation we were looking for is:
Let’s consider the dashed line T = (2, 3, 5), and let is x = 10. How it’s possible to see, for example, with the dashed line viewer, we have \mathrm{t\_space}_T(10) = 37: this is our s. The sets C(1), C(2), C(3) of the columns divisible respectively by 2, 3 and 5, less than or equal to 37 are:
Their union, viewed in Figure 1, is
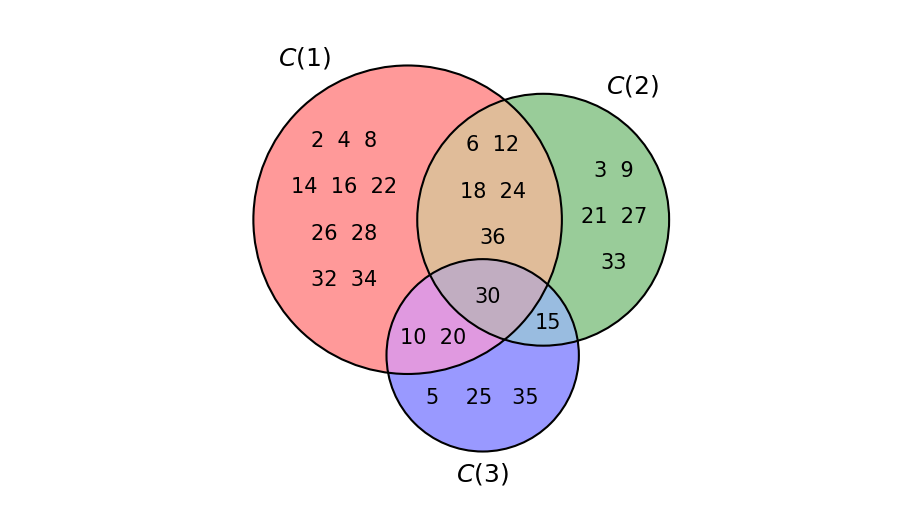
So, we have s - x = 37 - 10 = 27 = |C(1) \cup C(2) \cup C(3)|: then, equation (1), in our case, is verified.
At this point the inclusion-exclusion principle comes into play, which allows to calculate, in general, the number of elements of the union of several sets.
The inclusion-exclusion principle
We can imagine the inclusion-exclusion principle, applied to the sets C(1), \ldots, C(k), as a calculation algorithm which proceeds this way:
- Let’s initialize a counter m := 1. We will increase this counter by one unit at a time, up to the number of components k.
- Let’s list all possible combinations, without repetition, of m indices chosen among 1, \ldots, k:
- If m = 1, the possible combinations without repetition of 1 index are the indices themselves: 1, \ldots, k
- If m = 2, the possible combinations without repetition of 2 indices are (1, 2), (1, 3), (1, 4), \ldots, (1, k), (2, 3), (2, 4), \ldots, (2, k), (3, 4), \ldots, (3, k), \ldots, (k - 1, k)
- If m = 3, the possible combinations without repetition of 3 indices are (1, 2, 3), (1, 2, 4), \ldots, (1, 2, k), (1, 3, 4), (1, 3, 5), \ldots, (1, 3, k), \ldots, (1, k-1, k), (2, 3, 4), (2, 3, 5), \ldots, (k - 2, k - 1, k)
- …
- For each combination of indices j_1, \ldots, j_m found in the previous step, let’s count the number of elements of the intersection of the sets C(j_1), \ldots, C(j_m):
- If m = 1, we are considering only one set at a time and therefore there is no intersection to perform; the elements of each set are simply counted, |C(1)|, \ldots, |C(k)|
- If m = 2, we must calculate |C(1) \cap C(2)|, |C(1) \cap C(3)|, |C(1) \cap C(4)|, \ldots, |C(1) \cap C(k)|, |C(2) \cap C(3)|, |C(2) \cap C(4)|, \ldots, |C(2) \cap C(k)|, |C(3) \cap C(4)|, \ldots, |C(3) \cap C(k)|, \ldots, |C(k-1) \cap C(k)|
- If m = 3, we must calculate |C(1) \cap C(2) \cap C(3)|, |C(1) \cap C(2) \cap C(4)|, \ldots, |C(1) \cap C(2) \cap C(k)|, |C(1) \cap C(3) \cap C(4)|, |C(1) \cap C(3) \cap C(5)|, \ldots, |C(1) \cap C(3) \cap C(k)|, \ldots, |C(1) \cap C(k - 1) \cap C(k)|, |C(2) \cap C(3) \cap C(4)|, |C(2) \cap C(3) \cap C(5)|, \ldots, |C(k - 2) \cap C(k - 1) \cap C(k)|
- …
- All the counts obtained in the previous step are added, taking them with the sign + if m is odd, with the sign – if m is even:
- If m = 1, the sum (with the sign +) is |C(1)| + \ldots + |C(k)|
- If m = 2, the sum is -(|C(1) \cap C(2)| + |C(1) \cap C(3)| + \ldots + |C(k-1) \cap C(k)|)
- If m = 3, the sum is |C(1) \cap C(2) \cap C(3)| + |C(1) \cap C(2) \cap C(4)| + \ldots + |C(k - 2) \cap C(k - 1) \cap C(k)|
- …
- If m \lt k, we’ll increment m and go back to step 2. If m = k, we’ll proceed to next step.
- In the end, all the partial results obtained in step 4 are added together, and the result is the number of elements of C(1) \cup \ldots \cup C(k).
All that we have presented in an algorithmic form can be expressed in a compact way with the following formula, which constitutes the statement of the inclusion-exclusion principle applied to sets C(1), \ldots, C(k):
The classic proof of the inclusion-exclusion principle is purely technical, based on the induction principle. However, we are not so interested in reporting this proof, which is easy to find, as in illustrating the idea behind it.
Let’s start from the initial goal, which was to count the columns containing at least one dash, i.e. divisible by at least one of the components of the dashed line. We can first count the divisible ones for each component of the dashed line. By counting them separately and adding it all together, in the end we’ll have a total of:
Thus we have obtained the first term of the formula of the inclusion-exclusion principle. The problem is that, if we stopped here, we would count twice the columns which are divisible by two components. For example, if a column is divisible by both n_1 and n_2, in formula (3) we count it for the first time among those divisible by n_1 and a second time between those divisible by n_2, and the same thing applies to the columns divisible by any pair of components n_i and n_j ( where 1 \leq i \lt j \leq k). Since all these columns have been counted twice in (3), we can try to correct our counting by subtracting them from the previous formula:
But even so the count is still not correct. In fact, if a column is divisible by three components of the dashed line (if it has at least three components), in the formula (4) it is counted:
- Three times in the first summation, once for each component for which it is divisible
- Less three times in the second summation, one for each pair of components for which it is divisible. In fact, if a column is divisible by three components n_a, n_b and n_c, it is obviously divisible by the same components taken in pairs, i.e. n_a and n_b, for n_a and n_c, and for n_b and n_c, then it falls three times in the second summation of (4), with (i, j) = (a, b), (i, j) = (a, c) and (i, j) = (b, c).
So in fact the columns divisible by three components are not counted at all in (4), because they give the total count equal contributions in absolute value, but of opposite sign. Then we can think of extending the formula (4) by adding just the number of these columns:
However, neither this formula can work in general, because at this point, as you can imagine, the columns divisible by four components (if there are some) would not be counted correctly. We could go on, including a further summation the purpose of which is correcting the count of these columns, and so on. Certainly, however, this procedure cannot go on indefinitely, because the components of the dashed line are k, which is a finite number, and it makes no sense to ask if there are columns divisible by a number of components greater than k. This is the intuitive reason why the formula with k summations is the correct one when the number of starting sets is k, exactly as asserted by the inclusion-exclusion principle.
For k = 3, then considering three sets C(1), C(2) and C(3), we’ll have:
- For m = 1, we must count, with a positive sign, the number of elements of each set taken individually
- For m = 2, we must count, with a negative sign, the number of elements of C(1) \cap C(2), C(1) \cap C(3) e C(2) \cap C(3)
- For m = 3 = k, last value of m to be considered, we must count, with positive sign, the number of elements of teh only intersection possible of three sets, i.e. C(1) \cap C(2) \cap C(3)
Then, formula (2) will become:
Returning to the previous example, we have that (see Figure 1):
Then:
which is precisely the number of elements of the union C(1) \cup C(2) \cup C(3), as we have verified in the previous example.
Characteristic equation of linear \mathrm{t\_space} of generic order
Returning to the dashed lines, we can combine the formulas (1) and (2), obtaining:
We can calculate |C(i)|, |C(i) \cap C(j)|, |C(i) \cap C(j) \cap C(l)|, \ldots, |C(1) \cap \ldots \cap C(k)| applying the Proposition T.2 (Count of dashes up to a certain value in a first order linear dashed line), in a fully similar way as we did in order to obtain the Proposition T.7 (Characteristic equation of second order linear \mathrm{t\_space}). So, we have
Replacing in (6), we have:
Thus we have obtained an equation in which in principle we could derive s, starting from the x that we had fixed a priori. Reasoning as for the Proposition T.7, we can obtain that this equation, together with the constraint that its solutions are spaces, characterizes the spaces of the dashed line, in the sense of the following Proposition:
General characteristic equation of linear \mathrm{t\_space}
Let T be a linear dashed line of order k. Then
The formula at the right of the equivalence symbol in (9) is named general characteristic equation of linear \mathrm{t\_space}.
For k = 3, starting from (9), we’ll obtain the following characteristic equation of linear third order \mathrm{t\_space}:
For example, for the dashed line T = (2, 3, 5) the equation will become:
For x = 10, and by consequence s = 37, we’ll find ourselves with the calculations of the previous example, as:
If k = 2 were set in (9), we would obtain again the characteristic equation of the second order, the one that appears in the Proposition T.7. If we want, we could also set k = 1, obtaining the characteristic equation of the first order, the one of the Proposition T.3. For this reason, in Proposition T.8, we did not make assumptions about the order, thus also including the case of first order dashed lines. However, this is a degenerate case that would not affect the functioning of the inclusion-exclusion principle: therefore, at the beginning, we assumed k \gt 1, although technically this constraint on k is not necessary.
Why solving the general characteristic equation is so difficult
In principle, by solving equation (9) in the unknown s, you could calculate \mathrm{t\_space} for linear dashed lines of any order. Let’s see why this is very difficult.
The difficulty in solving equation (9) lies in the number of integer parts it contains. In the article about \mathrm{t\_space} for second order, we have seen that it is already quite difficult to solve such equation with two integer parts (see formula (8′) of the Theorem T.12 (Solution of the modified characteristc equation of second order linear \mathrm{t\_space})), in fact we have not reported the proof because it consists of several pages full of calculations. We have also seen that solving an equation with three integer parts is possible thanks to a small technical artifice. But in general, what can we expect? If, as it seems, the difficulty of solving the equation increases with the number of integer parts, we would have to worry, because the number of integer parts of the equation (9), for the order k, is exactly 2^k - 1: the growth in the number of integer parts of the general characteristic equation is exponential.
The cause of this explosion in the number of integer parts is the inclusion-exclusion principle. Going back to the reasoning that led us to formula (9), we can observe that there is an integer part for every possible non-empty subset of the k indices 1, \ldots, k: from the subsets of a single element, which give rise to the integer parts \left \lfloor \frac{s}{n_1} \right \rfloor, \ldots, \left \lfloor \frac{s}{n_k} \right \rfloor, up to the only subset of k elements, i.e. the set of all indices, which gives rise to the integer part \left \lfloor \frac{s}{\mathrm{lcm}(n_1, \ldots, n_k)} \right \rfloor. But the number of possible subsets of a set of k elements is 2^k; excluding the empty set, we have the formula 2^k - 1, therefore this is also the number of integers in equation (9).
This exponential growth can already be observed for k = 1, 2, 3:
- For k = 1, 2^k - 1 = 2 - 1 = 1 integer part: it’s the one which appears in the formula (4) of the Proposition T.3 (Characteristic equation of first order linear \mathrm{t\_space})
- For k = 2, 2^k - 1 = 4 - 1 = 3 integer parts: they are the ones which appear in the formula (8) of theProposition T.7 (Characteristic equation of second order linear \mathrm{t\_space})
- For k = 3, 2^k - 1 = 8 - 1 = 7 integer parts: they are the ones which appear in the formula (9′) of this article
In short, if solving the second order equation is already complicated, which has only three integer parts, we can imagine how complicated is solving the third order equation, which has 7 ones, not to mention the subsequent orders, which have, in the order, 15, 31, 63, 127, etc..
Fortunately in mathematics there are often multiple ways to solve the same problem, and in this case we can hope that solving the general characteristic equation is not the only way to calculate \mathrm{t\_space}.
An important open point is to find other ways of obtaining a general formula for \mathrm{t\_space}, without explicitly solving the characteristic equation.
Approximation of \mathrm{t\_space}
One way of answering the previous open point, partially circumventing the problem, is not to try to calculate \mathrm{t\_space}, since it is so difficult, but to find an approximation. Ideally, it would be a good thing to establish a relationship that applies to any linear dashed line T, of type
where f and \delta are functions to be determined, and \delta is as small as possible. Of course, you could also choose different functions \delta(x) on the right and left, but this would not change the substance, so we prefer the above formulation, which, if desired, can be abbreviated as
Actually, we have already seen something like this. We mentioned it talking about first order dashed lines, when after the Theorem T.1 (Formula for computing the linear first order \mathrm{t\_space} function) we observed that if the integer part is removed from the characteristic equation (in the first order there is only one), we’ll get a much simpler equation to solve, the solution of which s \approx \frac{n_1 x}{n_1 - 1} is very similar to that of the characteristic equation, which is s = \left \lfloor \frac{n_1 x - 1}{n_1 - 1} \right \rfloor . So in this case our f is given by f(x) = \frac{n_1 x}{n_1 - 1}. As for \delta, a possible choice in this case is the constant function 1, since
This relationship can be easily proved; by the way, it could also be observed that instead of the 1 that appears on the right with the role of \delta(x), there could be a 0. Too bad it is a relationship of little use, because the first order function \mathrm{t\_space} is so simple that it doesn’t need to be approximated.
We can make a similar argument for the second order, assuming for simplicity that the two components are coprime, i.e. that \mathrm{lcm}(n_1,n_2) = n_1 n_2. With this assumption, if from formula (8) of the Proposition T.7 we remove the integer parts, and of consequently we replace the equality symbol with approximate equality (\approx), it will become:
This equation can be solved easily:
The fraction multiplying x is interesting:
- The numerator is the length of the dashed line period (remember that the components are coprime)
- The denominator is the number of spaces in a period (v. Property T.7 (Computation of the number of spaces in a second order linear dashed line) and the remark which follows it)
It can be proved that this holds in general: given any linear dashed line T, starting from the general characteristic equation and removing all the integer parts from it, we’ll obtain a very simple equation to solve, the solution of which is x that multiplies the fraction
which for second order dashed lines, as in (11), is
This fraction represents the constant distance that would occur between two consecutive spaces of a dashed line T, if they were uniformly distributed over the period (as it happens for example for dashes on a row). We are therefore saying that the function \mathrm{t\_space} for a linear dashed line T could be approximated as follows:
Hence, with reference to (10), the function x d_T would have the role of f, and \delta would be to be determined. The spaces of a period of T would therefore be roughly, in order, d_T, 2 d_T, 3 d_T, ..., \text{length of a period of } T (the last space is obtained by placing x = \text{number of spaces in a period of } T in the formula (12)). So d_T would not only be the constant distance between two consecutive spaces, but would also coincide with the first space.
Unfortunately such linear hatches do not exist. The only linear dashed line that has equidistant spaces between them is the dashed line (2), for which d_T = \frac{2}{1} = 2, but d_T does not coincide with the first space, which it is 1:

For all the other linear dashed lines, the spaces are not evenly distributed, as can be easily seen in all the other examples of linear dashed lines presented so far. Despite this, the dashed line model with evenly distributed spaces seems to describe linear dashed lines quite well, from a statistical point of view. We will deepen the details in a dedicated article, but certainly it is not enough to stop here: you have to look for an approximation of \mathrm{t\_space} which represents a good compromise between degree of approximation and simplicity of functions f[/latex and [latex]\delta involved. This remains an open point.
The field of investigation is therefore to find two functions f and \delta such that for each linear dashed line T we have:
The function \delta should be as small as possible, and, at the same time, the functions f e \delta should not be too complicated.