The goal
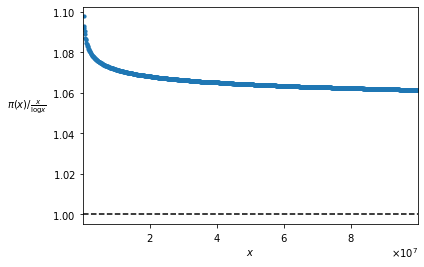
The “strong version” of Chebyshev’s Theorem (according to some authors, simply “Chebyshev’s Theorem”) constitutes, with respect to the weak one, a further step towards the Prime Number Theorem. In fact, the two Theorems are very similar, since they study the same functions, in the same way. In both cases, the functions which are studied are \pi(x), which returns the number of prime numbers less than or equal to x, and \frac{x}{\log x}; the way of studying them consists in calculating their ratio, and seeing how it behaves as x increases. The strong version of Chebyshev’s Theorem establishes that there are only two possibilities: either this ratio has no limit, i.e. it continues to oscillate to infinity, or, if it tends to a limit, that limit is 1. The Prime Number Theorem goes further, saying that the first possibility cannot happen: the ration between \pi(x) and \frac{x}{\log x} tends to 1.
So the strong version of Chebyshev’s Theorem can be regarded as an intermediate result between the weak version and the Prime Number Theorem: its statement is very similar to the one of the Prime Number Theorem, but it keeps some of the vagueness of the weak version, according to which the functions \pi(x) and \frac{x}{\log x} have generically “the same order of magnitude”.
The path
This path extends the one about the weak version of Chebyshev’s Theorem. In fact, we’ll see that it’s possible to pass from the weak version to the strong one by the application of some fundamental techniques, starting from a particular way for calculating areas, up to the study of the order of magnitude of the harmonic series and the factorial.
Map of paths for number theory
General introduction to paths