Prerequirements:
- Chebyshev’s Theorem (weak version)
- The lemma of bar chart area
- From real numbers to integer numbers
- The factorial function and the Lambda* function
- The limit inferior and the limit superior of a sequence
In this post we’ll revisit Chebyshev’s Theorem, according to which the function \pi(x), that counts the number of prime numbers less than or equal to a positive integer x, has the same order of magnitude as \frac{x}{\log x}. We’ll see that not only the two functions have the same order of magnitude, but also that, if a limit for their ratio exists, that limit must be 1; so, we’ll obtain a “stronger” version of the Theorem.
Recall that, in order to obtain Chebyshev’s Theorem, we first studied the functions \theta(x) and \psi(x), establishing that they are asymptotically equivalent and that they have order x (Theorem N.4). Similarly, for obtaining the stronger version of the Theorem, we’ll focus on one of these functions, \psi(x).
The proof is interesting from a technical point of view, because it puts several previous results altogether:
- The starting point is the connection between the functions \Lambda^{\star} and \psi^{\star} given by Property N.6;
- By expressing this connection in logarithmic form, we can apply to it the lemma of bar chart area;
- Theorem N.4 (Asymptotic equivalence and order of magnitude of \theta(x) and \psi(x)) and Proposition N.7 (Order of magnitude of the factorial-like function based on \Lambda^{\star}) let compute the order of magnitude of two out of the three terms appearing in the so obtained equality;
- Reasoning about the remaining term, we can obtain some information about the limit superior and the limit inferior of the function \frac{\overline{\psi}(t)}{t}, an extension of \frac{\psi(x)}{x};
- Finally, remembering the asymptotic equivalence between \pi(x) and \frac{\psi(x)}{\log x} (Corollary of Theorem N.5), we can obtain the strong version of Chebyshev’s Theorem.
Let’s see these passages in more details. Let’s start from Property N.6 (Connection between \Lambda^{\star} and \psi^{\star}):
Starting from this relationship, we can obtain a more useful one by applying logarithm to both members:
where the function \Lambda, according to our usual notations, is defined as the logarithm of \Lambda^{\star}:
Function \Lambda
We define the function \Lambda: \mathbb{N}^{\star} \rightarrow \mathbb{R} such that:
The \Lambda function is known as von Mangoldt’s function, in honour of the German mathematician Hans von Mangoldt, who first defined it. Its value can be computed by using the factorizer.
On careful reading, (2) greatly resembles the basic assumption of the lemma of bar chart area, where we have n rectangles having as base respectively c_1, \ldots, c_n, and we indicate by C_k the sum of the first k bases, i.e. C_k = \sum_{i = 1}^k c_i. Here we have different symbols: r instead of i, x instead of k, \Lambda(r) instead of c_i and \psi(x) instead of C_k, but, after these replacements, formula (2) matches perfectly with the formula C_k = \sum_{i = 1}^k c_i that appears in the statement of the lemma. So we can imagine a bar chart made up of x rectangles, where the r-th rectangle, for r=1,\ldots,x, has for base \Lambda(r), and the sum of all the bases is \psi(x). Concerning the function that in the lemma is indicated by f, that is the function representing the heights, we can choose the most convenient one; in this case, for some reasons that will be clear in a while, we’ll let the height of the r-th rectangle to be \frac{1}{r} (see Figure 1):
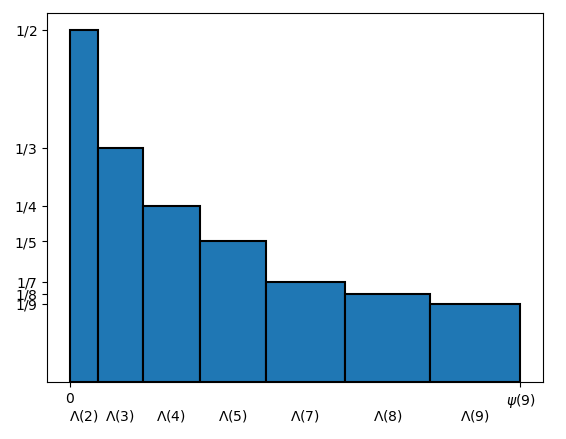
Now, thanks to the second form of the lemma of bar chart area, we can express the area of the bar chart in two different ways, obtaining the following equality:
In our case, in order to apply Lemma N.5 (Lemma of bar chart area, second form), we have to set:
- n := x
- c_i := \Lambda(i)
- C(k) := \sum_{i = 1}^k \Lambda(i) = \psi(k)
- f(i) := \frac{1}{i}
- \widetilde{f}(t): [1, n + 1) \rightarrow \mathbb{R} \text{ such that } \widetilde{f}(t) := \frac{1}{t} (an extension of f)
With these choices, we’ll obtain:
That is identical to (3), except the name of the variable in the summation.
The integral that appears in formula (3) may start from 2 instead of 1. In fact \psi(1) = \Lambda(1) = 0, so the simple extension \overline{\psi} is always zero in the interval [1, 2), thus zeroing the integral in this interval.
About the term \frac{\psi(x)}{x}, we already know its asymptotic order. In fact, by Theorem N.4 (Asymptotic equivalence and order of magnitude of \theta(x) and \psi(x)), the function \psi(x) has order x and so \frac{\psi(x)}{x} has order 1, i.e., by Property A.7, it’s a definitively bounded function. So we can rewrite (3) as follows:
The reason why we chose \frac{1}{r} for the height of the rectangles is indeed for generating the term \frac{\psi(x)}{x}, that we easily simplified using Theorem N.4.
Concerning the first term, we can compute its order of magnitude by the properties of the function \Lambda^{\star} and its relationship with the factorial function, as we saw in the post 13. The factorial function and the Lambda* function. In particular, this term can be obtained by the following corollary of Proposition N.7 (Order of magnitude of the factorial-like function based on \Lambda^{\star}):
Order of magnitude of the factorial-like function based on \Lambda^{\star}, logarithmic version
By applying the logarithm to both members of Proposition N.7, we’ll obtain:
From which, dividing all by a factor x, we’ll obtain the statement of the Corollary. When dividing by x, we used Property A.8A, by which \frac{O(x)}{x} = \frac{x \cdot O(1)}{x} = O(1).
Substituting into (4), we’ll have:
hence, by applying the properties of asymptotic orders Corollary 3 of Property A.8 and Corollary of Property A.9, we’ll obtain:
This equation can give us some information about the function \frac{\overline{\psi}(t)}{t}, that we may highlight inside the integral:
The question can be expressed in a more general way by the following question: if a function f: [1, +\infty) \rightarrow \mathbb{R} satisfies the equation
what can we say about f?
First of all, if in (5) we substitute f = 1 (the constant function with value 1) we’ll have that:
So choosing f = 1 the numbers check out. But not necessarily f has to be always constant with value 1. Intuitively, since the integral operation computes the area between the graph of f and the horizontal axis, f may oscillate above and below the value 1, but in such a way that the area of the parts where it’s above 1 compensate the ones where it’s below, and the total area is still \log x plus a definitively bounded amount. The important thing is that the area parts where the function is greater than 1 are “not too big” with respect to those ones where the function is less than one: there must be some balance.
In order to translate this intuition into more formal terms, we can use the concepts of limit superior and limit inferior, that we saw in the last post. In fact it can be proved that, if f satisfies (5), the following couple of inequalities must be true:
Here the limit superior and the limit inferior are applied to a function, whereas in the last post we always applied them to sequences; however their definitions are similar in the two cases. For example Definition A.7, according to which any interval greater than [\lim \inf f_n, \lim \sup\ f_n] contains almost all the terms of a sequence (f_n), remains the same if, instead of the sequence (f_n), a function f(t) is considered. The only thing that changes is the definition of “almost all the terms”, that in the case of sequences means all except a finite number; in the case of functions the concept is slightly more complex, but very similar, and for the sake of brevity we’ll not cover it for the moment.
In our case f(t) = \frac{\overline{\psi}(t)}{t}, so we may rewrite (6) as:
Indeed, getting back to integer numbers, it can be proved that the same relationships are still true if the function \psi: \mathbb{N}^{\star} \rightarrow \mathbb{N} is considered instead of its simple extension \overline{\psi}: \mathbb{R}^{\star} \rightarrow \mathbb{N}:
But this is a delicate passage on which we’ll return in the next posts. For now we’ll settle for the partial result given by (6′):
Limit inferior and limit superior of the function \frac{\overline{\psi}(t)}{t}
Let’s consider equation (5) and suppose that \lim \inf f \gt 1. If instead of f we had a sequence f_n, by Definition A.7 we could conclude that any interval greater than [\lim \inf f_n, \lim \sup f_n] contains almost all the terms of the sequence. But if \lim \inf f_n \gt 1, it means that almost all the sequence terms are greater than 1. In fact, if we set \delta := \lim \inf f_n - 1, so that \lim \inf f_n = 1 + \delta, then the interval [1 + \frac{\delta}{2}, \lim \sup f_n] is greater than [\lim \inf f_n, \lim \sup f_n], so it contains almost all the sequence terms. So almost all the sequence terms are greater or equal to 1 + \frac{\delta}{2}, and so they are greater than 1. But this means that the number of sequence terms less than or equal to 1 is finite (this terminology was introduced in the last post). Then certainly there exists an index N such that f_N is the last sequence term less than or equal to 1; equivalently, we can say that for all n \gt N, all the terms of the sequence are greater than 1.
Coming back to the function f, even if we did not see the definition of limit superior and limit inferior for functions, we can imagine that, by a similar argument, the conclusion would be the same: if \lim \inf f \gt 1, there would be a real number T such that, for all t \gt T, f(t) \gt 1.
Now let’s come back to equation (5). It’s a functional equation: it says that the integral \int_1^x f(t) \frac{1}{t} dt, seen as a function of x, is equal to the function \log x plus a definitively bounded function. The question is: does this equation remain true if we suppose the existence of this T?
Since it’s an asymptotic equation, we have to see what happens when x tends to infinity. So let’s imagine to compute the integral \int_1^x f(t) \frac{1}{t} dt, starting from x = 1, for increasing values of x. Initially x will always be less than or equal to T: the first value greater than T will be x = \left \lfloor T \right \rfloor + 1. Up to that value we’ll have obtained a certain value for the integral:
but this value doesn’t matter: we’ll indicate it with a constant A. Instead it’s more interesting to see what happens when continuing to increase x. In this case we may break the integral into two parts, as follows:
In this new integral, the function f is always greater than 1, because t \geq \left \lfloor T \right \rfloor + 1 \gt T. Since f is greater than 1, we can equivalently say that f \geq 1 + \epsilon for some constant \epsilon \gt 0. So we can continue the previous equalities as follows:
Hence, grouping all the constants into a single constant B, we’ll obtain:
If (5) was true, it should be B + \epsilon x = O(1), i.e. the function B + \epsilon x should be definitively bounded. But this is not true, because as x increases we would obtain greater and greater values of this function, since \epsilon \gt 0. Having obtained this contradiction, it means that our starting assumption, \lim \inf f \gt 1, is false: so, if (5) is true, it must be \lim \inf f \leq 1.
Concerning the limit superior, we can reason similarly starting from the assumption that \lim \sup f \lt 1. We would conclude that, if (5) is true, that assumption must be false, so it must be \lim \sup f \geq 1.
Finally, substituting f(t) = \frac{\overline{\psi}(t)}{t}, as we said before, we can obtain formula (6′).
We can rewrite the statement of Theorem N.7 as follows:
Now we can use the asymptotic equivalence between \pi(x) and \frac{\psi(x)}{\log x} (Theorem N.5). By appropriately modifying the proof of this theorem (but for the sake of brevity we’ll not do it), it can be proved that not only the two functions are asymptotically, equivalent, but that also their extensions \overline{\pi}(t) and \frac{\overline{\psi}(t)}{\log t} are. So, in the calculation of both the limit inferior and the limit superior, we can replace \frac{\overline{\psi}(t)}{\log t} by \overline{\pi}(t), obtaining:
Rewriting this equation in a slightly different form, the following Corollary arises:
Limit superior and limit inferior of the function \overline{\pi}(t) / \frac{t}{\log t}
The Corollary is depicted in Figure 2, where for the sake of simplicity only the values of the functions \overline{\pi}(t) / \frac{t}{\log t} for the integer variable x \in \mathbb{N}^{\star} are shown.
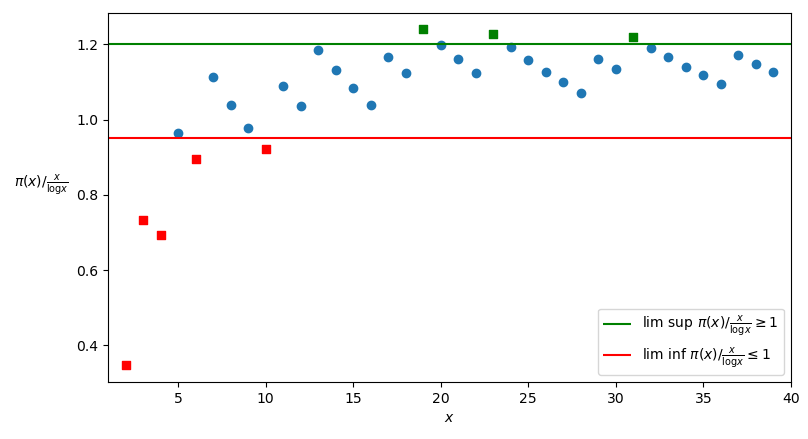
If we apply Property A.3 (A real sequence has a limit if and only if its \lim \inf and its \lim \sup are equal) to the statement of the Corollary, we’ll obtain in fact the following alternative version of it, that is the one we’ll call “string version” of Chebyshev’s Theorem (according to other authors, simply “Chebyshev’s Theorem”):
Chebyshev’s Theorem: strong version
If the function \pi(x) / \frac{x}{\log x} tends to a limit, that limit is 1.
Let’s suppose that the function \overline{\pi}(t) / \frac{t}{\log t} tends to a limit l. By Property A.3 (A real sequence has a limit if and only if its \lim \inf and its \lim \sup are equal), which can be proved for functions too, it must be:
But if \lim \inf \overline{\pi}(t) / \frac{t}{\log t} and \lim \sup \overline{\pi}(t) / \frac{t}{\log t} are equal, by the Corollary of Theorem N.7 they cannot be both 1, so, by (7), l = 1 and then \lim_{t \to +\infty} \overline{\pi}(t) / \frac{t}{\log t} = 1.
Finally, if \lim_{t \to +\infty} \overline{\pi}(t) / \frac{t}{\log t} = 1, also \lim_{x \to \infty} \pi(x) / \frac{x}{\log x} = 1, because the latter function (or, better, sequence) is a restriction on \mathbb{N}^{\star} of the former (generally, if \lim_{t \to +\infty} f(t) = l, also \lim_{n \to +\infty} f(a_n) = l, for any sequence a_n which tends to +\infty).
The strong version of Chebyshev’s Theorem seems to be denied by Figure 2, where it seems that the values of the function \pi(x) / \frac{x}{\log x} tend to be greater than 1. Indeed, if we extended the graph, we would see that the values of the function indeed tend to 1, but decreasing in an extremely slow fashion. In order to have an idea of how slow is this decrease, we can see the function graph for x \leq 100,000,000 (Figure 3):
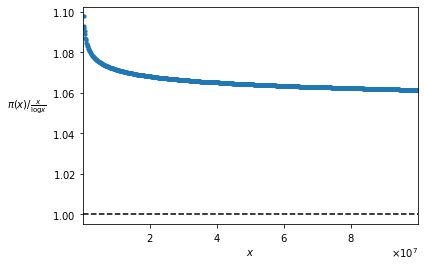
The function seems to never arrive to 1; but we just proved that, if a limit exists, that limit is 1. This is one of the cases when theory can show things that are difficult to see in practice, at least in the numerical orders which we are accustomed to.
For understanding why this Corollary is called “strong version” of Chebyshev’s Theorem, we have to remember the previous (“weak”) version of the Theorem (Corollary II of Theorem N.5):
According to this asymptotic relationship, by la Definition A.4 (Asymptotic relationships, alternative definitions using limits), if a limit for the ratio \pi(x) / \frac{x}{\log x} exists, it may be any non-zero real constant. In this sense, the “strong” version is so called because it limits this constants much more strongly, saying that it must be 1.
The strong version of Chebyshev’s Theorem is very similar to the prime number Theorem, which we stated in the introduction, according to which:
or equivalently, again by Definition A.4:
The only difference between the prime number Theorem and the strong version of Chebyshev’s Theorem is that the latter does not establish the existence of the limit, but it only says that if the limit exists, it’s equal to 1. So, in order to arrive to the prime number Theorem, it remains to be proved that the function \pi(x) / \frac{x}{\log x} tends to a limit. This is a very complex part of the proof of the prime number Theorem, which will be covered in the next posts.