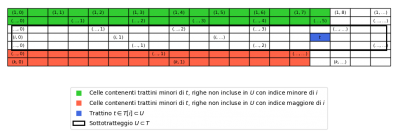
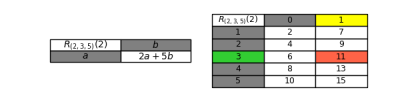
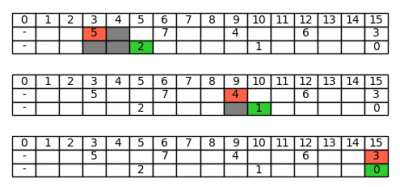
Dashed line theory is a new mathematical theory which studies the connection between the sequence of natural numbers and their divisibility relationship. Typical problems are the computation of the n-th natural number divisible by at least one of k fixed numbers, or not divisible by any of them. Due to this nature, the theory is suited for studying prime numbers with a constructive approach, inspired to the sieve of Eratosthenes...
The birth of the theory was among the school desks, with the aim of creating a useful tool for the proof of the Goldbach's conjecture.
When the maths teacher of Simone, during the third year of high school, told him about the Goldbach’s conjecture, he felt the irresistible desire for understanding it deeply, in order to try to prove it. Some classmates followed his first reasoning, but their interest didn’t come from the problem itself, but from the one million dollar prize which at that time would have been won by whoever was able to prove it. For Simone the prize was important too, but not as much as the desire for knowing the mechanisms that conceal themselves under the simple statement of the conjecture. So his classmates soon lost interest in that matter, while he was busy, in the next years, in developing a new mathematical theory that he believed a useful tool for the proof. He named it dashed line theory.
But why conceiving a new theory, just for solving a specific problem? He thought that, if nobody was able to prove the conjecture yet, a reason could be the lack of the right mathematical tools. So it was worth the effort to try with a new approach, based on a new theory.
In 2010 the theory was published for the first time in a complete form, in Italian, in the website http://teoriadeitratteggi.webnode.it, but with a very formal language, which leaves little space to intuition. This aspect has been improved since 2018, with the birth of the Let's prove Goldbach! project, thanks to which the topics of dashed line theory have been explained in a more instructive way, with the help of images and examples. The result are the posts listed below.
Still as a part of the Let's prove Goldbach! project, the theory was further developed, when looking for the proof of the Goldbach's conjecture. Soon we'll gather most of these developments into a new section of this site.
As an internal reference to this section of the site, we created a list of the definitions and of the adopted symbols.