Prerequirements:
- Polynomial functions and polynomials
- Definition of limit of a sequence and of a function
- Calculation of limits in general, Calculation of the limit of the ratio between two polynomial functions
Great part of the study of number theory can be conducted by analizing some concrete cases, that is starting just from numerical calculations. This kind of study supports the development of new ideas and the understanding of some proof techniques, however we have to verify that what observed on numerical basis is true generally, for arbitrarily big numbers. Sometimes this generalization is immediate, other times the tools of a part of mathematical analysis, called asymptotic analysis, are required. Given the importance of this subject for our purposes, we recall some essential elements. The level of mathematical rigour of this post is sufficient for our purposes, but not in general: for a detailed study we encourage you to search in your favourite analysis texts (in our bookshop you can find our recommendations).
The example of polynomials
Let’s consider the functions f(x) = 4 + x^2 and g(x) = x^3. For the first non-negative values of x, they assume the following values:
| x | f(x) | g(x) |
| 0 | 4 | 0 |
| 1 | 5 | 1 |
| 2 | 8 | 8 |
| 3 | 13 | 27 |
| 4 | 20 | 64 |
| 5 | 29 | 125 |
It’s evident that the two functions tend to infinity, as x tends to infinity, and that the function g grows more rapidly than f. In spite of this, the latter has an “initial advantage” that lets it, for x = 0, 1, 2, assume values greater or equal to those ones assumed by the function g. In this case, looking just at the first three rows of the table, you could think the function assuming the biggest values to be f, whereas it’s sufficient to examine the other three rows for realizing that, indeed, the opposite is true.
This situation is even clearer if we consider bigger values of x and plot them. Thus we see that the inizial advantage of the function f can be considered quite insignificant:
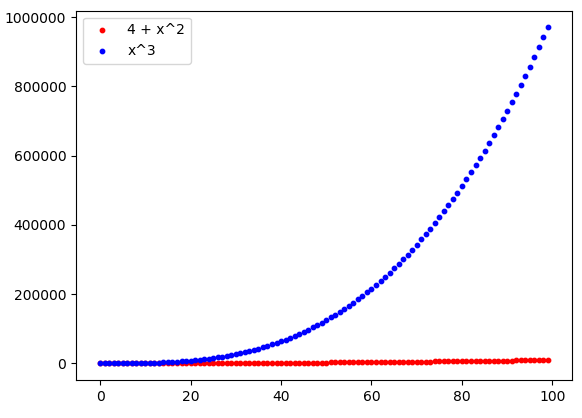
In this context, asymptotic analysis is very important, because it lets know a priori, without any numerical or graphical examination, which out of two functions assumes the greatest values, as x tends to infinity. But this is not enough. A central aspect of this part of mathematical analysis is the definition of orders of infinity and order of infinitesimal. For example, the function f previously defined is an infinity of order 2 because it’s a polynomial function of degree two, whereas g is an infinity of order 3, like its degree. For this reason, according to asymptotic analysis, function g grows more rapidly than f and so, as x tends to infinity, g certainly assumes, from a certain x on (using the terminology of analysis, definitively), greater values with respect to the function f.
Let’s consider now the case of two polynomial functions having the same degree. For example, what does asymptotic analysis say about the comparison between the functions h(x) = 20 + 2 x^2 and i(x) = 4 + 10 x^2? As we saw before, both functions have order of infinity 2. This doesn’t mean that one of the two cannot definitively be greater than the other one, as we can see in the following picture:
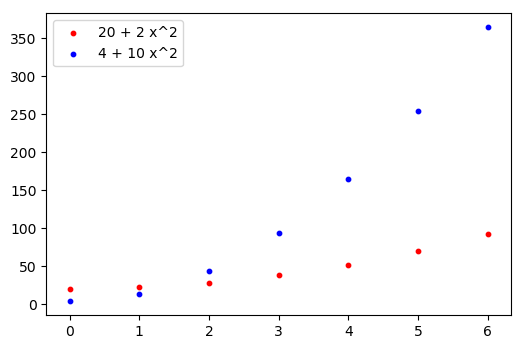
The function with the greatest constant term, h, has a small initial advantage with respect to the function i; in spite of this the latter, as x grows, reveals itself to be definitively greater than the former, due to the presence of a greater coefficient of x^2.
The situations seems similar to that of the comparison between the functions f and g, but there is a substantial difference: this time the faster growth of a function with respect to the other one doesn’t derive from a greater exponent of x, but from a coefficient not depending on x, that is the constant 10. This means that the situation would be overturned by multiplying one of the two functions by an appropriate constant. For instance, if we multiply the function i(x) by \frac{1}{10}, the so obtained function i'(x) = \frac{4}{10} + x^2 is no more asymptotically greater than h(x), but lower, because it has a lower leading coefficient (the “leading coefficient” is the coefficient of the term with the maximum degree).
We can’t say the same thing about the functions f(x) and g(x): no matter how many constants we can try, but we’ll never find one that, when multiplied for example by g, let it be definitively lower than f. Even if, for example, we multiply g by \frac{1}{1.000}, obtaining the function g'(x) = \frac{1}{1.000} x^3, this function would still be definitively greater than f. With a small constant coefficient we have just delayed this event, that can be observed for greater values of x; in any case nothing has changed in the perspective of studying arbitrarily big values of x:
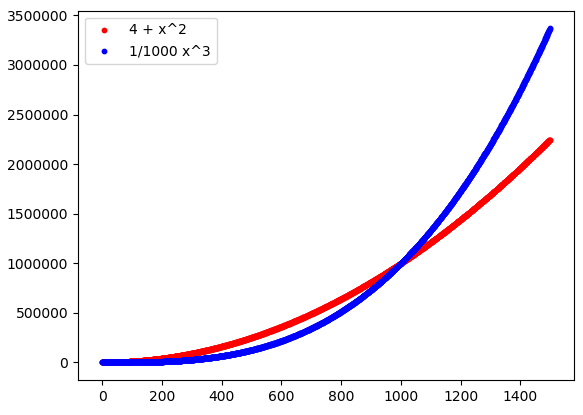
Recapitulating, in the asymptotic comparison between two functions we can distinguish two important cases, listed in the following Definition.
Asymptotic relations “small oh”, “theta”, “big Oh”
Let a and b be two functions defined on a right unbounded subset of \mathbb{R}, with non-negative real values.
- If the function a is definitively lower than b, and this behaviour does not change by multiplying a or b by an appropriate constant, a is said to be a small oh of b, and we write a = o(b) or a \prec b or b \succ a.
- If each of the two functions can become definitively lower or greater than the other one, by the multiplication by an appropriate constant, a and b are said to have the same order, and we write a \asymp b or a = \Theta(b). Equivalently, as in this case the two functions have interchangeable roles, we can also write b \asymp a or b = \Theta(a).
Moreover, if one of the cases above holds, the function a is said to be a big Oh of b, and we write a = O(b) or a \ll b or b \gg a. So
On the whole, functional relationships like a = o(b), a \asymp b and a = O(b) take the name of asymptotic relationships.
In the statement of Definition A.1, it has been pointed out that the two functions must be defined on a right unbounded subset of \mathbb{R}. This is necessary in order to study the behaviour of the functions towards infinity.
For polynomial functions, the cases provided in Definition A.1 can be expressed as reported in the following table:
| General asymptotic relationship | Case of polynomial functions | Example |
|---|---|---|
| a = o(b) | a has a lower degree than b | a(x) = f(x) = 4 + x^2, b(x) = g(x) = x^3 |
| a \asymp b | a and b have the same degree | a(x) = h(x) = 20 + 2 x^2, b(x) = i(x) = 4 + 10 x^2 |
| a = O(b) | a has a lower or equal degree with respect to b | Both the examples above |
Let’s analyze a particular case now.
We have seen that, if two polynomial functions a(x) and b(x) have the same degree, then the one asymptotically greater is that having the greater leading coefficient. But what if the leading coefficient is the same? What can we say for example about the functions a(x) = 1 + x + 2 x^2 and b(x) = 2 + 3x + 2 x^2? As the maximum degree term 2 x^2, which is the “heavier” one going to infinity, is the same, these functions are so similar in asymptotic sense, that can be considered equivalent. Therefore the following definition is given:
Asymptotic equivalence, case of polynomial functions
If two polynomial functions a and b have the same degree and the same leading coefficient, we write
and we read “a is asymptotically equivalent to b“.
Two more general definitions
Up to now we talked about asymptotic analysis by taking the case of polynomials as reference, in fact it’s sufficient for understanding the basic mechanisms. We formulated Definition A.1, which, though, does not mention polynomials: indeed this definition can be applied for generic functions, whereas Definition A.2 holds only for polynomials. Now we bring the generalization begun with Definition A.1 a step further, in order to obtain a new definition that:
- Include both Definition A.1 and Definition A.2;
- Holds also for functions with negative values;
- Is written in such a way to be easily employable into calculations.
We can reach these goals with or without the concept of limit. Let’s see the formulation without limits first and then, who wants can see the other too.
Asymptotic relationships, alternative definitions using inequalities
Let a and b be two functions defined on a right unbounded subset of \mathbb{R}, with real values. Let b be definitively positive.
If there exists a real positive constant A for which definitively
then a is said to be a big Oh of b and we write a = O(b) ot a \ll b or b \gg a. In particular:
- If the inequality (1) holds definitively for all real positive constants A, then a is said to be a small oh of b, and we write a = o(b)
- If there also exists a real positive constant B for which (1) can be extended leftwards with the inequality B b(x) \leq a(x), that is if there exist two real positive constants A and B such that definitively
B b(x) \leq |a(x)| \leq A b(x) \tag{2}
then a is said to have the same order of b and we write a \asymp b or a = \Theta(b). In this case the roles of a and b can be exchanged, therefore also b \asymp a.
- If in particular (2) without absolute value:
B b(x) \leq a(x) \leq A b(x) \tag{2'}
holds definitively for all A \gt 1 and for all B \lt 1, then a is said to be asymptotically equivalent to b and we write a \sim b. In this case, like before, also b \sim a.
As we have seen, a = O(b) can also be written as a \ll b or as b \gg a. The first notation is the most common but sometimes, especially in more advanced contexts, the symbols \ll and \gg are preferable for two reasons:
- They avoid putting parentheses inside expressions. This makes formulas easier to read, especially when the function that should fit inside the big Oh (the b of the Definition) is given by a very long expression.
- They are intuitive, because they remember the minor and major symbols that appear inside the definition of big Oh. For example, a \ll b and a = O(b) both mean that there exists a positive constant A such that definitely |a(x)| \leq A b(x), but with the first notation this aspect is more evident. If you like, you can read the symbols \ll and \gg as “definitely less than, up to a constant factor” and “definitely greater than, up to a constant factor”: these expressions make the idea clear, hiding some often useless details (the absolute value, which is not needed for always positive functions, and the possible equality, which can be eliminated simply by increasing the constant) and other details taken for granted (the positivity of the constant).
Let’s see again the examples we used for introducing the matter, in the light of Definition A.3.
- Considering the polynomial functions f(x) = 4 + x^2 and g(x) = x^3, we have that f = O(g), because we can find a real positive constant A such that definitively |f(x)| = f(x) \leq A g(x), that is 4 + x^2 \leq A x^3. This constant may be simply 1: in fact, as we saw in Figure 1, definitively 4 + x^2 \leq x^3.
- In particular, f = o(g), because in the previous point we could choose, indeed, any constant. In fact, as we saw in Figure 3, even choosing a very small A, still definitively 4 + x^2 \leq A x^3 (this, of course, should be proved in a formal way. If you want to try, let 4 + x^2 \leq A x^3: making the calculations, you will find an x starting from which the inequality is true: in other words, the inequality holds definitively, which is exactly what’s required).
- Considering the polynomial functions h(x) = 20 + 2 x^2 and i(x) = 4 + 10 x^2, we have that h = \Theta(i). In fact we can find some real positive constants A and B such that definitively B i(x) \leq h(x) \leq A i(x), that is B (4 + 10 x^2) \leq 20 + 2 x^2 \leq A (4 + 10 x^2), for example A = 5 and B = \frac{1}{5}:
\begin{aligned}\frac{1}{5} (4 + 10 x^2) \leq 20 + 2 x^2 \leq 5 (4 + 10 x^2) & \iff\\ \frac{4}{5} + 2 x^2 \leq 20 + 2 x^2 \leq 20 + 50 x^2 & \end{aligned}
This inequality is always true and thus, all the more so, it’s definitively true.
- Considering the functions a(x) = 1 + x + 2x^2 and b(x) = 2 + 3x + 2x^2, in order to verify that a \sim b we have to see if the inequality
B (2 + 3x + 2x^2) \leq 1 + x + 2x^2 \leq A (2 + 3x + 2x^2) \tag{3}
holds definitively for all A \gt 1 and all B \lt 1:
- Concerning the constant A, the inequality is rather evident because 1 + x + 2x^2 \leq 2 + 3x + 2x^2 for x \geq 0. So the second part of (3) holds definitively for A = 1 and all the more so for A \gt 1;
- Concerning B, we can rewrite the first part of the inequality as
(2B - 1) + (3B - 1)x \leq 2(1 - B) x^2 \tag{4}
We have to prove that this inequality holds definitively if B \lt 1. In this case the coefficient of x^2, 2 (1 - B), is positive, so the whole right side term is. So we have two polynomials: one on the right, of degree two and always positive, 2(1 - B) x^2, and one on the left, of which we don’t know the sign but we know it’s of degree one, (2B - 1) + (3B - 1)x. Having a lower degree, the left side polynomial is a “small oh” of the other, so the inequality (2B - 1) + (3B - 1)x \leq A 2(1 - B) x^2 holds definitively for all A: in particular it holds definitively for A = 1, that is just (4).
Asymptotic relationships, alternative definitions using limits
Let a and b be two functions defined on a right unbounded subset of \mathbb{R}, with real values. We suppose for simplicity a(x) to be always different from zero. Let
If L exists and is a real number, a is said a big Oh of b and we write a = O(b). In particular:
- If L = 0, a is said small oh of b and we write a = o(b).
- If L = 1, a is said asymptotically equivalent to b and we write a \sim b. In this case the roles of a and b can be exchanged, so also b \sim a.
- If L \neq 0, including the previous case, a is said to have the same order of b and we write a \asymp b or a = \Theta(b). In this case also, like before, b \asymp a.
The case of asymptotically equivalent functions is particularly interesting. By Definition A.4, in this case
If this is true, it means that the functions a and b are completely interchangeable in the calculation of limits. This is particularly important from an analytical perspective: for example in this way a limit involving “difficult” functions can be computed, replacing them with equivalent but “easier” functions.
Definition A.4 is perhaps, among all formal definitions of asymptotic relationships, the most “polite” and concise one; however it has the defect of being applicable only in algebric expressions in which limits have been explicitly introduced. In the other cases it’s worth keeping in mind Definition A.3 also.
For greater clarity, and for future reference, we can summarize Definitions A.1, A.3 and A.4, together with the case of polynomial functions, in the following table. The most willing people can exercise in proving the equivalence of the three definitions; however for our purposes it’s sufficient to remember them, knowing they are equivalent, and to be able to apply them, like we’ll do later.
| Asymptotic relationship (alternative notations) | Equivalent relationship | Definition A.1 | Definition A.3 | Definition A.4 | Case of polynomial functions |
|---|---|---|---|---|---|
| a = O(b) | a = o(b) \textrm{ or } a \asymp b | There exists a real positive constant A for which definitively |a(x)| \leq A b(x) | The limit \lim_{x \to +\infty} \frac{a(x)}{b(x)} exists and it’s a real number | a has a lower or equal degree with respect to b | |
| a = o(b) (a \prec b, b \succ a) | The function a is definitively lower than b, and this behaviour does not change by multiplying a or b by a constant | For all real positive constants A, definitively |a(x)| \leq A b(x) | \lim_{x \to +\infty} \frac{a(x)}{b(x)} = 0 | a has a lower degree than b | |
| a \asymp b (a = \Theta(b)) | b \asymp a (b = \Theta(a)) | Each of the two functions can become definitively lower or greater than the other one, by the multiplication by an appropriate constant | There exist two real positive constants A and B such that definitively B b(x) \leq |a(x)| \leq A b(x) | \lim_{x \to +\infty} \frac{a(x)}{b(x)} \neq 0 and it’s a real number | a and b have the same degree |
| a \sim b | b \sim a | for all A \gt 1 and all B \lt 1, B b(x) \leq a(x) \leq A b(x) | \lim_{x \to +\infty} \frac{a(x)}{b(x)} = 1 | a and b have the same degree and the same leading coefficient |
In number theory we’ll make use of asymptotic analysis in a very particulat context, that is for x tending to infinity and for integer values of x.