Prerequirements:
- The lemma of bar chart area
- Integrals and their properties
- Fundamental theorem of integral calculus
- Continuous functions
- C class of a function
So far we defined and studied only functions defined on integer numbers, the values of which can be integer (like the \theta(x) and \psi(x) functions) or real (like the \theta^{\star}(x) and \psi^{\star}(x) functions). You could think it’s obvious, since our goal is studying integer numbers, in particular prime numbers. However, as it often happens in Mathematics, in order to study a certain class of objects it often turns out to be useful to take inspiration from a wider class, by means of an abstraction process. Thus, in order to study integer numbers, we’ll see that it’s useful to take inspiration from real numbers. This means, in practice, extending the domain of a function from integer numbers to real numbers: a significant jump. Let’s see two ways to do that.
Simple extension
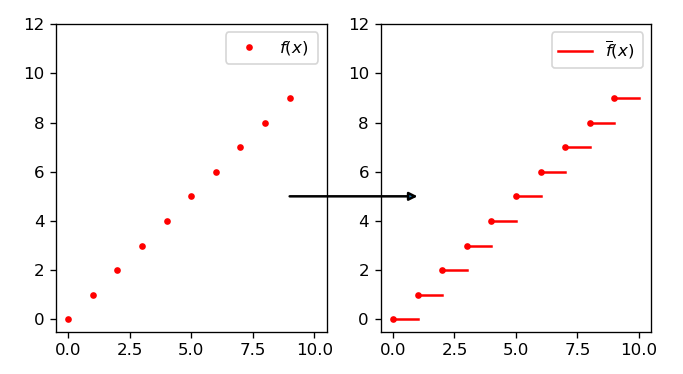
Let’s consider a function f defined on a set of integers I (we suppose in general I \subseteq \mathbb{Z}. Starting from f, we define on positive real numbers a new function \overline{f}, such that:
- For each integer n \in I, \overline{f}(n) = f(n)
- For real numbers greater than n, up to the next integer n + 1 not included, \overline{f} still assumes the value f(n)
If we compare the graphs of the two functions, we can see that function f looks “punctiform”, because the definition set is discrete, whereas function \overline{f} looks “step-like”. For example, with I = \{0, \ldots, 9\} and f(n) = n we have:
The function \overline{f} is defined on a set we can call \overline{I}, obtained from I by adding, for each integer in it, all real numbers up to the next integer excluded. For example:
| I | \overline{I} |
|---|---|
| \{0, 1, 2, 3\} | [0, 4) |
| \mathbb{N} | [0, +\infty) |
| \mathbb{N}^{\star} | [1, +\infty) |
| \mathbb{Z} | \mathbb{R} |
The formal definition of simple extension is the following:
Simple extension of a function defined on integer numbers, to real numbers
Let f: I \rightarrow \mathbb{R} be a function defined on a set I \subseteq \mathbb{Z}. We define on the set \overline{I} := \bigcup_{n \in I} [n, n+1) the function \overline{f}: \overline{I} \rightarrow \mathbb{R} such that:
\forall n \in I\ \forall x \in [n, n+1): \overline{f}(x) := f(n) \tag{1}We’ll call function \overline{f} “simple extension of f to real numbers”, or simply “simple extension of f“.
Formula (1) is the formal translation that \overline{f} assumes the same value as f on any integer n and on the next reals, up to the next integer not included. The same thing can be expressed also with the following equivalent definition:
\overline{f}(x) := \begin{cases} f(x) & \text{if }x \in I \\ f(\left \lfloor x \right \rfloor) & \text{otherwise}\end{cases} \tag{2}This formula says essentially that:
- on integers, i.e. on the set I, f and \overline{f} assume the same value
- on the other real numbers x, \overline{f} assumes the value assumed by f on the integer immediately preceding x, that is the integer part of x
For example, \overline{f}(\frac{7}{2}) is the value assumed by f on the integer part of \frac{7}{2}, that is \left \lfloor \frac{7}{2} \right \rfloor = 3. The same thing happens for all reals in the range [3, 4), because they all have 3 as integer part: repeating this argument with a generic integer n in place of 3, you can understand how (2) is equivalent to (1).
We note that the values assumed by \overline{f} are, on the whole, the same assumed by f: in fact in definition (1) the values of \overline{f} are defined through appropriate values of f. In other terms, the functions f and \overline{f} have the same image: f(I) = \overline{f}(\overline{I}).
We called “simple” the extension described in Definition N.8 not to indicate that’s “easy”, but because, if I is finite, the extension \overline{f} is a so-called “simple function”, that is, simplifying, a function that assumes a finite number of different values. Simple functions are studied in misure theory.
Generic extensions
Definition N.8 may seem artificial: you could think about obtaining the extending function simply by defining it in the same way as f, but on real numbers. For example you could extend the function
f: \mathbb{N} \rightarrow \mathbb{R} \text{ such that } f(n) := nwith the function
\widetilde{f}: \mathbb{R} \rightarrow \mathbb{R} \text{ such that } \widetilde{f}(x) := x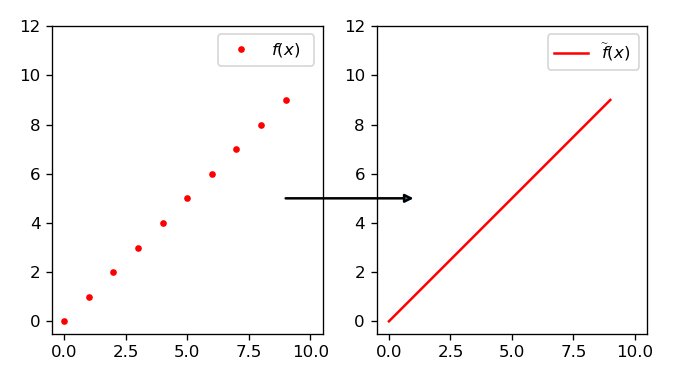
Here the original and the extended function share the same formal expression (we just put x in place of n, but we could also use the same variable name for both cases). However not all expressions that have sense for integer numbers, still do when you pass to reals. For example, a definition like:
g(x) := \text{number of divisors of }xmakes perfectly sense if x is an integer number, but doesn’t for a generic real number (for example, what would the divisors of \sqrt{2} be?). For avoiding this kind of problems, we won’t attempt to formalize the idea of obtaining an extension through a “similar expression” to the one that defines the original function, though this is what happens in most cases. Instead we keep intentionally generic the definition of extension, with the only constraint that the original and the extended function must assume, on the integers, the same values:
Extension by expression of a function defined on integer numbers, to real numbers
Let f: I \rightarrow \mathbb{R} be a function defined on a set I \subseteq \mathbb{Z}. Let \overline{I} := \bigcup_{n \in I}[n. n+1) and \widetilde{f}: \overline{I} \rightarrow \mathbb{R} a function such that:
\widetilde{f}_{\mid I} = fWe’ll say that the function \widetilde{f} is an “extension of f to real numbers”, or simply an “extension of f“.
We can note that simple extension (Definition N.8) is a particular case of extension. In fact by definition \overline{f}(x) = f(n) for all n \in I and for all x \in [n, n+1); in particular, for x := n we have that \overline{f}(n) = f(n).
At a graphical level, we have that the graph of f is made up by isolated points (one point for each n \in I), while the graph of \widetilde{f} is a generic curve that passes through these points. In the case of simple extension (Figure 1), this curve is given by the union of several separate segments: it’s a sign that the extension is not continuous, contrary to the example of Figure 2.
Application to the lemma of bar chart area
In number theory, extensions are often used, because they let apply theorems of real analysis to functions defined on integer numbers. In particular, simple extension is useful when a function defined on integer numbers multiplies an integral, and in that case it lets bring the function under the integral sign.
An example of application of extensions is the Lemma of bar chart area:
A = \sum_{k = 1}^{n-1} C_k (f(k) - f(k + 1)) + C_n f(n) \tag{3}In fact, in the right expression, the summation can be rewritten differently by applying the concept of extension.
First of all, extending the function f we can rewrite the term f(k) - f(k + 1) as \widetilde{f}(k) - \widetilde{f}(k + 1). At this point, assuming the function \widetilde{f} to be of class C^1 on all \overline{I} (so in particular on the interval [k, k+1)), so that its derivative is continuous and so integrable, we can apply the Fundamental theorem of integral calculus, obtaining:
\widetilde{f}(k) - \widetilde{f}(k + 1) = - \int_k^{k+1} \widetilde{f}'(t) dt \tag{4}Here’s explained where integrals arise from in number theory: thanks to the fundamental theory of calculus, a simple difference between two numbers becomes an integral. This passage may seem artificial, but we’ll see that it’s essential for the development of the theory.
Placing (4) into formula (3) of the Lemma, the generic summation term becomes
- C_k \int_k^{k+1} \widetilde{f}'(t) dtThe constants C_k, representing the sums of the bases of the first k bar chart rectangles, depending on k, can be globally considered as a function of k, i.e. we can introduce the function:
C: \{1, \ldots, n\} \rightarrow \mathbb{R} \text{ such that } C(k) := C_kThis function, that simply maps k to the k-th constant, lets us rewrite the generic summation term as
- C(k) \int_k^{k+1} \widetilde{f}'(t) dtNow we can make a simple extension of the function C, rewriting this term as
- \overline{C}(k) \int_k^{k+1} \widetilde{f}'(t) dt \tag{5}At this point we have a function \overline{C} that by (1) is constant over the real range [k, k+1). This lets us bring it under the integral sign, obtaining:
- \int_k^{k+1} \overline{C}(k) \widetilde{f}'(t) dt \tag{6}We can call X the constant value of the function \overline{C} in the interval [k, k+1) and, by the properties of integrals, bring it under the integral sign:
- X \int_k^{k+1} \widetilde{f}'(t) dt = - \int_k^{k+1} X \widetilde{f}'(t) dtWe said that the constant X represents the value assumed by \overline{C} at k, so the left member coincides with (5), but it also represents the value assumed by the same function at all points of the range [k, k+1). These points are just the values assumed by the integration variable t, varying between k and k+1, with the exception of the single point k + 1. So the right integral can be rewritten as:
- \int_{k}^{k+1} \left( \begin{cases} \overline{C}(t) & \text{if }t \in [k, k+1)\\ X & \text{if }t = k+1\end{cases} \right) \widetilde{f}'(t) dt \tag{5'}But inside an integral we can modify the integrated function at a single point without affecting the result, so in place of the unnamed function appearing in (5′), inside round brackets, we can simply employ the function \overline{C}. Doing so, nothing changes in the interval [k, k+1), while it doesn’t matter whether \overline{C}(k+1) is equal to X or not: in any case the final result of the integral doesn’t change. In this way equation (6) is obtained.
Putting (6) in place of the generic summation term in (3), the latter becomes:
A = C(n) f(n) - \sum_{k = 1}^{n-1} \int_k^{k+1} \overline{C}(k) \widetilde{f}'(t) dtExpanding the summation, this formula is rewritten as:
A = C(n) f(n) - \left( \int_1^2 \overline{C}(k) \widetilde{f}'(t) dt + \int_2^3 \overline{C}(k) \widetilde{f}'(t) dt + \ldots + \int_{n-1}^n \overline{C}(k) \widetilde{f}'(t) dt \right)Since all consecutive integral pairs have one end in common and the same integrated function, by the properties of integrals they can be joined into a single integral:
A = C(n) f(n) - \int_1^n \overline{C}(k) \widetilde{f}'(t) dt \tag{7}We have thus obtained a new form of the Lemma of bar chart area. In the next post we’ll see the advantage of adopting this new form in place of the previous one, so justifying the introduction of integrals.
Lemma of bar chart area, second form
Let c_1, c_2, \dots, c_n be non-negative real numbers, with n > 0. Let f: \{1, 2, ..., n\} \rightarrow \mathbb{R} a function, and let \widetilde{f} a C^1 extension of f. Then the area A of the bar chart made up of n rectangles, each with basis c_i and height f(i), given by
A = c_1 f(1) + c_2 f(2) + \ldots + c_n f(n) = \sum_{i=1}^{n} c_i f(i)can be also computed with the formula
C(n) f(n) - \int_1^n \overline{C}(k) \widetilde{f}'(t) dtwhere C: \{1, 2, ..., n\} \rightarrow \mathbb{N} is the function defined by C(k) := c_1 + c_2 + \ldots + c_k = \sum_{i=1}^{k} c_i.
In books about number theory you won’t find our notations for the extended functions, like \overline{C} and \widetilde{f}: they are notations introduced by us, not universal. Normally no specific notation is used to distinguish the extended functions from the respective original functions, for example (7) would be written as follows:
A = C(n) f(n) - \int_1^n C(k) f'(t) dtHowever we think it’s worth distinguishing, for better clarity, between functions that “are born” defined only on integer numbers, and their real extensions. Moreover the notation we chose for simple extensions, like \overline{C}, thanks to the horizontal line sign, helps to remember that it’s a “step-like” function, contrary to generic extensions, that are normally continuous functions.