Prerequirements:
- The functions W and V
- Chebyshev’s Theorem (strong version)
- From integer numbers to real numbers – second part
In the previous post we saw that a sufficient condition for proving the Prime Number Theorem is the following:
While our starting point, that is what we know about the function V thanks to Chebyshev’s Theorem, is the following:
So we asked ourselves if (2) implies (1). Well, the answer is yes, but the proof is not as simple as it may seem. In fact equations (1) and (2) both say something about the function V, but in quite different ways:
- (1) considers a single value of V, so it analyses the behaviour of V in a single point \log x (though this point is not fixed, but it’s variable as an effect of the limit superior); instead (2) takes into consideration the integral of V, which is computed from many values of the functions at the same time, in particular from all the values u such that 0 \leq u \leq \log x.
- (1) considers the function V inside the absolute value; (2) does not.
The difference concerning the absolute value is indeed a minor problem, because the absolute value is easily insertable or erasable with appropriate algebraic techniques. For example, in the previous post we introduced it in order to obtain a single equation, which is (1), instead of two different equations. Similarly, in due time we’ll introduce it by appropriate techniques also into (2). For the moment we can neglect this aspect and assume the absolute value is already there, even if we don’t know how the right part of the inequality would change:
For the moment the unknown on the right has no importance, because the main problem is another: it consists in the first difference we found before between (1) and (2). In fact, the value of the function |V| in a point u, given by (1), is an object essentially different from the integral of the same function in an interval, given by (2′), even if that interval contains u. From a graphical point of view, in the first case we’re considering the ordinate of a point in the function graph; in the second case we’re calculating the area below the same graph along a certain interval.
Now, since we have to prove that the function tends to zero, we’re not interested to areas, but to the values assumed by the function; so we have to find a way to transform the integral into a punctual value. Such a way is offered by a classical theorem of analysis, the Mean value Theorem for integrals, which for the sake of convenience we write below:
NODESCR
Let [a, b] be a real interval and f: [a,b] \rightarrow \mathbb{R} be a continuous function. Then there exists c \in [a, b] such that:
In other terms, this Theorem states that the area below the graph of a continuous function f along an interval [a, b] is equal to the area of a rectangle having as its basis the interval width, and as its height a particular value assumed by the function in the interval. Such a value is called “mean value of f on [a, b]” (or “integral mean of f on [a, b]“), because, if it was assumed constantly by the function along all the interval, the value of the its integral would not change. In that sense, it’s a value which balances out the lowest and the highest values assumed by the function along the interval, as you can see in Figure 1.
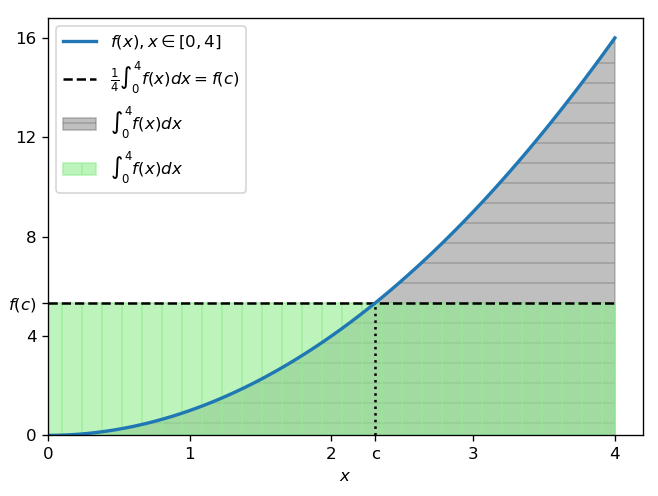
Comparing (3) with (2), it’s clear that, in order to apply the Theorem to our case, we should set a := 0, b := \log x, x := u and f := |V|. But it’s a pity that the Theorem cannot be applied, because one fundamental hypothesis is not satisfied: the continuity of the function. In fact, as we saw in the previous post, the function V has many discontinuities, so, being x arbitrary, we cannot guarantee that it has no discontinuity in the interval [0, \log x]. Though, we can recover from the Theorem a fundamental idea. In fact, if we divide (3) by b - a we’ll obtain:
So we have transformed the integral of the function f into a value assumed by the function itself: it’s exactly what we wanted to do for the function |V|. We can note that the left side expression does not depend on the continuity of f but, in order to make it well defined, it’s sufficient that f is integrable (we recall that a function may be integrable but not continuous, just like our f that is |V|). So we can borrow from the Theorem the idea to calculate that expression, which, after the substitutions listed before, becomes in our case:
Since we cannot apply the Theorem, this value is not necessarily equal to the value assumed by the function in a certain point c, but maybe this c does not exist at all, i.e. the value computed by (4) is indeed never assumed by the function. But this is not important for us: even in such a case, the computed value would still represent a mean of the function values along the interval, so it would still be comparable with them.
Now, since (4) is a quantity which varies as x changes, we can compute its limit superior, which we’ll call \beta:
So we have obtained a quantity which is directly comparable with the left part of (1), which we’ll call \alpha:
In fact, as we said before, the expression \frac{1}{\log x} \int_0^{\log x} |V(u)| du that appears in (5) represents the mean value of the function |V| on the interval [0, \log x], and, being such, it’s meaningful to compare it with the value |V(\log x)| which appears in (6), even if the mean value does not match any value assumed by the function.
Summarizing, we have defined two constants:
Constants \alpha and \beta
Given the integer variable x \gt 0, we define the following constants:
The constants \alpha and \beta so defined are real numbers, i.e. we can exclude that \alpha = +\infty and that \beta = +\infty. This property is important, because in the continuation of the proof we’ll need to use these constants in algebraic calculations, and it follows directly from the boundedness of the function |V| (Proposition N.7A):
\alpha and \beta are real
The constants \alpha and \beta defined by Definition N.14 are real numbers.
By Proposition N.7A, the function |V| is bounded, so there exists a real number A such that |V(u)| \leq A for all u. Then \alpha = \limsup_{x \to +\infty} |V(\log x)| \leq \limsup_{x \to +\infty} A = A, hence \alpha \leq A; in particular, \alpha is real.
Concerning \beta, we can reason in the same way: \beta = \limsup_{x \to +\infty} \frac{1}{\log x} \int_0^{\log x} |V(u)|\ du \leq \limsup_{x \to +\infty} \frac{1}{\log x} \int_0^{\log x} A\ du = \limsup_{x \to +\infty} \frac{1}{\log x} A \log x = \limsup_{x \to +\infty} A = A, hence \beta \leq A: in particular, \beta is real.
Now we can introduce the fundamental question of the Prime Number Theorem proof: what relationship connects \alpha and \beta? The proof will be based on this question. In fact, as we recalled initially, we want to prove (1), that is equivalent to \alpha = 0. On the other hand, \beta cannot be negative, because, in (5), |V(u)| cannot be negative, as well as its integral mean value, and the limit superior of its integral mean value, which is just \beta. So certainly we’ll have to prove that \alpha \leq \beta: this will be our goal in the next posts. Let’s explicit it, starting from (5) and (6):
The first thing that you may ask yourself when looking at (7) is if the same relationship is true without the limit superior, that is:
where the role of x has changed: from being the integer variable used for the calculation of the limit superior, it has become a fixed positive integer. So in (8) the value |V(\log x)| is compared with a mean value computed from all the previous values of the function |V|.
Now we just have to make some calculations, in order to simplify (8). In fact, in the left member there is the expression V(\log x) which can be easily simplified, as the function V is defined by an exponential function, that can be simplified with the logarithm:
We could make similar passages on the right member, but we want to do something more sophisticated. Our goal is not only simplifying the logarithm with the exponential, but also passing from a relative error, given by the function W, to an absolute error, represented by its numerator, that from now on will be for us a function on its own, called R, the graph of which is shown in Figure 2:
Function R
We define the following function R: [1, +\infty) \rightarrow \mathbb{R}:
for all t \in [1, +\infty).
By combining the definition of the function R with the one of the function V (Definition N.13), we’ll obtain that:
for all u \in (0, +\infty). In fact, V(u) = W(e^u) = \frac{\overline{\psi}(e^u) - e^u}{e^u} = \frac{R(e^u)}{e^u}. Thus we have isolated the absolute error function R within the function V.
By applying Definition N.15, (9) can be rewritten as follows:
In order to simplify the integral on the right in (8), more complex passages are necessary instead, after which we’ll obtain:
By applying (10), we’ll have that \int_0^{\log x} |V(u)| du = \int_0^{\log x} |\frac{R(e^u)}{e^u}| du. Now the idea is again to simplify the exponential with the logarithm. For doing that, we could make the substitution t := e^u, but, by making some calculations, we would realize that there is another more convenient substitution: t := \frac{x}{e^u}. With this substitution, first of all the integration ends change as follows:
- The lower end changes from 0 to x, because u = 0 \Rightarrow \frac{x}{e^u} = \frac{x}{1} = x
- The upper end changes from \log x to 1, because u = \log x \Rightarrow \frac{x}{e^u} = \frac{x}{x} = 1
Moreover dt = d\left ( \frac{x}{e^u} \right ) = -\frac{x}{e^{2u}} e^u du = -\frac{x}{e^u} du = -t du, hence du = -\frac{1}{t} dt. All that considered, we’ll have:
Where, in the passage from the fourth to the fifth line, we used the fact that \left|\frac{t}{x}\right| = \frac{t}{x}, since the fraction is positive because both t and x are; moreover in the last passage we were allowed to bring \frac{1}{x} out of the integral because that expression does not depend on the integration variable t. Finally, renaming t to u in the last expression (forgetting how we obtained it), we’ll obtain (12).
By putting (11) and (12) into (8), we’ll have that:
In the last passage we can note the simplification of \frac{1}{x}, that finally removes the denominator from \frac{R(x)}{x}, thus passing from a relative error to an absolute error (for who read the detailed part, this passage is the reason why in the integral we made the substitution t := \frac{x}{e^u} instead of the simpler one t := e^u).
Thus we obtained the following Lemma:
NODESCR
Let x \gt 0 be a fixed integer. The following inequalities are equivalent:
- |V(\log x)| \leq \frac{1}{\log x} \int_0^{\log x} |V(u)| du
- \log x |R(x)| \leq? \int_1^x \left|R\left(\frac{x}{t}\right)\right| dt
Summarizing, we can state the following Hypothesis:
Hypothesis about the relationship between \alpha and \beta expressed through the absolute error function R
Given a fixed integer x \gt 0 and the constants \alpha and \beta defined in Definition N.14, we suppose that the relationship \alpha \leq \beta is true without the \limsup, that is:
Or equivalently, by Lemma N.8:
So, in order to study Hypothesis N.1, we have to find a relationship that connects \log x |R(x)| and \int_1^x |R(\frac{x}{t})| dt. Just to start, we can simplify by replacing the integral by a summation, introducing at the same time some coefficients a_n which will be chosen appropriately in order to obtain a quantity similat to the integral: \sum_{n = 1}^x a_n |R(\frac{x}{n})| (this is an evolution of the approach we saw here: From integer numbers to real numbers: second part). Selberg, the mathematician whom we talked about in the post The Prime Number theorem: history and statement), discovered an asymptotic relationship between the term with logarithm and this kind of summation, both without the absolute value, We’ll call this relationship Selberg’s Theorem:
Selberg’s Theorem
But how can the choice of the coefficients a_n := \Lambda(n) be motivated? For understanding that, we first have to open a long parenthesis, on which we’ll be committed in the next three posts. We’ll temporarily forget the proof passages that we made till now, and then we’ll turn back and see the proof of Selberg’s Theorem and its use.