Prerequirements:
- End of the first part of the proof: the relationship between α and β’
- Selberg’s Theorem: proof and application
- The functions W and V
- Properties of asymptotic orders
- The limit inferior and the limit superior of a sequence
- Elements of asymptotic analysis
In this post we’ll see what are the basic ideas of the second part of the prime number Theorem proof. Up to now we proved that \alpha \leq \beta^{\prime}, where \alpha and \beta^{\prime} are two important constants connected with the function V. As we saw, if we proved that \alpha = 0 we would have proved the prime number Theorem. In order to prove that, a first idea may be proving that \beta^{\prime} = 0, because it would follow that \alpha \leq \beta^{\prime} = 0, hence \alpha = 0. In this post we’ll try to prove that \beta^{\prime} = 0 (and we’ll see why for the moment it will remain just a trial).
First of all, let’s remember the definition of \beta^{\prime}:
So we want to prove that:
For the moment, let’s ignore the limit superior and let’s try to go to the core question: surely, the function of which the limit superior is computed must become very small as \xi increases; otherwise the limit superior could not be zero. But what does “very small” be? In order to specify this expression better, we can fix some real number \epsilon \gt 0 which we regard to be very small: thus “very small” means “less than \epsilon“.
So, we’ll try to prove that:
where \epsilon \gt 0 is a positive real number, fixed a priori, which should be as small as possible. The last inequality can be rephrased as follows:
This simple algebraic passage is very important from a conceptual point of view, because it lets us look at the problem in geometrical terms: in fact, (3) means that the area between the graph of the function |V| and the horizontal axis, between 0 and \log \xi, is less than \epsilon \log \xi.
But the quantity \epsilon \log \xi in turn can be seen as an area: in fact it corresponds to the area of a rectangle having \log \xi as basis and \epsilon as height. So formula (3) represents a comparison between the area below the graph of the function |V| and the area of a rectangle:
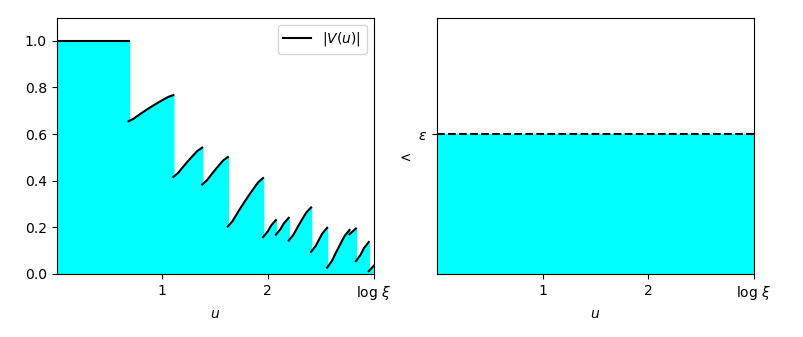
So, how to make the left area smaller than the right one, provided that \epsilon should be as small as possible? In order to answer this question, we’ll illustrate four main ideas.
First idea: start with an overestimation with the absolute value outside of the integral
Just to start, we’ll note that things get simpler if we bring the absolute value outside of the integral. In fact, the following Proposition can be proved:
Overestimation of the absolute value of the integral of V between 0 and a positive number
There exists a real number A \gt 0 such that, for all \xi \gt 0:
In the post The functions W and V, we already proved the following formula (numbered (4′) in the cited post):
Indeed, looking at its proof again, we can note that the argument is still valid when considering a positive real value \xi instead of the integer x:
By Definition A.3, the last asymptotic equality means that there exists a positive constant B such that \left| \int_0^{\log \xi} V(u)\ du \right| \lt B definitively, i.e. for all \xi greater or equal to a fixed \xi_0. So, in order to prove Proposition N.24, we have to prove that also for \xi \lt \xi_0 a similar relationship is true.
By Proposition N.7A, the function |V| is bounded, i.e. there is a constant C such that V(u) \leq C for all u. Then \left| \int_0^{\log \xi} V(u)\ du \right| \leq \left| \int_0^{\log \xi} C\ du \right| \leq \left| C \log \xi \right| = |C| \log \xi. So, since the logarithm is increasing, for \xi \lt \xi_0 we’ll have that \left| \int_0^{\log \xi} V(u)\ du \right| \leq |C| \log \xi \lt |C| \log \xi_0.
Ultimately, considering both the case \xi \geq \xi_0 and the case \xi \lt \xi_0, we’ll have that \left| \int_0^{\log \xi} V(u)\ du \right| \lt \max(B, |C| \log \xi_0). Now Proposition N.24 can be obtained by setting A := \max(B, |C| \log \xi_0).
The problem of this Proposition is that the absolute value is outside of the integral. In practice, here the integral computes the areas between the graph of the function V and the horizontal axis with the sign, i.e. those ones below the horizontal axis with positive sign, and those ones below it with negative sign:
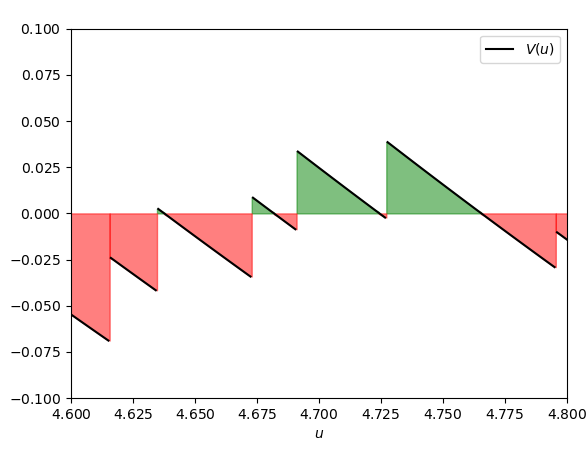
So, the integral \int_0^{\log \xi} V(u)\ du is given by the result of the subtraction of negative areas from positive ones. Therefore, the only effect of the absolute value in Proposition N.24 is that, if the result of that operation were negative (like in the figure above, in which negative areas are visibly greater than positive ones), the absolute value would turn it into a positive number.
Instead, if the absolute value were inside the integral, then negative areas would be overturned, so they would be considered as positive areas:
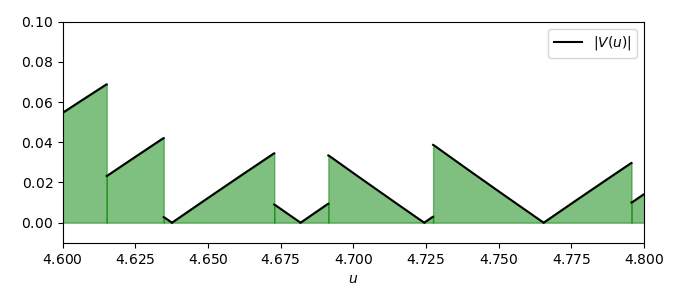
It’s clear that in this case the final area is greater than before, because now all areas have positive sign. This explains the difficulty of using Proposition N.24 for proving (3): even if we were successful in proving that \left| \int_0^{\log \xi} V(u)\ du \right| \lt \epsilon \log \xi, the expression we are interested in, \int_0^{\log \xi} |V(u)|\ du, may be greater than \left| \int_0^{\log \xi} V(u)\ du \right| and so also greater than \epsilon \log \xi, frustrating our effort.
But there is a particular case in which Proposition N.24 can be really useful: we can use it as long as the function V does not change sign. Indeed, as you can see in Figure 2 of the post The functions W and V, initially the function V is always negative, so if our \xi is not too big we’ll have that:
Let’s suppose that \xi is enough small so that V is always negative between 0 and \log \xi. Then:
But the integral \int_0^{\log \xi} V(u)\ du cannot be positive, because V is negative in all the integration interval, so:
Joining the two previous formulas, we can obtain (4).
so, by Proposition N.24:
If this relationship is true, then also (3) is true, provided that
But A and \epsilon are fixed, while \xi is variable, so A can be made lower than \epsilon \log \xi by choosing a value of \xi big enough. However, we have to further investigate this issue, because it’s not sure that, up to this \xi big enough, the function V is always negative, as formula (4), from which we started, would require.
Second idea: divide into smaller intervals
Now the second idea comes into play. If we divide the interval [0, \log \xi] into smaller intervals, we can study each of those intervals separately, with the advantage that we can choose the ends of the intervals as we like; the only constraint is that the first interval must start with 0 and the last one must end with \log \xi.
So, generally we can suppose to have a sequence of intervals of the kind [0, t_1], [t_1, t_2], [t_2, t_3], \ldots, [t_n, \log \xi], with 0 \lt t_1 \lt t_2 \lt t_3 \lt \ldots \lt \log \xi, where t_1, t_2, t_3, \ldots, t_n are convenient points, of our choice, of the interval [0, \log \xi] (and also n is of our choice). To each of these intervals we can apply the following Corollary of Proposition N.24:
Overestimation of the absolute value of the integral of V between two positive or null numbers
There exists a real number A \gt 0 such that, for all a \geq 0 and for all b \gt a:
If a = 0, then it will be sufficient to apply Proposition N.24 making sure that \log \xi = b, i.e. setting \xi := e^{b}.
If instead a \gt 0, we’ll have that:
where in the last inequality we applied Proposition N.24.
We wanted to highlight that the constant A which appears in this Corollary is the same of Proposition N.24, by using the same symbol. As an alternative, we could have set B := 2A and state the Corollary as follows:
There exists a real number B \gt 0 such that, for all a \geq 0 and for all b \gt a:
This Corollary overcomes the limitations of Proposition N.24 because, whereas previously we had to suppose the function V to be always negative between 0 and \xi, now we can choose the intervals as we prefer, so we can choose any interval in which the function V is always negative. If [a, b] is such an interval, by a proof similar to the one of (4) we’ll have that:
hence
Furthermore, we can also treat the opposite case. In fact, formulas (4′) and (5′) are still valid if we choose an interval [a, b] in which V is always positive.
Why are formulas (4′) and (5′) still valid if V is always positive in the interval [a, b]?
In this case the proof is simpler than the one for the negative case, because, if in the interval [a, b] the function V is always positive, then in the integral \int_{a}^{b} |V(u)|\ du we’ll have that |V(u)| = V(u), so the integral is equal to \int_{a}^{b} V(u)\ du and it assumes a non-negative value, because \forall u \in [a, b]: V(u) \gt 0 \Rightarrow \int_{a}^{b} V(u)\ du \geq \int_{a}^{b} 0\ du = 0. Then both the integrals \int_{a}^{b} |V(u)|\ du and \int_{a}^{b} V(u)\ du coincide with their absolute value, so \int_{a}^{b} |V(u)|\ du = \int_{a}^{b} V(u)\ du = \left| \int_{a}^{b} V(u)\ du \right|.
So we can state the following Lemma:
Overestimation of the integral of V in the intervals in which it doesn’t change sign
Let [a, b] be an interval in which the function V is always positive or always negative. Then there exists a positive constant A such that:
If this argument were taken to the extreme, whatever \xi is, we could divide the interval [0, \xi] into all and only the sub-intervals in which the function is either always positive or always negative, by changing interval as soon as the function changes sign.
Looking at the graph of the function V (see Figure 2), we can note that it’s composed of a sequence of continuous and decreasing segments. So there are only two ways in which the function can change sign while we move towards right:
- A continuous and decreasing segment crosses the horizontal axis at a point t: in this case t will be the end of an interval and the start of the next one.
- A continuous and decreasing segment in which the function is negative is followed by another one in which the function is positive, and between the two there is a discontinuity at a point t, belonging to one of the two segments: also in this case t will be the end of an interval and the start of the next one.
So, the construction works as follows:
- we locate the points in which the function V is 0 or has a discontinuity;
- we break the interval [0, \log \xi] at such points, obtaining a sequence of intervals of the kind [0, t_1], [t_1, t_2], [t_2, t_3], \ldots, [t_n, \log \xi].
Since in each such interval the function has always the same sign, setting t_0 := 0 and t_{n+1} := \xi, by (5′) we’ll have:
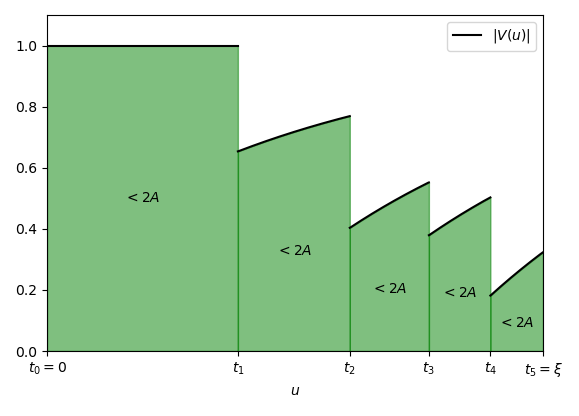
Now let’s suppose that the size of the i-th interval, t_{i+1} - t_i, is big enough to have that 2A \lt \epsilon (t_{i+1} - t_i), where \epsilon is the constant we fixed initially. Then we’ll have that:
Now, summing up for all indexes i, and considering that the sum of all the interval sizes is \log \xi, we’ll have that:
This way we could prove (3). The problem is that the hypothesis 2A \lt \epsilon (t_{i+1} - t_i) certainly cannot be true for arbitrarily small values \epsilon: the smaller \epsilon is, the biggest t_{i+1} - t_i should be; but this quantity cannot be as big as we want, because it’s fixed, since it’s constrained by where the zeroes and the discontinuity points of V are located. The next idea can help us to overcome this problem.
Third idea: study how the absolute value of V increases after a zero
The previous idea consisted in dividing the interval [0, \log \xi] into the sub-intervals [0, t_1], [t_1, t_2], [t_2, t_3], \ldots, [t_n, \log \xi], in such a way that, for all i = 1,\ldots,n, t_i is a discontinuity point of V or a zero of V. Now let’s focus our attention on the last case: if V(t_i) = 0, what happens in a neighbourhood of t_i? Maybe the function V, at points near t_i, assumes values close to zero, or which at least can be bounded somehow. For example, let’s suppose to find some function which bounds the growth of |V| in the neighbourhood of one zero of it, i.e. a positive function f such that, for all h \geq 0, |V(t_i + h)| \leq f(h):
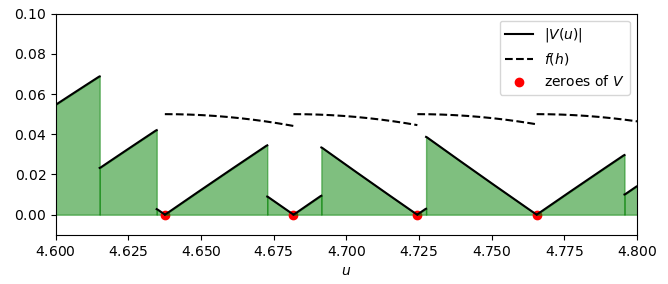
Then:
Now, if the function f in the interval [t_i, t_{i+1}] were always less than or equal to \epsilon, we would have that:
So we would have obtained the same result as (6), but through another path. The advantage in this case is that, after we found a zero of V, in one neighbourhood of it we don’t make any hypothesis on V; whereas previously we required it to have constant sign, so we were forced to choose the ends of intervals in a particular way.
Indeed it’s possible to proceed in the described way, thanks to the following Proposition:
Overestimation of the absolute value of V after one zero of it
Let t be a zero of V. Then, for all h \geq 0:
By hypothesis, V(t) = R(e^t) = 0. So we can rewrite the number |V(t + h)| as follows:
This way, at the numerator we obtained two terms of the kind R(\xi) \log \xi, with \xi \gt 0, which recalls the first term of Selberg’s Theorem. In fact, if in that Theorem we consider the real variable \xi instead of the integer variable x, we’ll obtain the following statement:
In the post Selberg’s Theorem: proof and application, in particular in formula (5), we saw that \sum_{n \leq x} \Lambda(n) R\left( \frac{x}{n} \right) = \sum_{nm \leq x} \Lambda(n) \Lambda(m) - x \log x + O(x). Maintaining the convention that \sum_{n \leq \xi} := \sum_{n \leq \left \lfloor \xi \right \rfloor}, we can substitute the last equality into (b):
hence, by applying Corollary of Property A.9, we’ll obtain:
Now, substituting first \xi := e^{t + h} and then \xi := e^t, and finally subtracting side by side, we’ll obtain:
But the summation cannot be negative, because \Lambda is a non-negative function, so:
Considering that h is constant and by applying in sequence the Properties A.5, Corollary of Property A.7, A.16, A.10, Corollary of Property A.9 e A.11, we’ll have that O(t + h) = O(O(t) + O(1)) = O(O(t) + o(t)) = O(O(t) + O(t)) = O(O(t)) = O(t). Substituting, and applying the Properties Corollary 3 of Property A.8 and Corollary of Property A.9, we’ll obtain finally:
Substituting into (a), we’ll obtain:
The second term inside the absolute value can be rephrased as follows:
where the passage (*) can be justified by observing that \left| \frac{h}{t + h} \right| = \frac{h}{t + h} \leq \frac{h}{t}, hence, according to Definition A.3, \frac{h}{t + h} = O\left( \frac{1}{t} \right); moreover in the final passage we applied Corollary 3 of Property A.8.
Concerning the third term inside the absolute value in (c), we’ll have:
where:
- In the first passage we applied Corollary I of Property A.8.
- The central passage is a consequence of the equality \lim_{t \to +\infty} \frac{t}{e^{t+h}(t + h)} / \frac{1}{t} = \lim_{t \to +\infty} \frac{t^2}{e^{t+h}(t + h)} = 0 because in the fraction \frac{t^2}{e^{t+h}(t + h)} there is an infinity of order two at the numerator, and an infinitely big infinite (exponential function) at the denominator; so, by Definition A.4, \frac{t}{e^{t+h}(t + h)} = o\left( \frac{1}{t}\right).
- In the subsequent passage we applied Properties A.16 and A.10.
Substituting (d) and (e) into (c), and applying Corollary of Property A.9, we’ll obtain:
hence
where in the last passage we applied Property A.6 and we observed that, since h \geq 0, e^h \geq 1 \Rightarrow \frac{1}{e^h} \leq 1 \Rightarrow 1 - \frac{1}{e^h} \geq 0.
The function f in this case is f(h) = 1 - \frac{1}{e^h}, with an error of O\left(\frac{1}{t}\right) (so such an error tends to zero as t tends to infinity).
Fourth idea: if \epsilon \geq \alpha^{\prime}, we can expand an interval as much as we like
The previous ideas were important, but the one we’ll illustrate now will really make the difference. Let’s suppose that, by means of one of the previous techniques, we were able to find an interval [a, b] \subseteq [0, \log \xi] such that:
Both in the first and in the second idea, though, the interval [a, b] had to be big enough to satisfy a relationship of this kind, but at the same time could not be arbitrarily big, being constrained by the zeroes and the discontinuity points of V. But if we suppose that \epsilon \geq \alpha^{\prime}, then there is a very simple way to overestimate the integral of |V| in an interval wider that [a, b], let’s say [A, B], with A \leq a \lt b \leq B, still contained into [0, \log \xi]. This way consists in breaking the interval [A, B] into three parts:
In the first and in the last part we can overestimate the integral of |V| by using a consequence of the definition of \alpha^{\prime}. Since \alpha^{\prime} is the limit superior of the function |V|, by Property A.18 this function is overestimated in all its domain by \alpha^{\prime} up to an infinitesimal error, i.e.:
Since this relationship is valid for all u \in [0, +\infty), it’s even more valid for all u \in [A, a] and for all u \in [b, B], hence:
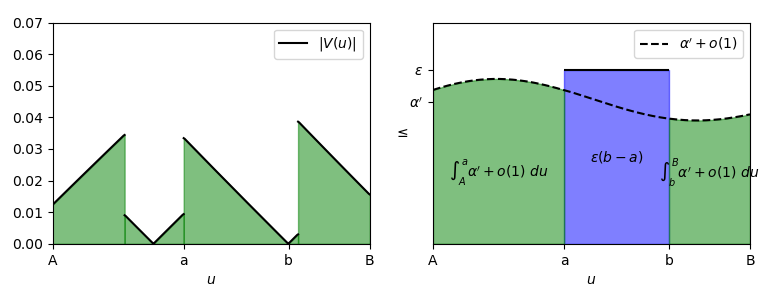
So, by (7) and (8):
Simplifying, the first inequality of (8) becomes:
Now we’ll prove that \int_A^a o(1)\ du = o(1). By Definition A.4, the symbol o(1) stands for a function that tends to zero. So we have to prove that the integral \int_A^a o(1)\ du tends to zero. But tends to zero with respect to what? We have to recall that the variable of the asymptotic notations of our formulas is always \xi, the upper bound of the interval [0, \xi] we are considering, therefore the limit must always be calculated as \xi \to \infty. However in this case we don’t have an expression explicitly involving \xi, but we do have A and a; we must remember, however, that [A, a] \subseteq [A, B] \subseteq [0, \log \xi]; therefore, if \xi tends to infinity, then A and a can also tend to infinity. However A and a are not free variables, but they are linked by the relation A \leq a, so it suffices to let A tend to infinity and set a := A + h, where h represents the width of the interval, which is constant because it is established a priori. Hence the meaning of equality
is:
Now that we’ve cleared that up, we can move on to the actual proof. By definition of limit, it is a question of proving that, for each \lambda \gt 0, \left| \int_A^{A + h} o(1)\ du \right| \lt \lambda for A large enough. Now we can observe that the integrand function o(1) tends to zero (with respect to \xi, therefore also with respect to A), so for each \tau \gt 0 we’ll have that |o(1)| \lt \tau for A large enough. So, for A large enough:
and this quantity can be made less than \lambda by setting \tau \lt \frac{\lambda}{h}, concluding the proof.
If we now suppose that \epsilon \geq \alpha^{\prime}, by (9) we’ll have:
Ultimately, starting from (7), we made an overestimation of the integral on an interval wider than the initial one, making an infinitesimal error.
Change of strategy: set \epsilon := \alpha^{\prime}
The last idea can disrupt the initial argument, because \epsilon should be as small as possible, whereas later we supposed it to be greater or equal to \alpha^{\prime}, which is a constant not known a priori. Given that \alpha^{\prime} cannot be negative, because it’s defined as the limit superior of a non-negative function, we can distinguish two cases:
- If \alpha^{\prime} = 0 there is no problem, because the condition \epsilon \geq \alpha^{\prime} = 0 does not prevent \epsilon from being as small as we want;
- If \alpha^{\prime} \gt 0, the condition \epsilon \geq \alpha^{\prime} is in contradiction with the condition that \epsilon is arbitrarily small, because of course \epsilon could not assume any value between 0 and \alpha^{\prime}.
In the second case, however, we can change our strategy for achieving our final goal, that is to prove that \alpha = 0. In fact, we can reason as follows:
- We already proved, in the previous post, that \alpha \leq \beta^{\prime};
- Modifying the proof, we could prove that also \alpha^{\prime} \leq \beta^{\prime};
- If \alpha^{\prime} \gt 0, we can set \epsilon := \alpha^{\prime} (legitimate operation, because \epsilon must be positive and \alpha^{\prime} is a real number);
- Doing so, by means of the same techniques which would let us prove that \beta^{\prime} \lt \epsilon, we could prove that \beta^{\prime} \lt \alpha^{\prime};
- The points 2 and 4, once proved, would be in contradiction between themselves, so the hypothesis \alpha^{\prime} \gt 0 cannot be true: it must be \alpha^{\prime} = 0;
- If \alpha^{\prime} = 0, by Property N.24 also \alpha = 0, hence, by Lemma N.7, the prime number Theorem would be proved.
So the only open points in order to complete the proof are 2 and 4.
Point 2 would be solved by interpreting x, in the previous post, as a real number instead of an integer number. Many times, during this path, we saw that the passage from integer numbers to real numbers is complicated; but in this case the required changes are minimal. In fact, it’s sufficient to review Selberg’s Theorem: as we noted inside the proof of Proposition N.8, this Theorem is true also if x is real, and the proof remains substantially the same: it’s sufficient to interpret the summations of the kind \sum_{n \leq x}, with real x, as \sum_{n \leq \lfloor x \rfloor} (actually, if x is real, the summation \sum_{n \leq x} is just defined as \sum_{n \leq \lfloor x \rfloor}). So, the proof of the inequality \alpha^{\prime} \leq \beta^{\prime} has no substantial innovation; its usefulness would be above all to review the previous proofs. So we’ll just state the following Proposition, leaving its proof to the most willing students:
Relationship between \alpha^{\prime} and \beta^{\prime}
With reference to Definition N.23:
Point 4 instead requires further details: it’s about putting altogether the ideas illustrated in this post in order to prove that, if \alpha^{\prime} \gt 0, \beta^{\prime} \lt \alpha^{\prime}. This will be the subject of the next post.