Prerequirements:
In this post we’ll see two concepts of mathematical analysis which will be useful in number theory: the limit inferior (\lim \inf) and the limit superior (\lim \sup) of a sequence.
Like for the post about asymptotic analysis, we don’t claim to cover the topic in depth, but out intent is rather to give an intuitive idea of what the limit superior and the limit inferior of a sequence are, without neglecting the mathematical rigour.
Sequences and intervals
Let’s consider a real sequence (a_n)_{n \geq 0} = a_0, a_1, a_2, \ldots, a_n, \ldots, that is a sequence where all the a_n are real numbers. Indeed it’s a function from \mathbb{N} to \mathbb{R} that maps n to a_n, so we can represent it in a Cartesian plane where n is on the horizontal axis and a_n on the vertical axis, like in Figure 1.
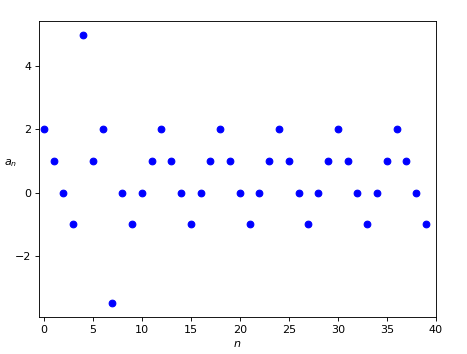
The sequence shown in Figure 1 is given by the following mathematical definition:
Without discussing the details of the algebraic expression of the last case, that in this context has little importance, it’s clear that the cases n = 4 and n = 7 are treated as exceptions; hence we can imagine that, continuing on the right towards infinity, the graph will always have the same behaviour, oscillating between the values -1 and 2. So we can identify two intervals on the vertical axis, which correspond to two horizontal bands in the graph (Figure 2):
- The interval [-\frac{7}{2}, 5], that contains all the terms of the sequence
- The interval [-1, 2], that contains all the terms of the sequence, except two
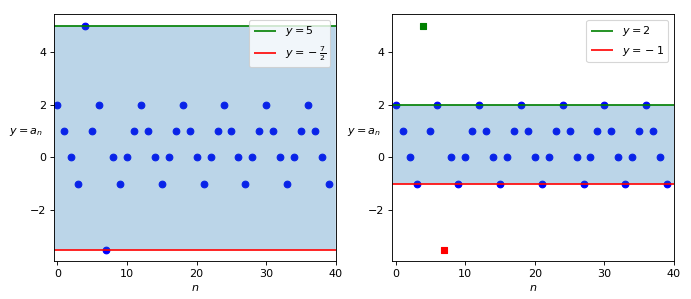
Using the statistical language, we can say that the terms a_4 and a_7 are outliers, i.e. some values that clearly differ from the others, and that for this reason are negligible. In descriptive statistics, two possible analyses that can be made on a data set are just the identification of the outliers and of some intervals that contain most data, a bit like we have done till now with our sequence. But the comparison with statistics ends here, because there is a big difference between the study of a statistical sample and the study of a sequence: the latter is an infinite sequence of data, whereas a statistical sample is finite. This changes many things. For example we could ask ourselves:
- If the value 5 was repeated infinite times, but only every 1000 terms of the sequence, would it still be negligible?
- Does it make sense to ask what is an interval containing more than tha 99% of the sequence terms?
The answers to both questions are negative:
- If the value 5 was repeated every 1000 terms, though it may be considered “rare”, it still would repeat itself infinite times! One thing is to neglect a single abnormal value, another thing is to neglect infinite ones.
- The 99%, or any fixed percentage greater than 0, of an infinite amount is still an infinite amount. There is no numeric difference between the 99%, the 50% or the 100% of infinite: they are all infinite in the same way.
So let’s try to understand what makes sense to ask ourselves when we study a sequence, containing infinite terms. An important concept, on which we’ll focus hereinafter, is the distinction between “all” and “almost all”. We’ll apply it to the terms of the sequence, but it’s more generally defined on any set of infinite elements:
- “All” means… just all the set! No element excluded.
- “Almost all” means all the set, except a finite number of elements.
Applying this concept to the set of the terms of a sequence, we can say that it’s meaningful to ask:
- What is an interval that contains all the terms of a sequence?
- What is an interval that contains almost all the terms of a sequence?
As we saw, in the case of the sequence shown in Figure 1, an interval that contains all its terms is [-\frac{7}{2}, 5], whereas one that contains almost all of them is [-1, 2]; in fact the latter interval contains all the terms except two, that is a finite number. These intervals are particular, because they are also the smallest possible ones, each for the respective category. In fact:
- Also [-4, 6], [-5, 10], [-10, 10], … are intervals that contain all the terms of the sequence, but they aren’t the smallest intervals with this property. The smallest is [-\frac{7}{2}, 5] because, if we made it smaller on the right, it would not include the term a_4 = 5; if we made it smaller on the left, it would not include the term a_7 = -\frac{7}{2}.
- Also [-2, 5], [4, 4] and [-3, 4] are intervals that contain almost all the terms of the sequence, but they aren’t the smallest intervals with this property. The smallest is [-1, 2] because, if we made it smaller on the right, it would not include all the sequence terms equal to 2, that are infinite; similarly, if we made it smaller on the left, it would not include all the terms equal to -1, that are also infinite.
We already used several times the word “infinite”, and we’ll continue often to use it in this post. It’s important to point out that we always refer to an infinity of countable kind, that is the same kind of infinity of the natural numbers. There are other kinds of infinity that are said to be uncountable, but we’ll not consider them in this post.
Infimum, supremum, limit inferior and limit superior of a real sequence
Now we could ask ourselves: does the smallest interval containing all, or almost all, the terms of a sequence always exist for all sequences?
The answer is anything but trivial. For the first question it’s affirmative, considering closed intervals:
Existence of the smallest closed interval that contains all the terms of a sequence
For every real sequence (a_n), there exists one and only one closed interval such that:
- It contains all the terms of the sequence
- It’s the smallest closed interval with the previous property
What does “smallest interval” exactly mean?
When in mathematics one person speaks about an object that is smaller, or greater, than another one, he or she always should clarify in what sense. When the objects are integer or real numbers, the question is rather trivial, but if we have two intervals I and J, how can we establish which one is the smallest? There are at least two ways:
- The smallest interval is the one with the smallest width (where the width is given by the difference between the two endpoints)
- The smallest interval is the one that is contained in the other one
Both these ways to interpret the concept of smallest interval have their own problems:
- In the first way, unlimited intervals cannot be adequately compared. For example the intervals [-1, +\infty], [-\infty, 1000] e [-\infty, +\infty] have all the same width (infinite), but they are very different from each other.
- In the second way, some unlimited intervals can be easily compared (for example [-1, +\infty] is greater than [3, +\infty], because it contains it). On the other hand, many couples of intervals are not comparable, in the sense that we cannot establish which is the smallest (for example the intervals [0, 2] and [1, 3] are not comparable, because neither of the two contains the other one).
In this post we’ll adopt the second definition, the one based on containment. This definition is also the most general, because it can be applied to any set, not only to intervals. The adoption of one definition rather that the other one, however, has relative importance in this post, because all that we’ll say, with small formal modifications, would still be valid if intervals were compared to themselves by width.
The following property, of which we’ll omit the proof, lets us define the infimum (\inf) and the supremum (\sup) of a real sequence, that are simply the endpoints of the interval given by Property A.1:
\inf and \sup of a real sequence
Given a real sequence (a_n), let I = [i, s] be the smallest closed interval that contains all the sequence terms. Then we define the following:
For example, in our case:
We can note that in Definition A.5 it’s not specified if the \inf and the \sup are two terms of the sequence. In the sequence a_n of Figure 5 it’s so, but generally the \inf and the \sup may be only some limit values that indeed do not correspond to any particular term. For example, the \inf of the sequence 1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \ldots is 0, but no term of the sequence is equal to zero.
In the case of unbounded sequences, the \inf or the \sup can be infinite. In this case the interval I of Definition A.5 can be of the kind [-\infty, s], [i, +\infty] or [-\infty, +\infty]. For example, the Fibonacci sequence 1, 2, 3, 5, \ldots (in which each term is the sum of the two previous ones) has 1 as \inf and +\infty as \sup. Note that the intervals of the kind [-\infty, s], [i, +\infty] or [-\infty, +\infty] are closed, as required by Definition A.5. In fact +\infty and/or -\infty, as appropriate, belong to such intervals, as if they were real numbers. The intervals [-\infty, s], [i, +\infty] and [-\infty, +\infty] so are not intervals in \mathbb{R}, but in the set \mathbb{R} \cup \{-\infty, +\infty\}.
Definition A.5 defines simultaneously the \inf and the \sup of a sequence, but there is also a way to define them separately. Let’s see this alternative definition, which is the canonical one:
\inf and \sup of a real sequence, canonical definition
Given a real sequence (a_n), we define the following:
The two definitions are equivalent, meaning that, if Definition A.5 is adopted as definition of the \inf and the \sup, then Definition A.6 can be proved as a property; conversely, if Definition A.6 is adopted, then Definition A.5 can be proved as a property. In this post we chose Definition A.5 because we consider it simpler and more intuitive.
On the basis of the previous example, we could be tempted to say that a property similar to A.1 is valid for the intervals that contain almost all the terms of the sequence, i.e. that there is always one of them which is the smallest. We’ll see that this is not true, taking as an example the sequence shown in Figure 3.
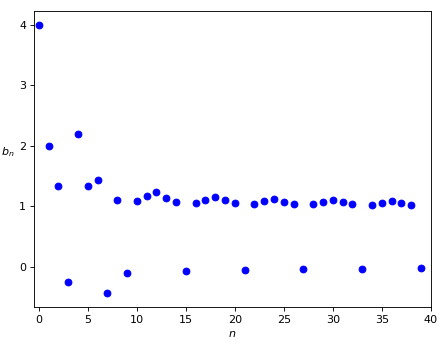
This sequence, that we’ll call (b_n)_{n \geq 0}, is defined starting from (a_n), as follows:
As it’s clear from the picture, the positive terms of the sequence tend to 1, whereas the negative ones tend to zero. The sequence on the whole does not have a limit, but it can be divided into two subsequences having different limits. But this is not the true difference with the previous sequence a_n, because also in a_n some subsequences with a limit can be found: for example the terms a_0, a_6, a_{12}, a_{18}, \ldots, a_{6k}, \ldots are all equal to 2, so all the more true they have limit 2.
The most important difference between the sequences (a_n) and (b_n) is that in the first one there exists the smallest interval containing almost all the terms of the sequence, in the second one it does not exist. Let’s see why. First of all in the sequence (b_n) no term is equal to 1 or to 0, even if the positive terms tend to 1 and the negative ones tend to 0: this is clear from the graph.
Why is no term of the sequence b_n equal to 1 or 0?
The reason is very simple. Any term of the sequence b_n is given by the formula \frac{a_n + 1}{n + 1} + 1 or by the formula \frac{a_n}{n}. Let’s suppose that b_n = 0. If b_n was obtained by the formula \frac{a_n}{n} = 0, a_n should be 0, but no term of the sequence (a_n) is 0; if instead it was obtained by the formula \frac{a_n + 1}{n + 1} + 1 = 0, a_n should be -n - 2, but it cannot be because, according to (1), the formula b_n = \frac{a_n + 1}{n + 1} + 1 = 0 is valid only when a_n \gt 0. We can reason in the same way for proving also that no term of the sequence is equal to 1.
The values 0 and 1 are so theoretical limits that are never actually reached: all the terms of the sequence are either smaller than 0, or greater than 1. It follows that the interval [0, 1] does not contain any term. Then, if we want to find the smallest interval that contains almost all the terms of the sequence, we have to extend the interval [0, 1] both on the right and on the left, in order to include both the terms greater than 1 and those ones smaller than zero (both infinite).
Actually, it can be proved that any interval greater than [0, 1] contains almost all the terms of the sequence, and that there is no one which is smaller than all the others.
Why does any interval greater than [0, 1] contain almost all the terms of the sequence, and there is no one that is smaller than all the others?
Let’s suppose for simplicity to extend the width of the interval of the same amount both on the right and on the left; for example, if the amount is \frac{1}{5} we’ll obtain the interval I := [0 -\frac{1}{5}, 1 + \frac{1}{5}] = [-\frac{1}{5}, \frac{6}{5}]. How many terms of the sequence does this interval contain?
Let’s start from the negative terms. Since they tend to zero, becoming smaller and smaller in absolute value, from a certain point of the sequence on (that is “definitively”, using the terminology of asymptotic analysis) they will always be greater or equal to -\frac{1}{5}. So there exists a certain constant k such that, for every n \geq k, all the negative terms b_n are greater or equal to -\frac{1}{5}. Therefore the only sequence terms that can be negative and not belong to the interval I are b_0, b_1, b_2, \ldots, b_{k-1}: they are at most k terms (actually they are less than k, because the listed terms include also the positive ones; but in the worst hypothesis, that is if no positive term exists, they would be k).
About the positive terms we can argument in a similar way. Since they tend to 1, becoming smaller and smaller, they will be definitively smaller or equal to \frac{6}{5}. So there exists a certain constant h such that, for every n \geq h, all the positive terms b_n are less than or equal to \frac{6}{5}. So the only sequence terms that can be positive and not belong to the interval I are b_0, b_1, b_2, \ldots, b_{h-1}: they are at most h terms.
Summarizing, at most k + h sequence terms, that is a finite number of terms, can be outside of the interval I = [-\frac{1}{5}, \frac{6}{5}]. So this interval contains almost all the terms of the sequence (see Figure 4).
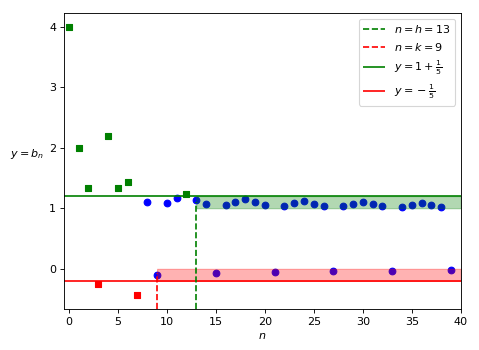
But then, if the interval [0, 1] does not contain any term b_n, and the interval [-\frac{1}{5}, \frac{6}{5}] contains almost all of them, certainly the smallest interval that contains almost all the terms must be intermediate between the two. However, no matter how long we can try to look for this interval, we’ll never find it… bacause it does not exist! In fact, like for constructing the interval I we started from the interval [0, 1] widening it by \frac{1}{5} both on the right and on the left, if instead of \frac{1}{5} we took another positive constant \epsilon, obtaining the interval I_{\epsilon} := [-\epsilon, 1 + \epsilon], nothing would change, because also this interval would contain almost all the terms, for any \epsilon. In fact, even supposing the constant \epsilon to be very small, there will always exist some indexes k_{\epsilon} and h_{\epsilon} such that all the negative sequence terms with index greater or equal to k_{\epsilon} are greater or equal to -\epsilon, an all the positive terms with index greater or equal than h_{\epsilon} are less than or equal to 1 + \epsilon. The smaller \epsilon is, the bigger k_{\epsilon} and h_{\epsilon} will be, but they will still be finite. So the interval I_{\epsilon} does not include at most k_{\epsilon} + h_{\epsilon} sequence terms, that is a finite number, so it contains almost all of them.
From that we can deduce that there is not one smallest interval that contains almost all the sequence terms. This comes from the fact that there is no real positive number that is the smallest (in contrast to integer numbers). In fact, we saw that any constant \epsilon \gt 0 corresponds to an interval I_{\epsilon} = [-\epsilon, 1 + \epsilon] which contains almost all the sequence terms; making \epsilon smaller, this interval becomes smaller and smaller, but there not exists a smallest interval, because there not exists a smallest positive \epsilon.
Summarizing, we saw that the interval [0, 1], though not containing any term of the sequence (b_n), has a particular property: any interval properly containing it, contains almost all the sequence terms. In other words, we pass from zero to almost all the terms with even a very small enlargement of the interval, no middle ground. But another interesting thing is that the interval [0, 1] is the smallest interval with this property. In fact, we can prove that the property is valid also for all the intervals greater than [0, 1], while it is not for all the smaller ones:
- We said that, if A is an interval greater than [0, 1], it contains almost all the sequence terms. So the property holds for A because, as A itself contains almost all the terms, this will be all the more true also for any interval greater than A.
- If B in an interval smaller than [0, 1], the property does not hold for B, because it’s not true that all the intervals greater than B contains almost all the sequence terms; in fact [0, 1] in greater than B but does not contain any term.
So [0, 1] is not the smallest interval that contains almost all the sequence terms (that does not exist), but the smallest interval such that any interval greater than it contains almost all the sequence terms. It can be proved (but we don’t do it) that such an interval exists for any real sequence:
Existence of the smallest interval such that any interval greater than it contains almost all the terms of a real sequence
For any real sequence (a_n), there exists an interval such that:
- Any interval greater than it contains almost all the terms of the sequence
- It’s the smallest interval with the previous property
We can note that the interval that satisfies Property A.2 does not necessarily contain almost all the sequence terms: the intervals greater than it do. This is just what happens in our example: the interval [0, 1] does not contain almost all the sequence terms, actually it does not contain any one!
As well as Property A.1 lets us define \inf and \sup of a sequence, Property A.2 lets us define \lim \inf and \lim \sup, that are the endpoints of the interval that satisfies it:
\lim \inf and \lim \sup of a real sequence
Given a real sequence (a_n), let I = [i, s] be the interval that satisfies Property A.2. Then we define the following:
In the case of the sequence b_n, as we saw:
Alternative definition of \lim \inf and \lim \sup
Like we pointed out before about \inf and \sup, similarly the canonical definition of the \lim \inf and the \lim \sup of a sequence is not Definition A.7, but the following that defines them separately:
\lim \inf and \lim \sup of a real sequence, canonical definition
Let (a_n) be a real sequence.
We define \lim \sup a_n as the real number s such that:
- If (a_n) is bounded above:
- Almost all the sequence terms are less than or equal to s
- It’s the smallest number with the previous property
- Otherwise, s = +\infty
We define \lim \inf a_n as the real number i such that:
- If (a_n) is bounded below:
- Almost all the sequence terms are greater or equal to i
- It’s the greatest number with the previous property
- Otherwise, i = -\infty
As well as Definitions A.5 and A.6, Definitions A.7 and A.8 are equivalent: having chosen one of the two, the other can be proved as a property.
Relationship between the limit superior, the limit inferior and the limit of a sequence
We conclude by stating two important properties that link the \lim \inf and the \lim \sup of a sequence, on one side, and its limit, on the other side.
We saw that, in the sequence (b_n) shown in Figure 3, the \lim \inf and the \lim \sup are different, and the sequence doesn’t have a limit, but it oscillates continuously between the \lim \inf (0) and the \lim \sup (1), approximating now to one and now to the other. This fact is not a characteristic of our example, but it’s true in general. In fact the following Proposition can be proved:
Any real sequence with \lim \inf different from \lim \sup does not have a limit
Any real sequence (a_n) such that \lim \inf a_n \neq \lim \sup a_n does not have a limit.
Let’s see instead what happens when \lim \inf and \lim \sup are equal.
Let’s consider the sequence (c_n) defines as follows:
By drawing the graph we can see clearly that this sequence tends to zero:
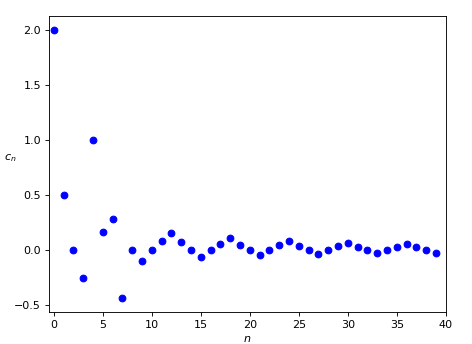
Let’s ask ourselves now: according to Definition A.7, what are the \lim \inf and the \lim \sup of this sequence? We’ll start, like before, from the analysis of the intervals that contain almost all the sequence terms. Intuitively, since the sequence terms tend to concentrate around the zero, both above and below it, an interval that contains almost all the terms necessarily must contain the zero.
Indeed, like before, it can be proved that any interval that contains zero in its interior, contains almost all the terms of the sequence.
We can consider by simplicity an interval with the same width both on the right and on the left of the zero, that is of the kind [-\epsilon, \epsilon], for some constant \epsilon \gt 0. Indeed, it can be proved (using the definition of limit) that such an interval contains, for any \epsilon, almost all the terms of the sequence, in particular all the terms with an index greater or equal to a certain constant k_{\epsilon} \gt 0 (see Figure 6).
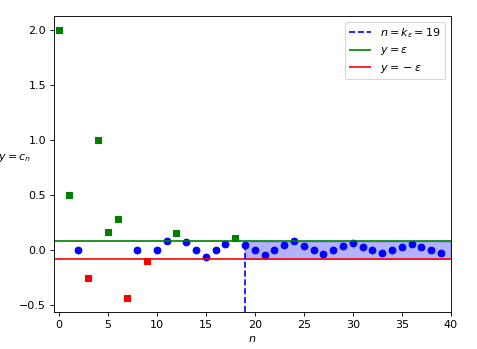
So we get back to the same argument as before: by making \epsilon smaller we can find infinite intervals of the kind [-\epsilon, \epsilon], all of which contain almost all the terms of the sequence.
But we want to find a closed interval which satisfies Definition A.7. So this interval must be smaller than all the intervals that contain 0 in their interior… Then there is only one possibility, and it’s a very particular interval: it’s the interval [0, 0], having 0 as both the endpoints, so not as an interior point. It’s indeed the set reduced to just the number 0, but it’s still a closed interval, and it satisfies Definition A.7.
The interval [0, 0] satisfies Definition A.7 because it satisfies both points of it:
- All the intervals of the kind [-\epsilon, \epsilon], that are greater than [0,0], contain almost all the sequence terms (the same thing is true for any greater interval, also with endpoints different in absolute value, but for simplicity we don’t consider this more general case).
- About the fact that it’s the smallest interval with the previous property, the problem does not arise, as it is reduced to a single point, so there is no smaller interval (the empty set is not an interval).
So, according to Definition A.7:
We can note a strong analogy between this sequence and the previous one: for example, as well as the interval [0,1] does not contain any term of the sequence (b_n), the interval [0,0] does not contain any term of (c_n).
But there is a substantial difference between the two sequences: the sequence (c_n) has a limit, and its \lim \inf coincides with its \lim \sup, instead the sequence (b_n) has the \lim \inf different from the \lim \sup and, by Proposition A.1, has not a limit. Also for the case of (c_n), the relationship we noted among the limit inferior, the limit superior and the limit is true generally for any real sequence:
Any real sequence with \lim \inf equal to \lim \sup has a limit
Any real sequence (a_n) such that \lim \inf a_n = \lim \sup a_n has a limit, and \lim a_n = \lim \inf a_n = \lim \sup a_n.
Joining Propositions A.1 and A.2, we can immediately obtain the following Property:
A real sequence has a limit if and only if its \lim \inf and its \lim \sup are equal.
A real sequence (a_n) has a limit if and only if \lim \inf a_n = \lim \sup a_n, and in this case \lim a_n = \lim \inf a_n = \lim \sup a_n.
In theory the previous Property may be used as the definition of the limit of a sequence: this way this limit would not be defined as a separate entity, but on the basis of the limit inferior and the limit superior.
In the next post we’ll apply this Property to the function \frac{\pi(x)}{x}.