Prerequirements:
The properties of the divisors of natural numbers which we saw in the previous post let us define a function which is very important in number theory, the Möbius function, indicated by the symbol \mu. It’s often used in summations in which the variable does not vary between a minimum and a maximum, but it assumes as possible values all and only the positive divisors of a natural number.
Generalization of the two properties of the divisors and definition of the Möbius function
Let’s go back to Property N.9 (A property about the product of divisors of a positive integer number with at least two distinct prime factors), according to which, if n is a positive integer number with at least two distinct prime factors, taken its square-free divisors, the product of those ones which are the product of an even number of prime factors is equal to the product of those ones which are the product of an odd number of prime factors. For example, if n = 60:
where on the right there are the square-free divisors of 60 which are the product of an odd number of prime factors (for example 30 = 2 \cdot 3 \cdot 5), and on the left there are its square-free divisors which are the product of an even number of prime factors (among which 1, product of zero prime factors).
Equation (1) can be rewritten as follows:
In this formulation it’s clear that the divisors which are the product of an even number of prime factors are raised to the exponent 1, while the ones which are the product of an odd number of prime factors are raised to -1. We can write this equality in a compact way by introducing a function that, given a square-free divisor d of 60, returns the appropriate exponent. We’ll call such a function \mu. We can define it by using the notations E_n e O_n introduced with Property N.8:
for all d \in \{\text{square-free divisors of } 60.
Using this notation, (2) can be rewritten as follows:
This formula can be made even simpler by considering also the divisors of 60 which are not square-free. We can include these divisors in (2) by raising them to a zero exponent, thus not changing the final product:
Not it’s useful to extend the previous definition of \mu, including also the divisors which are not square-free. For this purpose, let’s introduce the following notations, which resume and extend the ones of Property N.8, and which will let us lighten the following formulas:
Sets of divisors of a positive integer number
Let n \in \mathbb{N}^{\star}. The following sets are defined:
- E_n := \left\{ \text{square-free divisors of $n$ which are the product of an even number of prime factors} \right\}
- O_n := \left\{ \text{square-free divisors of $n$ which are the product of an odd number of prime factors} \right\}
- Q_n := \left\{ \text{divisors of $n$ which are not square-free} \right\}
We can note that every divisor of n belongs to one and only one of the sets E_n, O_n and Q_n. In other words, the set \{E_n, O_n, Q_n\} is a partition of the set of the divisors of n.
Using Definition N.17, the function \mu can be defined in a more general way, as follows:
for all d \in \{\text{divisors of $60$}\}.
The advantage of this definition is that, starting from (2′), we can obtain a simple production extended to all the divisors of 60:
This procedure can be generalized to any positive integer n satisfying Property N.9, i.e. having at least two distinct prime factors, as follows:
where the function \mu is defined like in (3′), putting n in place of 60; hence
for all d \in \{\text{divisors of $n$}\}.
How can formula (5) be simplified if n is square-free?
If n is square-free, also all its divisors are square-free, hence
and
while
so (5) becomes:
We can note that the definition of \mu given by (3”) does not depend on n, but only on d. In fact, whether a divisor d is square-free, or it’s a product of an even or an odd number of prime factors, it depends only on d itself, not on the number which it’s a divisor of. So we can define \mu for any positive integer, which however we’ll continue to call d for remembering that usually it’s a divisor of some other previously fixed number, even if it’s irrelevant for the purpose of the definition:
Möbius function
We define the function \mu: \mathbb{N}^{\star} \rightarrow \{-1, 1, 0\} such that:
for all d \in \mathbb{N}^{\star}. The function \mu is called Möbius function.
Formula (5) can be regarded as an alternative form of Property N.9:
A property about the product of divisors of a positive integer number with at least two distinct prime factors
Let n be a positive integer number with at least two distinct prime factors. Then:
The Möbius function can be used for writing differently also Property N.8 (A property about the count of divisors of an integer number greater than 1). This Property states that, for every integer n \gt 1:
In order to compute the cardinality of a finite set, it’s enough to associate the number 1 to each element of the set, and summing up everything:
Hence, by (6):
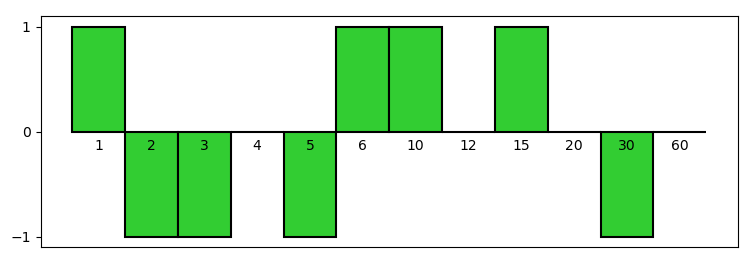
So, Property N.8 states that, if we count 1 for each element of E_n and -1 for each element of O_n, and we sum up everything, the final result is zero.
In this calculation we may consider also the possible divisors of n which are not square-free (thus belonging neither to E_n nor to O_n, but to Q_n): it’s sufficient to count them as 0, in order not to alter the sum:
Now it’s clear that this equation can be expressed in a compact form by using the definition of \mu(d), that is 1 if d \in E_n, -1 if d \in O_n, and 0 if d \in Q_n:
Thus we have obtained the following alternative form of Property N.8:
A property about the count of divisors of an integer number greater than 1
Let n \gt 1 an integer number. Then:
Figure 1 shows this Property for n = 60. The values of the Möbius function are depicted as rectangles, like in Figure 1 of the post From integer numbers to real numbers – second part.
Connection between the Möbius function and the function \Lambda
The advantages of the Möbius function are not limited to the possibility of writing in a more concise way some formulas. The main advantage is that it’s very suitable to be employed into algebraic expressions which involve summations od productions extended to all the divisors of a given natural number, like (7). As we’ll see later, in this post and in the following ones, summations of this kind are very common in number theory. However, before continuing, we have to overcome some little limitations of Property N.9 (second form) and N.8 (second form). The first one, in fact, is applicable only to positive integer numbers with at least two distinct prime factors, and the second one is applicable only to numbers greater than 1. In order to study adequately the properties of the divisors of natural numbers, we need some properties that are valid for all positive integer numbers; we can disregard only 0, because it’s the only natural number that, according to Definition N.2 (Divisibility) has no divisors. So, Property N.9 (second form) lacks positive integer numbers that have only one distinct prime factor (that are the powers with a positive exponent of a prime number) and the number 1, which has no prime factors, while Property N.8 (second form) lacks only the number 1. Now let’s try to fill these gaps.
Let’s start from Property N.9 (second form). First of all, if n = 1, we’ll have:
where we used the fact that \mu(1) = 1, because 1 is square-free, since it’s not divisible by any square greater than 1, and is the product of an even number (zero) of prime factors.
If instead n = p^a, with a \in \mathbb{N}^{\star}, we have to note that the divisors of n are 1, p, p^2, \ldots, p^a, and that among them only 1 and p are square-free, and they are respectively the product of an even number and of an odd number of prime factors. So:
Summarizing, we can say that:
- if n is the power of a prime number p with a positive exponent, then \prod_{d \mid n} d^{\mu(d)} = \frac{1}{p};
- in the other cases, i.e. when n = 1 or when n is the product of at least two distinct prime factors, \prod_{d \mid n} d^{\mu(d)} = 1.
Do you recognise something familiar? This function if the inverse of the function \Lambda^{\star}, which we introduced when talking about the factorial; in fact \Lambda^{\star} returns p in the first case and 1 in the second one. Thus we can generalize Property N.9 (second form) as follows:
A property about the product of divisors of a positive integer number
Let n \in \mathbb{N}^{\star}. Then:
The logarithmic version of this Property will be often useful:
A property about the product of divisors of a positive integer number
Let n \in \mathbb{N}^{\star}. Then:
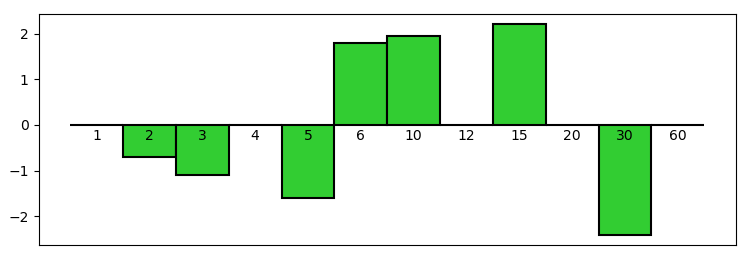
Applying the logarithm to both members of Property N.10, and using the definition of function \Lambda, we’ll have:
The latter Property is shown in Figure 2, in the case of n = 60.
Now let’s see how we can extend Property N.8 (second form), considering the number 1. If n = 1, we’ll have that:
So we can say that the function \sum_{d \mid n} \mu(d) is 1 if n = 1 and 0 otherwise:
A property about the count of divisors of a positive integer number
Let n \in \mathbb{N}^{\star}. Then:
We can get a first idea of how the Möbius function is versatile inside algebraic expressions, by simply substituting \frac{n}{d} in place of one d into Property N.10, as follows:
The result is rather surprising. If by Property N.10 the production \prod_{d \mid n} d^{\mu(d)} is equal to \frac{1}{\Lambda^{\star}(n)}, making the substitution above we’ll obtain exactly the inverse, that is \Lambda^{\star}(n):
Expression of \Lambda^{\star} by means of \mu
Let n \in \mathbb{N}^{\star}. Then:
In order to prove this Property, we’ll distinguish the same cases that brought us to the proof of Property N.10:
- n has at least two distinct prime factors
- n is the power of a prime number with a positive exponent
- n = 1
First of all we can rewrite the product \prod_{d \mid n} \left( \frac{n}{d} \right)^{\mu(d)} as follows:
Thus we find again, at the denominator, a product we already know, by Property N.10. So let’s see what the numerator is equal to. It’s another product, which we can break by distinguishing the three types of divisors of n: the ones belonging to E_n, the ones belonging to O_n, and the ones belonging to Q_n. Remembering that in these three cases the value of \mu(d) is respectively 1, -1 and 0, and remembering that |E_n| = |O_n| by Property N.8, we’ll have that:
Then, by substituting into (a) and applying Property N.10, we’ll obtain:
which completes the proof.
Like we did before for Property N.10, we can state the logarithmic form of Property N.12 too:
Expression of \Lambda by means of \mu
Let n \in \mathbb{N}^{\star}. Then: