
We’ll start our study of prime numbers explaining the definition of prime number. What’s commonly known is that a prime number is a positive integer number divisible only by itself and 1. This is true except for number 1, that according to that should be prime (1 is divisible by 1, which is also the number itself), but indeed it isn’t. Number 1 in fact is a priori excluded from prime numbers. The reason is related to a theorem, known as the Fundamental Theorem of Arithmetic:
Fundamental theorem of arithmetics
Every integer number greater than 1 can be written as a product of prime numbers. Moreover such expression, called factorization or decomposition into prime factors, is unique apart from the order of the factors.
| 150 | 2 |
| 75 | 3 |
| 25 | 5 |
| 5 | 5 |
| 1 |
The following passages are applied:
- Computation starts by 150, which is written at the top of the left column, and it’s divided by its smallest prime divisor, which is 2, obtaining 75; the divisor is written at the top of the right column;
- The result of the division is in turn written in the left column, and the process is repeated on it, by dividing time after time by the smallest possible prime divisor;
- When the result of the division is 1, the process ends;
- Finally, we have 150 = 2 \cdot 3 \cdot 5 \cdot 5. This result can also be written in a more compact way, by considering that the product of a number with itself, by definition, is a power: 150 = 2 \cdot 3 \cdot 5^2.
If the starting number is small and the prime factors to be found are few, the operation is very simple, but this is not always the case. As you can verify with the factorizer, for example, a relatively small number like 1024 needs many divisions, and numbers formed by big prime factors, like 89077, require many attempts in order to find a prime divisor. Moreover, if the prime factors are extremely big, finding them becomes a real challenge, as it turned out in the RSA Factoring Challenge, which consisted in starting from some numbers obtained by multiplying two very big primes which are known (but not revealed by the organizers), and trying to factorize the former: for some of them, by now, every attempt has failed.
If 1 was considered prime, the Fundamental theorem of arithmetics could not be true in its current form and it should be expressed differently, adding an exception. As a consequence, a myriad of theorems that, directly or not, depend from it should be modified in turn, introducing some often unconvenient exceptions… indeed the most simple solution is assuming that 1 is not prime.
The product mentioned in the statement of the Fundamental Theorem of Arithmetic can be made up of any number k of prime factors, not necessarily distinct. For example 12 = 2 \cdot 2 \cdot 3 is the product of k = 3 prime numbers. Usually a product is defined for at least k = 2 factors, however for the theory we are getting ready to develop, it will be convenient to extend the idea of product including the case of the product with just one factor (k = 1), which is the factor itself. With this assumption, a prime number il also a product of prime numbers: a special product, made up of the number itself that multiplies no other number. For example, here are the factorizations of numbers from 2 to 10:
| Number | Factorization | Number of factors |
|---|---|---|
| 2 | 2 | 1 |
| 3 | 3 | 1 |
| 4 | 2 \cdot 2 | 2 |
| 5 | 5 | 1 |
| 6 | 2 \cdot 3 | 2 |
| 7 | 7 | 1 |
| 8 | 2 \cdot 2 \cdot 2 | 3 |
| 9 | 3 \cdot 3 | 2 |
| 10 | 2 \cdot 5 | 2 |
The fundamental Theorem of arithmetic states not only that every integer number greater than 1 has a factorization into prime factors, but also that this factorization is unique except for the order of the factors. For example, 12 = 2 \cdot 2 \cdot 3 and there are no other prime numbers, apart from 2 taken two times and 3 taken one time, that multiplied between themselves make 12. The unicity of the factorization is a fundamental property that is at the base of many theorems of number theory, and it’s right here that we can understand why 1 is not considered a prime number. In fact, if 1 was prime, every positive integer would have infinite factorization into prime numbers. For example
In order to avoid this, and to be certain to always have a unique factorization, 1 is not considered prime. For this reason the fundamental theorem of arithmetic holds for integers greater than 1: it cannot hold for 1, because it’s not prime and is only the product of itself, so it’s not a product of primes.
Having excluded the number 1 from prime numbers, we can state a correct definition of prime number:
Prime number
A prime number is an integer number greater than 1, which is divisible obly by itself and 1.
This definition refers to the concept of divisibility, which is worth to point out:
Divisibility
An integer a is divisible by an integer b, with b \neq 0, if a = b c for some integer c.
If a is divisible by b we write b \mid a (“b divides a“), otherwise we write b \nmid a (“b does not divide a“).
For example, 10 is divisible by 2 because it can be written as 10 = 2 \cdot 5, where 5 is an integer c such that 10 = 2 \cdot c. On the contrary, 10 is not divisible by 3 because there isn’t any integer c such that 10 = 3 \cdot c. In other terms, we can say that 2 divides 10 (2 \mid 10) and 3 doesn’t divide 10 (3 \nmid 10).
Definition N.2 doesn’t contemplate the case of b = 0, so it remains undefined whether a number is divisible by 0 or not.
Here the exclusion of a particular case from a general definition is for a good reason as before, for the purpose of preserving some fundamental and convenient properties, which aren’t valid for the excluded case. In fact we can observe that the number c is univocally determined when a and b have been fixed (with the fraction notation we can write c = \frac{a}{b}), which is not true if a = b = 0. In this case in fact we have 0 = 0 c for any integer c and not for a specific one. Indeed, for the purpose of guaranteeing the unicity of c, it would be enough to exclude from the definition just the case of a and b both 0, instead of b = 0: this point could be examined further, but certainly is a matter of secondary importance.
An immediate consequence of the definition of divisibility is the following:
Within natural numbers, a divisor is less than or equal to a positive dividend
Let a and b be two natural numbers, with a \gt 0. If b \mid a, then b \leq a.
If b \mid a, then by Definition N.2 there exists an integer c such that bc = a. By the sign product rule, this integer cannot be negative, because by hypothesis a and b are natural numbers, hence positive. In addition, c cannot be zero, because, if so, then a = bc = b \cdot 0 = 0, but by hypothesis it must be a \gt 0. So c \geq 1. Then b = b \cdot 1 \leq bc = a, hence b \leq a.
Divisibility has a lot to do with the factorization into prime numbers: in fact, if b \mid a – that is a = b c for some integer c – it means that somehow b is present in the factorization of a, as a prime or as a product of primes. For example:
- 2 \mid 10 and 2 is present in the factorization of 10 as a prime number: 10 = \mathbf{2} \cdot 5;
- 6 \mid 24 and 6 is present in the factorization of 24 as a product of primes: 24 = 2 \cdot 2 \cdot \mathbf{2 \cdot 3};
- Also 8 \mid 24 and 8 is present in the factorization of 24 as a product of primes: 24 = \mathbf{2 \cdot 2 \cdot 2} \cdot 3;
So if b \mid a it means that the factorization of b is contained into the factorization of a. In particular, if a prime number p \mid a, p must be one of the primes of the factorization of a. For example, if a = p_1 p_2, with p_1 and p_2 primes, it must be p = p_1 or p = p_2. This simple property characterizes prime numbers so strongly that, if conveniently generalized, it can be taken as an alternative definition of prime number:
Prime number, characteristic property or alternative definition
A prime number is an integer number p > 1 such that, if p \mid bc, then p \mid b or p \mid c, for any integers b and c. In other terms, p cannot divide a product of integers bc without dividing at least one of the two factors.
Clearly, if we had chosen the previous statement as the definition of prime number, then Definition N.1 would have become a property to be proved on the basis of Property N.1B. Instead, since we chose Definition N.1 as the definition of prime number, then the latter is the starting point for proving Property N.1B. We’ll not see this proof, but let’s try to understand the statement. Let’s decompose the number bc into prime factors: for example if b = 6 and c = 10, bc = 60 and
But since 60 is the product of 6 and 10, we can reorder its factorization in such a way to find the prime factors of 6 and those of 10:
For the reasoning above, if p is a prime number dividing 60, p must be present in its factorization (that is p = 2 or p = 3 or p = 5); but then, for how we subdivided it, p can be present in the factorization of 6 (that is p = 2 or p = 3), and in that case it would divide 6, or it can be present in the factorization of 10 (that is p = 2 or p = 5), and in that case it would divide 10. Possibly p can be present in both factorizations, as the case of p = 2, but it must be present at least in one of them. To better understand this, we can imagine to apply the following algorithm: we scan the list of the prime factors of 60 in the ordering of (1): 2, 3, 2, 5; if we find p in the first two positions, we say that p \mid 6; otherwise we say that p \mid 10. In this way, if p isn’t a divisor of 60 we won’t find it and we won’t say anything; if instead p \mid 60 we will find it in one or more positions and we’ll say at least one utterance between “p \mid 6” and “p \mid 10“.
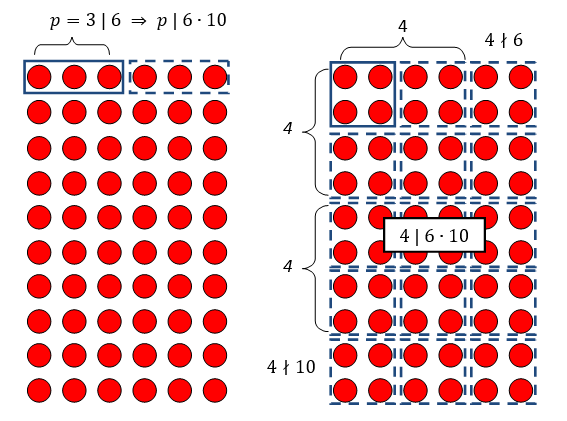
It’s also interesting to observe what happens in the case of a not prime number (which is called a composite number), like 4. We have that 4 \mid 60, so the factorization of 4 must be contained in that of 60. But 4 isn’t prime, so 4 cannot be present in the factorization of 60 as a prime number, but it must be present in the form of a product of prime numbers. This is the reason why 4 divides 60 without dividing 6 and 10, how you can see highlighting the prime factors of 4 (2 \cdot 2) in (1):
We can see that the number 4 “breaks” into a 2 appearing among the divisors of 6, and another 2 among the divisors of 10: therefore 4 does not divide either 6 or 10, but it divides their product 60. this cannot happen with a prime number, because a prime number cannot “break” between the factors b and c: it must appear “intact” inside one of them.
Tha last example is represented graphically in the picture below:
Infinity of prime numbers
An important theorem, well known since ancient times, which is a consequence of the definitions above and the Fundamental Theorem of Arithmetic, is the following:
Infinity of prime numbers
The number of primes is infinite.
The proof is so famous and simple that it’s worth to remember it. Let’s suppose that only a finite number N of prime numbers exists. In this case, we could list all the prime numbers in increasing order: p_1, p_2, \ldots, p_N, where p_N is the biggest prime number. So, starting from this list of prime numbers, we can construct the number
For how it’s defined, this number is not divisible by any of the primes p_1, p_2, ..., p_N.
Let’s ask ourselves the question: which prime numbers M is divisible by? Let’s see if for example it’s divisible by p_1. If it was, by Definition N.2 (Divisibility) an integer c would exist, such that
Hence, gathering p_1:
So, again by Definition N.2, p_1 \mid 1. Then, by Property N.1A, it should be p_1 \leq 1; but this is not possible because prime numbers, by Definition N.1, must be greater than 1. This means that the hypothetical number c of equation (4) cannot exist, i.e. M is not divisible by p_1.
The argument above does not depend on the choice of p_1, in fact it may be repeated also for all the other primes p_2, \ldots, p_N, with the result that M is not divisible by any of the primes p_1, p_2, \ldots, p_N.
By the Fundamental Theorem of Arithmetic, M is factorizable as a product of prime numbers. By Definition N.2, all the prime numbers which appear in the factorization of M divide it; so, for what we have seen before, they cannot be equal to either of the primes p_1, p_2, ..., p_N. But this is absurd, because we supposed that p_1, p_2, ..., p_N are the only existing prime numbers. This means that the initial hypothesis, that only a finite number of prime numbers exists, is wrong: there are infinitely many prime numbers
Hi, I have been enjoying reading through your website, as one of the most accessible websites to explain number theory. But I think there is an error in your explanation of the infinity of primes. You ask the question:
Why must M be prime, by the Foundamental Theorem of Arithmetic?
M is not necessarily prime, and an example that shows this is 2.3.5.7.11.13+1=30031 which is not a prime (its prime factors are 59 and 509). So the infinity of primes proof should say that either M is a new prime number OR there exist new prime numbers greater than p_N that enable M to be factorised, because p_1…p_N cannot be factors. For the first few cases eg 2.3+1=7, 2.3.5+1=31 etc M is indeed prime, but you don’t have to look very long to find the example quoted above.
Hi Tim,
we are happy to know that you are enjoying our website!
Thanks for your question. You are right: indeed there was an error in the proof of the infinity of prime numbers. We corrected the proof and we also simplified it.
We appreciated your help for improving our website. If you note any other errors, please don’t hesitate to contact us again.