Prerequisites:
If you sufficiently linger over the sequence of prime numbers up to a certain x (for example https://primes.utm.edu/lists/small/1000.txt, you will note that it’s difficult to find regularities. However this sequence has many interesting properties, some of which are also evident from a purely empirical analysis, but difficult to prove. What we’ll do henceforth is to examine in depth the sequence, reconstructing the chain of arguments that brings to the famous Prime number theorem, avoiding to lose the contact with numbers as much as possible, although along the way we will introduce several “superior” concepts.
A way to start investigating the sequence of prime numbers is to consider, starting from the beginning, portions of increasing size. For example, you can begin start with the study of the prime numbers up to 10 (2, 3, 5, 7), then up to 20, 30, etcetera, increasing the size of the considered portion by a fixed amount each time. Or you can start with the study of the prime numbers up to 10, then up to 20, the up to 40, etcetera, doubling each time the size of the considered portion. The latter approach will reveal itself to be effective, as it is based on product. In fact, since prime numbers are defined starting from the concepts of divisibility (Definition N.1) and product (Definition N.2), it’s not surprising that, while studying these numbers, the most used operation is the product indeed. In particular, we can fix a number x and consider the product of all prime numbers up to x. We will call this quantity, function of x, \theta^{\star}(x):
Product of prime numbers up to x
The following function is defined:
Where x is a positive integer number.
Let it be known, henceforth, that the variable p indicates a prime number. The trivial cases are:
- \theta^{\star}(1) = 1, because there are no primes up to 1 and assume that the product of an empty set of terms is 1 (in the post The definition of prime number we already assumed that the product of a single number is the number itself);
- \theta^{\star}(2) = 2, because 2 is the only prime number up to 2.
A non-trivial case is for example x = 20:
It’s a big number for manual calculation, but we are not interested in writing it explicitly.
We can note that \theta^{\star}(19) = \theta^{\star}(20), bacause 20 is not prime. However it’s convenient to start with 20 that’s even, because in this way we can split the set \{1, \dots, 20\} into equal parts, and so we can compare the product of primes up to 20 with that of primes up to 10:
We have 4 primes between 1 and 10 and just as many between 10 and 20: it’s a coincidence, in fact it’s almost never true that between a generic integer y and 2y there are as many primes as between 1 and y, especially as y increases.
If we multiply \theta^{\star}(20) by the non-prime numbers up to 20, we obtain the product of all numbers up to 20, that is 20! (the so-called “factorial” of 20). Let’s write this product highlighting prime numbers:
We can do the same with x = 10:
Of course the product of the first 10 numbers, that we have in (2), appears in (1) too, so we can divide member by member and obtain:
Now we have the product of numbers between 11 and 20, both primes and not: it would be a really good thing to isolate among them the prime numbers, highlighted above. Making mathematically this operation would require a knowledge of the sequence of prime we don’t have, but with a little trick we can do something similar.
We can note that the expression \frac{20!}{10!} greatly resembles the binomial coefficient
In practice for obtaining the binomial coefficient \binom{20}{10} starting from \frac{20!}{10!} it’s enough to divide again by 10!, so starting from (3) we have:
Now let’s go back to prime numbers: we wanted to separate as much as possible prime numbers from the non-primes, in (3). Well, dividing by 10! we did right that: in fact none of the prime numbers highlighted at the numerator of (4) divides 10!, because they are all greater than 10, so in the division by 10! cannot be cancelled. Essentially we found a divisor of the product (3) containing all primes between 11 and 20. Let’s do the division explicitly in order to show that, indeed, we are cancelling only non-prime factors:
We have obtained the product of primes we were looking for, up to a factor 4: not bad, for a so simple technique.
Putting it into (4) we have:
In particular, we certainly have that:
In this relation there is the essence of what we are looking for: an estimation (in this case an overestimation) of a product of consecutive primes, contained into an interval of integer numbers. However, the argument has still to be refined, because:
- Up now we tacitly assumed that x is even: in fact, starting from x = 20 we split the set \{1, \dots, x\} into two exactly equipotent parts (that is, parts with the same number of elements), but this is possible only if x is even. We have to see what happens if x is odd.
- We need an estimation of the product of all prime numbers up to x, not only those from a certain point onwards.It’s necessary to iterate the procedure for obtaining an estimation including the missing primes too.
- Binomial coefficients are not easily manageable in calculation: we can majorize them too, replacing them with a more simple expression. For this purpose the estimates seen in the post Binomial estimates can be employed.
Concerning the case of odd x, it’s enough to see what’s different between the previous development, with x = 20, and the development we would have with x = 21. In this case we cannot split the set \{1, \dots, 21\} into two equipotent subsets, but we have to choose between the partitions \{\{1, \dots, 10\}, \{11, \dots, 21\}\} and \{\{1, \dots, 11\}, \{12, \dots, 21\}\}.
In the first case, passage (3) would become:
Now for obtaining a binomial, as in passage (4), we should proceed as follows:
But this passage is not in the logic of what was developed before, because the prime numbers at the denominator are not completely preserved, but the 11 is cancelled.
So let’s see if things work differently in the second case. Passage (3) would be:
From which, passing to the most similar binomial to the left side, we have \binom{21}{11} again:
Now no prime number is cancelled between the numerator and the denominator, but we lost 11 anyway. So we can say that in both cases we are talking about the product of prime numbers between 12 and 21, where 12 is half of 21 rounded up, that is \left \lceil\frac{21}{2}\right \rceil. This time by simplifying we have:
From which, putting it into (6):
Therefore we obtain the analogue of (5):
Generalizing this development, in a way to let it valid for both even and odd numbers, you can obtain, starting from an integer x (respectively 20 and 21 in (5) and (5′)), the following overestimation of the products of prime numbers between \left \lceil\frac{x}{2}\right \rceil + 1 and x:
Remind that \left \lceil\frac{x}{2}\right \rceil is half of x rounded up, but it’s simply half of x if x is even.
Let’s move to the second point now. Starting from (7), it’s necessary to obtain an overestimation for the complete product of prime numbers up to x:
This product can be written as the product of prime numbers between \left \lceil\frac{x}{2}\right \rceil + 1 and x, multiplied by the product of those ones between 1 and \left \lceil\frac{x}{2}\right \rceil:
The product right after the equal sign is given by (7), so:
At this point, for the last product we can apply again (7) with \left \lceil\frac{x}{2}\right \rceil in place of x, obtaining an overestimation of the product of prime numbers between \left \lceil\frac{\left \lceil\frac{x}{2}\right \rceil}{2}\right \rceil + 1 and \left \lceil\frac{x}{2}\right \rceil. By iterating this procedure we obtain:
This procedure must terminate because, continuing to divide by two, at some point we’ll get to 1 or 2, and at that point it does not make sense continue dividing anymore, because the products of primes up to 2 (that is 2 itself) and up to 1 (that is 1) are known: they are the trivial cases of the \theta^{\star} function, that we discussed initially.
For example, for x = 21 we have:
where \binom{2}{1} = 2: at this point it does not make sense to continue; even if we did, we would obtain a product of 1 multiplied by itself infinite times, that does not affect the estimate (9) in any way.
Now the third point is left, that is simplifying (8) and (9) by replacing the binomial with an expression more simple to use in calculations. In particular, we’ll use Property N.1, that is
The details about how this formula is obtained are in the post Binomial estimates. Here, however, we are not interested in how to get to the formula, but it’s enough to place it in (8) and (9) in order to obtain more simple estimations of \theta^{\star}(x). For simplicity, we’ll proceed with the numerical example of x = 21:
You can note that, for passing from an exponent to the next one, it’s necessary to divide by two and round down: 10 = \left \lfloor \frac{20}{2} \right \rfloor, 5 = \left \lfloor \frac{10}{2} \right \rfloor, 2 = \left \lfloor \frac{5}{2} \right \rfloor and finally 1 = \left \lfloor \frac{2}{2} \right \rfloor. In particular, no exponent can exceed half of the previous one: 10 \leq \frac{20}{2}, 5 \leq \frac{10}{2}, 2 \leq \frac{5}{2} and finally 1 \leq \frac{2}{2}. This is a consequence of the kind of binomials we are using, given by (8). For example, the first binomial is \binom{21}{11} = \binom{x}{\left\lceil\frac{x}{2}\right\rceil}, from which the first two exponents are originated: 20 = 21 - 1 = x - 1 e 10 = 11 - 1 = \left\lceil\frac{x}{2}\right\rceil - 1. The second exponent \left\lceil\frac{x}{2}\right\rceil - 1 cannot exceed \left(\frac{x}{2} + \frac{1}{2}\right) - 1, because x is an integer and so, by rounding up \frac{x}{2}, we can add no more than \frac{1}{2}. But \left(\frac{x}{2} + \frac{1}{2}\right) - 1 = \frac{x}{2} - \frac{1}{2} = \frac{x-1}{2}, that is half of the first exponent indeed. This proves that the second exponent cannot exceed half of the first one, and this mechanism remains valid for all the exponents: in the same way you can prove that the third exponent cannot exceed half of the second one, that is one quarter of the first one, and so on:
So we can extend (10) with an additional inequality:
This argument can be easily generalized to a generic x:
Where the sum 1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\dots+\frac{1}{2^k} stops at the denominator 2^k that is the greatest power of two less than or equal to x-1. But, no matter how many terms of this series we consider, their sum will always be below a certain limit, indicated by \sum_{n=1}^{\infty} \frac{1}{2^n} and that we know to be 2:
The fact that this limit sum exists and is 2, is an easy application of the theory of numerical series. However, it’s easy to understand why the sum starting from the second term, \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\dots+\frac{1}{2^k}, cannot exceed 1 (from which it follows that the entire sum cannot exceed 2): it’s enough to imagine a segment of unitary length of which you cut half (that is \frac{1}{2}), then half of the remaining part (that is \frac{1}{4}), again a half, and so on: no matter how many times you cut, the sum of the fragments cannot exceed the length of the original segment, that is 1.
By putting (12) into (11) we obtain:
Finally we obtain the following estimate, an overestimation, of the product of primes up to x:
Majorization of the product of primes up to x
For all x > 0:
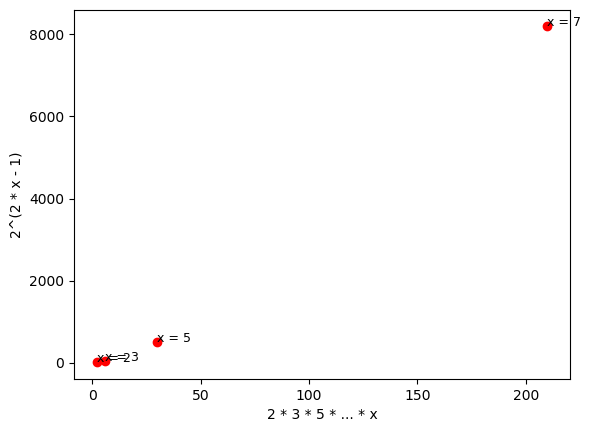
It’s interesting to note that the estimation given by Proposition N.1 cannot be considered good in practice: as you can see from the two charts below, one with the two axes at the same scale and the other one with different scales, the expression 2^{2(x-1)} has much higher values than the product of primes up to x, already for very small values of x.