Prerequirements:
In this post we’ll collect several properties of asymptotic orders which will be useful in the posts about number theory.
Meaning of equalities with asymptotic orders
Before seeing the properties of asymptotic orders, it’s worth clarifying some notations. In Definition A.3 we saw the meaning of asymptotic relationships of the kind
with X \in \{O, o, \Theta\}.
We can note that, in this kind of notation, the asymptotic order symbol X appears just after the equality symbol, alone. Equation (1), technically speaking, is not an equality, but it’s just an asymptitic relationship: it’s a way for writing that “f is an X of g“.
Many times it’s convenient to adopt another type of notation, apparently similar to (1), where the asymptotic relationship symbol appears also on the left of the equality symbol, for example:
In this case, the asymptotic relationship symbol which appears on the left of the equality stands for any function having that asymptotic order. So (2) means:
that is, all functions which are o(f) are also O(f) (by the way, this statement is true, as we’ll see in Property A.10, but now we are focusing just on notation).
We can note that the roles of asymptotic relationship symbols are very different depending on whether they appear on the right or on the left of the equality symbol:
- Those ones which appear on the right of the equality symbol must be understood according to Definition A.3;
- Those ones which appear on the left of the equality symbol must be understood as a function with that asymptotic order, with the universal quantifier (\forall).
So you have not to be misled by the presence of the equality symbol, which usually can be read indifferently from left to right or from right to left. For example, if we exchange the terms of (2), we’ll obtain the following asymptotic relationship:
which, though, has a very different meaning with respect to (2). It means, in fact (compare with (2′)):
that is, all functions which are O(f), according to these relationships, would also be o(f), and this statement is generally false.
Sometimes asymptotic relationship symbols appear on the right of the equality symbol, but not alone. In this case they stand for some function with that asymptotic order; but this time not any function, but a fixed one. For example, the following formula:
means:
Still in the case when on the right there is not an asymptotic order alone, other asymptotic orders may appear of the left. In that case all asymptotic orders represent some functions, you have to use the universal quantificator for the leftside orders and the existential one for the rightside orders, placing the universal quantifiers before existential ones. For example, the following formula:
means:
Summarizing, we can formulate the following definition:
Equalities with asymptotic orders
If in an equality there are some asymptotic orders (O, o or \Theta), it must be understood as follows:
- If on the right of the equality symbol there is an asymptotic order alone, the equality must be understood according to Definition A.3, and any asymptotic order on the left must be understood as a function with that asymptotic order, with the universal quantifier (\forall);
- If on the right of the equality symbol there is an asymptotic order and it’s not alone, but it’s part of an expression which optionally involves also other asymptotic orders, you must evaluate the following points in an orderly fashion:
- All the asymptotic orders on the left of the equality symbol must be understood as functions having those asymptotic orders, with the universal quantified (\forall)
- All the asymptotic orders on the right of the equality symbol must be understood as functions having those asymptotic orders, with the existential quantifier (\exists)
Let’s see some examples of the notation introduced with Definition A.8. Some of them match with the statements of some properties that we’ll see later in this post.
In the following table, we’ll assume f, g and h to be real functions, and a to be a real constant.
| Formula | Meaning | Case of Definition A.8 |
|---|---|---|
| -O(f) = O(f) | \forall g = O(f): -g = O(f) | 1 |
| a \cdot O(f) = O(f) | \forall g = O(f): a \cdot g = O(f) | 1 |
| O(f) g = O(fg) | \forall h = O(f): hg = O(fg) | 1 |
| x + O(x) = O(x) | \forall f = O(x): x + f = O(x) | 1 |
| 2x = x + O(x) | \exists f = O(x): 2x = x + f | 2 |
| x = O(x) + O(1) | \exists f = O(x) \exists g = O(1): x = f + g | 2 |
| O(x) = O(x) + O(x) | \forall f = O(x) \exists g = O(x) \exists h = O(x): f = g + h | 2 |
| O(x) + O(x) = O(x) | \forall f = O(x) \forall g = O(x): f + g = O(x) | 1 |
Properties with equalities
One function is a big Oh of its absolute value
Let f: I \rightarrow \mathbb{R}, where I is an upper unbounded subset of \mathbb{R}. Then:
By Definition A.3, f is O(|f|) if there is a constant A \in \mathbb{R} such that definitively |f(x)| \leq A |f(x)|. But such a constant A exists, in fact the previous inequality is true (not only definitively, but always) by putting A := 1. So f = O(|f|).
One simple corollary of this property is that, if f assumes only non-negative values, then f = O(f): in fact in this case f = |f| and so, by Property A.4, f = O(|f|) = O(f). But there is also a stronger result. In fact, it’s not necessary for the function to be always non-negative, but it’s sufficient to be definitively non-negative:
A definitively non-negative function is a big Oh of itself
Let f: I \rightarrow \mathbb{R} a definitively positive function, where I is an upper unbounded subset of \mathbb{R}. Then:
By Definition A.3, f is O(f) if there is a constant A \in \mathbb{R} such that definitively |f(x)| \leq A f(x). But f is definitively positive, so definitively we’ll have that |f(x)| = f(x), hence the condition |f(x)| \leq A f(x) is definitively satisfied with A := 1.
Still talking about absolute value, we can state the following Property:
The absolute value of a big Oh is still a big Oh
Let f: I \rightarrow \mathbb{R} a definitively positive function, where I is an upper unbounded subset of \mathbb{R}. Then, with the notation of Definition A.8:
We have to prove that, for every function g such that g = O(f), |g| = O(f). Being g = O(f), by Definition A.3 there exists a constant A such that definitively |g(x)| \leq A f(x). But ||g(x)|| = |g(x)| for all x, so also ||g(x)|| \leq A f(x) definitively. Then, again by Definition A.3, |g| = O(f).
If a function is a big Oh of another one, also its absolute value is such
Let f: I \rightarrow \mathbb{R} a function and g: I \rightarrow \mathbb{R} a definitively positive function, where I is an upper unbounded subset of \mathbb{R}. Then, with the notation of Definition A.8:
Since f = O(g), |f| = |O(g)| (in fact, the latter equality means that there exists a function h = O(g) such that |f| = |h|, but by hypothesis we can set h := f). But, by Property A.6, |O(g)| = O(g), so |f| = |O(g)| = O(g).
A function is O(1) if and only if it’s definitively bounded
Let f: I \rightarrow \mathbb{R}, where I is an upper unbounded subset of \mathbb{R}. Then:
By Definition A.3, f is O(1) when there exists a constant A such that definitively |f(x)| \leq A, that is -A \leq f(x) \leq A. So f is a definitively bounded function.
Conversely, if f is definitively bounded, there exist two constants B and C such that definitively B \leq f(x) \leq C. Let’s consider a value of x which satisfies this inequality and let’s prove that -A \leq |f(x)| \leq A, with A := \max(|B|, |C|). First of all, let’s note that this choice of A implies that -A \leq B and C \leq A. In fact:
- If B \geq 0, then -A = -\max(|B|, |C|) \leq 0 \leq B, so -A \leq B.
- If B \lt 0, then \max(|B|, |C|) = \max(-B, |C|) \geq -B, so -A = -\max(|B|, |C|) = -\max(-B, |C|) \leq B, hence -A \leq B in this case too.
- If C \lt 0, then C \leq 0 \leq \max(|B|, |C|) = A, so C \leq A.
- If C \geq 0, then C = |C| \leq \max(|B|, |C|) = A, so C \leq A in this case too.
So we’ll have that -A \leq B \leq f(x) \leq C \leq A, hence -A \leq f(x) \leq A. Now we can distinguish between two cases:
- If f(x) \geq 0, then f(x) = |f(x)|, so -A \leq f(x) \leq A \Rightarrow -A \leq |f(x)| \leq A.
- If f(x) \lt 0, then f(x) = -|f(x)|, so -A \leq f(x) \leq A \Rightarrow -A \leq -|f(x)| \leq A. But, changing the sign to the latter inequality, we’ll have that A \geq |f(x)| \geq -A, that is again -A \leq f(x) \leq A.
Summarizing, all the xes which satisfy the relationship B \leq f(x) \leq C, satisfy also the relationship -A \leq |f(x)| \leq A. So, since the first relationship is definitively true, also the second one is definitively true, so f = O(1).
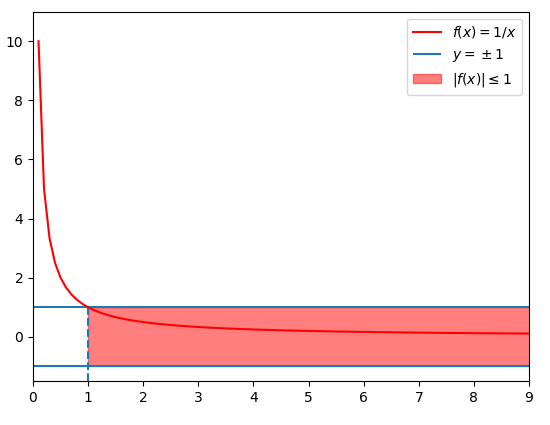
One example of a function which is O(1) is the function f(x) = \frac{1}{x}, defined on \mathbb{R}^{+}. In fact, for example, if x \geq 1 then |f(x)| \leq 1, so Definition A.3 is satisfied with A := 1. Then, by Property A.7, this function is definitively bounded, as you can see in the following picture. Note that, however, the function is unbounded: in fact it tends to infinity as x \to 0.
A simple consequence of Property A.7 is the case of constant functions. In fact, a constant function is obviously bounded (by itself), so it’s also definitively bounded, hence according to Property A.7 it’s O(1):
A constant function is O(1)
Let c: I \rightarrow \mathbb{R}, where I is an upper unbounded subset of \mathbb{R}, a constant function. Then:
Normally, in the mathematical language, a constant c \in \mathbb{R} tends to be identified with a constant function with value c (defined on a not specified domain, usually all \mathbb{R}). So it may happen to find the definition of c \in \mathbb{R} first, and then to find an application of the relationship c = O(1): in this case, a homonym function c: \mathbb{R} \rightarrow \mathbb{R} is implicitly defined, such that c(x) = c for all x \in \mathbb{R}.
The product of two big Oh is a big Oh of the product
Let f, g: I \rightarrow \mathbb{R} two definitively positive functions, where I is a right unbounded subset of \mathbb{R}. Then, with the notation of Definition A.8:
Let h = O(f) and k = O(g); we have to prove that hk = O(fg). By definition, there exist two real constants A and B such that, definitively, |h(x)| \leq A f(x) and |k(x)| \leq B g(x). Then, still definitively, |h(x)| |k(x)| \leq A B f(x) g(x) \Leftrightarrow |(hk)(x)| \leq AB (fg)(x), where (hk) and (fg) are the product functions respectively of h by k and of f by g. Then, being AB a real constant, hk = O(fg).
Product of a big Of by a definitively non-negative function
Let f, g: I \rightarrow \mathbb{R} two definitively positive functions, where I is a right unbounded subset of \mathbb{R} and g is definitively non-negative. Then, with the notation of Definition A.8:
By Property A.5, g = O(g). The thesis follows by applying Property A.8.
Product of a big Oh by a constant
Let f: I \rightarrow \mathbb{R} be a definitively positive function, where I is a right unbounded subset of \mathbb{R}; let c \in \mathbb{R}. Then, with the notation of Definition A.8:
By Corollary of Property A.7, c = O(1). The thesis follows by applying Property A.8.
A big Oh is invariant to sign change
Let f: I \rightarrow \mathbb{R} be a definitively positive function, where I is a right unbounded subset of \mathbb{R}. Then, with the notation of Definition A.8:
It’s enough to apply Corollary 2 of Property A.8, setting c := -1.
In the big Oh of a product of functions, a never null function can be moved outside
Let f,g: I \rightarrow \mathbb{R} be two definitively positive functions, where I is a right unbounded subset of \mathbb{R}. Let f(x) \neq 0 for all x \in I. Then, with the notation of Definition A.8:
We have to prove that, if h = O(fg), then there is a function k = O(g) such that h = fk.
If h = O(fg), then there is a constant A such that definitively |h(x)| \leq Af(x)g(x). Let’s divide this relationship by |f(x)| (we can do that because by hypothesis f(x) \neq 0): |\frac{h(x)}{f(x)}| \leq A\frac{f(x)}{|f(x)|}g(x). The ratio \frac{f(x)}{|f(x)|} is for all x either 1 or -1, so in particular it’s less than or equal to 1, hence definitively |\frac{h(x)}{f(x)}| \leq A g(x). This means that the function \frac{h}{f} is O(g). Moreover, h = f \cdot \frac{h}{f}, so \frac{h}{f} is the function k we were looking for.
This Property is only apparently similar to Corollary 1 of Property A.8. In fact, by Definition A.8, the statement of Property A.8A can be translated as:
Whereas the statement of Corollary 1 of Property A.8 can be translated into a very different formula:
A particular case of Property A.8A is when the function which is moved outside is a constant function (or a constant):
A big Oh of a function multiplied by a non-zero constant is a big Oh of the function
Let f: I \rightarrow \mathbb{R} be a definitively positive function, where I is a right unbounded subset of \mathbb{R}. Let c \in \mathbb{R}, c \gt 0. Then, with the notation of Definition A.8:
By Property A.8A, O(cf) = c \cdot O(f) and, by Corollary 2 of Property A.8, c \cdot O(f) = O(f).
The sum of two big Oh is a big Oh of the sum
Let f, g: I \rightarrow \mathbb{R} be two definitively positive functions, where I is a right unbounded subset of \mathbb{R}. Then, with the notation of Definition A.8:
We have to prove that, if k = O(f) and r = O(g), then k + r = O(f + g). Since k = O(f), there is a constant A such that definitively |k(x)| \leq Af; similarly, there is a constant B such that definitively |r(x)| \leq Bg. Then definitively |(k + r)(x)| = |k(x) + r(x)| \leq |k(x)| + |r(x)| \leq Af(x) + Bg(x) \leq \max(A, B)f(x) + \max(A, B)g(x) = \max(A,B) \cdot (f(x) + g(x)). So there is a constant C := \max(A, B) such that definitively |(k + r)(x)| \leq C(f(x) + g(x)), hence k + r = O(f + g).
A big Oh does not change by summing up it to itself
Let f: I \rightarrow \mathbb{R} be a definitively positive function, where I is a right unbounded subset of \mathbb{R}. Then, with the notation of Definition A.8:
It’s interesting to start with a wrong proof. We can note that O(f) + O(f) = 2 \cdot O(f), and the latter is O(f) by Corollary 2 of Property A.8. What’s wrong here is that the passage O(f) + O(f) = 2 \cdot O(f) assumes that the two O(f) on the left are the same function, but this assumption is false: they can be two different functions, though both O(f).
The correct proof is that, by Property A.9, O(f) + O(f) = O(f + f) = O(2f). Finally, by Corollary 1 of Property A.8A, O(2f) = O(f).
Property A.9 can be extended to any finite summation of definitively positive functions f_1, \ldots, f_n, for all n \geq 1. In fact the following relationship is true:
The proof consists simply in applying Property A.9 n - 1 times.
Relationships between big Oh and small oh
A small oh is also a big Oh
Let f, g: I \rightarrow \mathbb{R}, where I is a right unbounded subset of \mathbb{R} and g is definitively positive. Then, with the notation of Definition A.8:
This property is an immediate consequence of Definition A.3. In fact, by this Definition, f = o(g) if, for any positive real constant A, definitively |f(x)| \leq A g(x), whereas f = O(g) if there exists a positive real constant A for which the same relationship is true. Clearly the first condition implies the second, so if f = o(g) then f = O(g).
A big Oh of a big Oh is still a big Oh
Let f: I \rightarrow \mathbb{R} be a definitively positive function, where I is a right unbounded subset of \mathbb{R}. Then, with the notation of Definition A.8:
We have to prove that, if g = O(f) and h = O(g), then h = O(f). Since g = O(f), by Definition A.3 there is a constant A such that definitively |g(x)| \leq A f(x). Similarly, there is a constant B such that definitively |h(x)| \leq B g(x). Then definitively |h(x)| \leq B g(x) \leq |B| |g(x)| \leq |B| A f(x), so there is a constant C := |B| A such that definitively |h(x)| \leq C f(x), i.e. h = O(f).
A big Oh of a small oh is a small oh
Let f: I \rightarrow \mathbb{R} be a definitively positive function, where I is a right unbounded subset of \mathbb{R}. Then, with the notation of Definition A.8:
We have to prove that, if g = o(f) and h = O(g), then h = o(f). The latter asymptotical relationship, by Definition A.3, means that for every positive real constant A it’s definitively true that |h(x)| \leq A f(x). So, let’s fix a real constant A \gt 0 and let’s prove that |h(x)| \leq A f(x).
Again by Definition N.3, since h = O(g), there exists a positive real constant B such that definitively |h(x)| \leq B g(x); moreover, since g = o(f), for every positive real constant C it’s definitively true that |g(x)| \leq C f(x). Then, joining the inequalities, we’ll have definitively that |h(x)| \leq B g(x) \leq B |g(x)| \leq BC f(x). But, since C can be any constant, we can set C := \frac{A}{B}, in order to have that |h(x)| \leq BC f(x) = B \frac{A}{B} f(x) = A f(x), as we wanted to prove.
A small oh of a small oh is still a small oh
Let f: I \rightarrow \mathbb{R} be a definitively positive function, where I is a right unbounded subset of \mathbb{R}. Then, with the notation of Definition A.8:
We have to prove that, if g = o(f) and h = o(g), then h = o(f). The latter asymptotic relationship, by Definition A.3, means that for every positive real constant A it’s definitively true that |h(x)| \leq A f(x). So, let’s fix a real constant A \gt 0 and let’s prove that |h(x)| \leq A f(x).
Again by Definition N.3, since h = o(g), for every positive real constant B it’s definitively true that |h(x)| \leq B g(x); similarly, since g = o(f), for every positive real constant C it’s definitively true that |g(x)| \leq C f(x). So, joining the two inequalities, we’ll have definitively that |h(x)| \leq B g(x) \leq B |g(x)| \leq BC f(x). But, since B and C can be any constants, we can set B := C := \sqrt{A} (where \sqrt{A} is a positive real number because A \gt 0), in order to have that |h(x)| \leq BC f(x) = \sqrt{A} \sqrt{A} f(x) = A f(x), as we wanted to prove.
Properties with inequalities
Sometimes asymptotic orders appear also within inequalities. In this cases we’ll adopt the following convention:
Inequalities with asymptotic orders
If inside an inequality there are some asymptotic orders (O, o or \Theta), they must be understood as functions having those asymptotic orders, with the existential quantifier (\exists).
For example:
- f \leq O(g) means \exists h = O(g) \text{ such that } f \leq h
- O(g) \leq f means \exists h = O(g) \text{ such that } h \leq f
In addition we recall that, if we have two functions f and h defined on a set I, the notation f \leq h means that f(x) \leq h(x) for all x \in I.
In our posts about number theory, we’ll use the following properties of asymptotic orders with inequalities.
A function overestimated with absolute value by a big Oh is that big Oh
Let f, g: I \rightarrow \mathbb{R}, where I is a right unbounded subset of \mathbb{R} and g is definitively positive. Then, with the notation of Definitions A.8 and A.9:
If |f| \leq O(g), it means that there is a function h = O(g) such that |f| \leq h. Being h = O(g), there is a positive real constant A such that definitively |h(x)| \leq A g(x). But, for all x, |f(x)| \leq h(x) \leq |h(x)|, so definitively also |f(x)| \leq A g(x), that is f = O(g).
A function that lays between two equal big Ohs is that big Oh
Let f, g: I \rightarrow \mathbb{R}, where I is a right unbounded subset of \mathbb{R} and g is definitively positive. Then, with the notation of Definitions A.8 and A.9:
If O(g) \leq f \leq O(g), it means that there are two functions h = O(g) and k = O(g) such that h \leq f \leq k. Since h = O(g), there is a positive real constant A such that definitively |h(x)| \leq A g(x). Analogously, there is a positive real constant B such that definitively |k(x)| \leq B g(x). Now let’s consider an x such that both these relationships are satisfied. Let’s distinguish two cases:
- If f(x) \geq 0, then |f(x)| = f(x) \leq k(x) \leq |k(x)| \leq B g(x)
- If f(x) \lt 0, then |f(x)| = -f(x) \leq -h(x) \leq |h(x)| \leq A g(x)
So, by setting C := \max(A, B), we’ll have that definitively |f(x)| \leq C g(x), that is f = O(g).
If a function is definitively overestimated by a big Oh, than it always is
Let f, g: I \rightarrow \mathbb{R}, where I is a right unbounded subset of \mathbb{R} and g is definitively positive. Then, with the notation of Definitions A.8 and A.9:
If f(x) \leq \left(O(g)\right)(x) definitively, it means that there is a function h = O(g) such that f(x) \leq h(x) for all x \geq M, for some real constant M. We have to prove that f \leq O(g), i.e. that there is a function h^{\prime} = O(g) such that f(x) \leq h^{\prime}, for all x. Clearly when x \geq M we can take h^{\prime} = h, but we have to find a function that works with every x. For this purpose, let’s define the function h^{\prime} on I as follows:
This function is O(g) because definitively (for x \geq M) coincides with h, which is O(g). At the same time, f(x) \leq h^{\prime} for all x; in fact:
- If x \geq M, then h^{\prime}(x) = h(x) \geq f(x)
- If x \lt M, then h^{\prime}(x) = f(x) \geq f(x)
So f \leq h^{\prime}, with h^{\prime} = O(g), hence f \leq O(g).
A function overestimated by a big Oh of another function in turn overestimated by a third function, is a big Oh of the latter
Let f, g, h: I \rightarrow \mathbb{R}, where I is a right unbounded subset of \mathbb{R} and both g and h are definitively positive. Then, with the notation of Definitions A.8 and A.9:
If f \leq O(g), it means that there is a function g^{\prime} = O(g) such that f \leq g^{\prime}. Being g^{\prime} = O(g), there is a real positive constant A such that definitively |g^{\prime}(x)| \leq A g(x). Then, for every x which satisfies this relationship, f(x) \leq g^{\prime}(x) \leq |g^{\prime}(x)| \leq A g(x) \leq A h(x). But, by Corollary 2 of Property A.8, A h = O(h), so definitively f(x) \leq \left( O(h) \right) (x). Then, by Property A.14, f \leq O(h).
Properties with integrals
In the following Property, differently from the previous ones, when we’ll adopt the notation O(f) for indicating a real function g = O(f), we’ll suppose not only that g is defined on an upper unbounded subset of \mathbb{R}, but in addition we’ll suppose its domain to be an interval of the kind [a, +\infty), with a \in \mathbb{R}, and that g is integrable in every interval of the kind [a, b], with b \in \mathbb{R}. We need these additional hypotheses because the function O(f) will appear inside an integral function like \int_a^x O(f) dt. in fact, in order for this function to be well defined, the integrand function must be defined in the interval [a, +\infty) and must be integrable in every finite portion of it, of the kind [a, b]. We’ll omit the proof, which would be very technical and longer than those seen before.
The integral function of a big Oh is a big Oh of the function integral
Let f: I \rightarrow \mathbb{R} be a real, definitively positive function, where I is an upper unbounded subset of \mathbb{R}. Let a \in \mathbb{R}. Then, with the notations of Definition A.8:
where the x is the variable of the integral function, and O(f) stands for a function g: [a, +\infty) \rightarrow \mathbb{R} such that g = O(f) and g is integrable in every interval of the kind [a, b], with b \in \mathbb{R}.