Prerequirements:
- Chebyshev’s Theorem (weak version)
- From integer numbers to real numbers
- From integer numbers to real numbers – second part
- The factorial function and the \Lambda^{\star} function
- Properties of asymptotic orders
- Chebyshev’s Theorem (strong version)
- The functions W and V
- The integral mean value and the absolute error function R
- Some important summations
- The Möbius function and its connection with the function \Lambda
- The Möbius inversion formula
- Two lemmas with the Möbius function and the logarithm
After the digression about the Möbius function of the last three posts, let’s come back to the proof of the Prime Number Theorem. In this post we’ll see one of the most important parts of the proof, which consists in the application of Selberg’s Theorem. We’ll try to understand, with as few technicisms as possible, why this Theorem has a so important role in the proof of the Prime Number Theorem.
In Lemma N.7 we saw that a sufficient condition for proving the Prime Number Theorem is: \limsup_{u \to +\infty} |V(u)| = 0. In the post The integral mean value and the absolute error function R, we called \alpha this limit superior, and we began to compare it with the limit superior of the integral mean of the same function, i.e. with \beta := \limsup_{x \to +\infty} \frac{1}{\log x} \int_0^{\log x} |V(u)|\ du (see Definition N.14). So we asked ourselves if, without the limit superior, for every integer x \gt 0 the following relationship is true: |V(\log x)| \leq \frac{1}{\log x} \int_0^{\log x} |V(u)|\ du. By Lemma N.8, it’s equivalent to:
We saw that Selberg’s Theorem states an asymptotic relationship in which there are two terms similar to the two members of (1):
In this post we’ll see how we can get to this Theorem and how it’s used for proving the Prime Number Theorem. In order to answer these questions, we’ll use the knowledge about Möbius function.
How can we get to Selberg’s Theorem?
Selberg’s Theorem can be considered an intermediate result for arriving to formula (1), which, as we saw, is directly connected with the Prime Number Theorem.
From formula (1) we can obtain a similar formula, which is not equivalent but is simpler to be studied, by temporarily getting rid of the absolute value and the integral. This operation is convenient because:
- The absolute value will be reintroduced later, in Corollary 1 of Proposition N.8;
- The integral can be approximated by a summation, in this case of the kind \sum_{n \leq x} a_n R\left(\frac{x}{n}\right). This is the same principle we applied in the post From integer numbers to real numbers – second part, but in the opposite verse: in that case we needed to introduce integrals in order to apply the theorems of mathematical analysis; here instead we need to eliminate integrals, for trying to approximate an expression by a simpler one. Once we’ll have obtained a summation which approximates the initial integral, in the next post we’ll see how to estimate the error due to the approximation.
So, for the moment let’s set aside formula (1), while waiting for coming back to it in the next post, and let’s replace it with the following one:
With these simplifications, let’s develop the two terms of (1′) separately. About the left term, we’ll have that:
By using the definition of the function R and simplifying, we’ll have:
where we used the fact that, being x an integer number, \overline{\psi}(x) = \psi(x).
So, by Property N.6, \psi(x) = \sum_{n \leq x} \Lambda(n), we can see the term \psi(x) \log x in the light of the lemma of bar chart area, i.e. as the sum of all the bases of the rectangles, multiplied by the height of the last rectangle. By applying this Lemma with c_k := \Lambda(k), n := x and \widetilde{f}(t) := \log(t), we’ll obtain:
hence:
By Theorem N.4, \psi(x) \asymp x, so also \overline{\psi}(t) \asymp t. Then, by Definition A.1, \overline{\psi}(t) = O(t) and so, by Property A.8A, \frac{\overline{\psi}(t)}{t} = O(1) (we saw also Theorem N.7, which says more about the function \frac{\overline{\psi}(t)}{t}, but here it’s sufficient to know that it’s O(1)). Substituting into (b), we’ll have:
In the last passage we applied Property A.15, because the function \frac{\overline{\psi}(t)}{t} is defined in the interval [1, +\infty) and is integrable in every interval of the kind [1, b], with b \gt 1. The integrability in [1, b], in particular, is true because the function \frac{\overline{\psi}(t)}{t} can be discontinuous only for the ts where the function \overline{\psi}(t) is discontinuous, and this can happen only if t is an integer number. But there is a finite number of integers in a bounded interval like [1, b], so the function can have at most a finite number of discontinuities in [1, b], so it’s integrable there.
Finally, by joining formulas (a), (b) and (c) we’ll obtain (3).
Regarding the right term of (1′), we’ve said that we’ll approximate it by a summation of the kind \sum_{n \leq x} a_n R\left(\frac{x}{n}\right). In order to see what coefficients a_n are more suitable, let’s do some passages:
Now it makes sense to choose a_n := \Lambda(n), because:
- By Property N.6, the functions \Lambda and \psi are tightly connected, and this can be useful for simplifying the summation \sum_{n \leq x} a_n \overline{\psi} \left( \frac{x}{n} \right) = \sum_{n \leq x} \Lambda(n) \overline{\psi} \left( \frac{x}{n} \right);
- The summation \sum_{n \leq x} \frac{a_n}{n} = \sum_{n \leq x} \frac{\Lambda(n)}{n} can be estimated, by the Corollary of Proposition N.7, as \log x + O(1).
Making this substitution into (4), we’ll have:
where in the last two passages we applied Corollary 1 of Property A.8 first, and then Property N.20.
We can note that in both formulas (3) and (5) there is the term x \log x, which so can be eliminated by subtracting term by term (we’ll also apply the properties of asymptotic orders Corollary 3 of Property A.8 and Corollary of Property A.9):
Now the Möbius function comes into play, as it lets us rephrase these summations of \Lambda in a simpler way:
Third lemma about summations with the Möbius function and the logarithm
Let x be a positive integer. Then:
Let’s start from the first summation. By Property N.21, \sum_{nm \leq x} \Lambda(n) \Lambda(m) = \sum_{k \leq x} \sum_{nm = k} \Lambda(n) \Lambda(m). By exchanging the names of the variables n and k, we can write this summation as \sum_{n \leq x} \sum_{km = n} \Lambda(k) \Lambda(m). So we have to prove that:
It’s evident that the summation \sum_{n \leq x} is repeated for each term. So the strategy we’ll follow consists in proving (7′) without this summation, i.e. we’ll prove that, for all n \gt 0:
Clearly, if this inequality is true for all n, it’s also true after summing up each member for n = 1, \ldots, x, so (7′) is true, which is equivalent to (7).
So let’s prove (7”).
Starting from the left member, since we want to obtain as left member an expression which contains also the Möbius function and the logarithm, we have to apply the properties that let us to express the function \Lambda in terms of the other two functions. Let’s start with Property N.10 (logarithmic form), by which:
By applying Properties N.22 and N.23, it’s possible to make the internal summation such to have not d as index, but k:
Thus we have obtained the summation of the values of \Lambda for all the divisors of \frac{n}{d}, that by Property N.17 is equal to \log \frac{n}{d}:
where in the last passage we applied Property N.10 (logarithmic form) again.
Joining formulas (d), (e) and (f), we’ll obtain:
that is equivalent to (7”). This, as we pointed out initially, concludes the proof.
The interesting thing is that, as you can see in Figure 1, the function \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 d seems to be very similar to the function -x: if it was so, from (6) we would obtain that \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) - R(x) \log x = \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 d + O(x) = O(x) + O(x) = O(x), so:
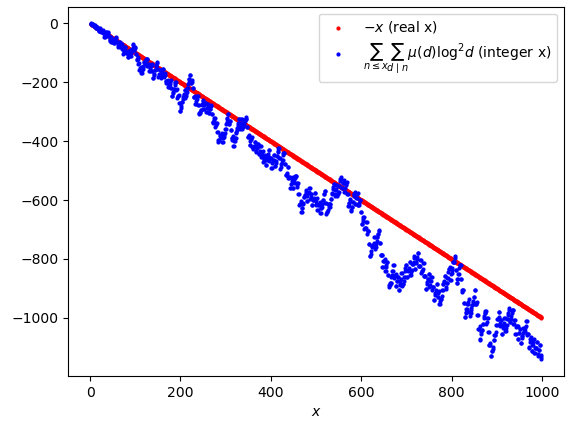
This relationship is identical to Selberg’s Theorem, expressed by formula (2), apart from the sign of the first term. We’ll see in a moment that we’ll not need to prove this relationship, however we think that it could be proved similarly to Lemmas N.9 and N.10, and we encourage whoever is able to find the proof to send it us.
The reason because we introduced formula (8), though it’s not really used in the proof of the Prime Number Theorem, is that it’s useful for understanding the main idea. In fact, rearranging the terms and applying Property A.6, the formula can be rephrased as follows:
Hence, introducing the absolute value, we can obtain a relationship which is identical to (1), except from the substitution of the integral by a summation:
Comparing the values of the integral (which for completeness’ sake we’ll represent for real values of x) with the ones of the summation, we can see that the approximation is not so bad:
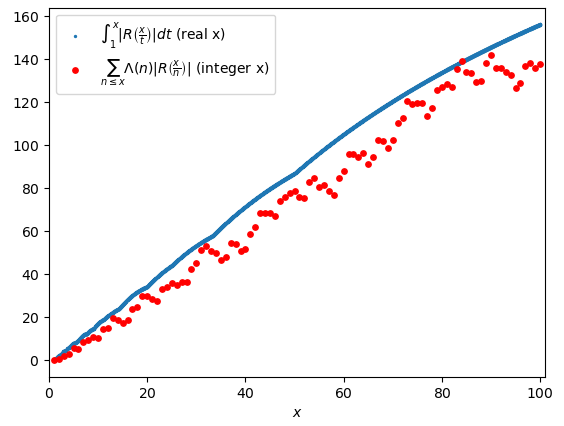
This may seem really a good result, which could let us proceed with the proof of the Prime Number Theorem; indeed, though, it’s not exactly so. The passages of the proof are very similar to these in their structure, but they are a little more complicated. In fact, we have to consider some aspects:
- Going on with the proof, as we’ll see in the next post, we’ll realize that, in order to proceed, we’ll need to multiply both members of (9) by \log x.
- Such a multiplication by the logarithm produces, in the right member, some new coefficients of R \left( \frac{x}{n} \right) the sum of which is just the left member of Lemma N.11, which in absolute value is less than or equal to \sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n. This is the reason why we don’t need to know the asymptotic order of the left member of Lemma N.11, i.e. the difference of the functions \sum_{nm \leq x} \Lambda(n) \Lambda(m) and \sum_{n \leq x} \Lambda(n) \log n, but we are interested in the asymptotic order of their sum.
- As well as the difference \sum_{nm \leq x} \Lambda(n) \Lambda(m) - \sum_{n \leq x} \Lambda(n) \log n in (6) comes from the difference \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) - R(x) \log x, the sum \sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n comes from the sum \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) + R(x) \log x. This justifies the introduction of Selberg’s Theorem, which states the asymptotic order of the latter sum, and so also of the sum \sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n.
Proof and application of Selberg’s Theorem
Rearranging everything, so, the main passages for continuing the proof of the Prime Number Theorem are the following:
- Proving the following Lemma:
Preliminary Lemma for Selberg’s Theorem
Let x be a positive integer. Then:
\sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n = \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left( \frac{n}{d} \right) \tag{10}As we did for Lemma N.11, we’ll prove the following inequality which is obtained from (10) by eliminating the summation \sum_{n \leq x}:
\sum_{km = n} \Lambda(k) \Lambda(m) + \Lambda(n) \log n = \sum_{d \mid n} \mu(d) \log^2 \left( \frac{n}{d} \right) \tag{10'}In order to compute the sum of \sum_{km = n} \Lambda(k) \Lambda(m) and \Lambda(n) \log n, we’ll trace it back to their difference, which by formula (7”) of the proof of Lemma N.11, is equal to \sum_{d \mid n} \mu(d) \log^2 d:
\begin{aligned} \sum_{km = n} \Lambda(k) \Lambda(m) + \Lambda(n) \log n & = \\ \sum_{km = n} \Lambda(k) \Lambda(m) - \Lambda(n) \log n + 2 \Lambda(n) \log n & = \text{[by (7'')]} \\ \sum_{d \mid n} \mu(d) \log^2 d + 2 \Lambda(n) \log n \end{aligned} \tag{g}As we already did in the proof of Lemma N.11, we’ll apply Property N.10 (logarithmic form) for obtaining an expression containing only the Möbius function and the logarithm:
\begin{aligned} \sum_{d \mid n} \mu(d) \log^2 d + 2 \Lambda(n) \log n &= \\ \sum_{d \mid n} \mu(d) \log^2 d + 2 \left( - \sum_{d \mid n} \mu(d) \log d \right) \log n &= \\ \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n) \end{aligned} \tag{h}We can note that \log^2 d - 2 \log d \log n are two out of three terms of the binomial square (\log d - \log n)^2 = \log^2 d - 2 \log d \log n + \log^2 n. The missing term, \log^2 n, does not depend on d, so, if it was included, it could be brought out from the summation \sum_{d \mid n} \mu(d). But this summation, if n \gt 1, by Property N.11, is equal to zero! This fact lets us complete the square of binomial, as follows:
\begin{aligned} \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n) &= \\ \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n) + \log^2 n \cdot 0 &= \text{[$n \gt 1$]} \\ \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n) + \log^2 n \cdot \left( \sum_{d \mid n} \mu(d) \right) &= \\ \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n) + \sum_{d \mid n} \mu(d) \log^2 n &= \\ \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n - \log^2 n) &= \\ \sum_{d \mid n} \mu(d) (\log d - \log n)^2 &= \\ \sum_{d \mid n} \mu(d) (\log n - \log d)^2 &= \\ \sum_{d \mid n} \mu(d) \log^2 \left( \frac{n}{d} \right) \end{aligned} \tag{i}The previous passages prove that \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n) = \sum_{d \mid n} \mu(d) \log^2 \left( \frac{n}{d} \right) for n \gt 1. For completeness’ sake, we have to prove the same thing for n = 1, considering that in such a case the only divisor of d is 1 itself:
\begin{aligned} n = 1 & \Rightarrow \\ \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n) &= \\ \mu(1) (\log^2 1 - 2 \log 1 \log 1) &= \\ \mu(1) \cdot 0 &= \\ \mu(1) \log^2 \left( \frac{1}{1} \right) &= \\ \sum_{d \mid n} \mu(d) \log^2 \left( \frac{n}{d} \right) \end{aligned} \tag{i'}Joining the previous formulas we’ll obtain (10′) and, similarly to the proof of Lemma N.11, reintroducing the summation \sum_{n \leq x} we’ll obtain (10).
-
On the basis of Lemma N.12, by applying Lemma N.10 we’ll obtain an asymptotic estimate of the sum \sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n:
Preliminary Lemma for Selberg’s Theorem: asymptotic estimate
Let x be a positive integer. Then:
\sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n = 2x \log x + O(x)The proof is based on the observation that the summation \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left( \frac{n}{d} \right) that appears in the statement of Lemma N.12 is very similar to the summation \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left( \frac{x}{d} \right) that we already know: in fact, by Lemma N.10, the latter is equal to 2x \log x + O(x).
Starting from formulas (i) and (i’) of the proof of Lemma N.12, modifying the latter formula into \sum_{d \mid n} \mu(d) \log^2 \left( \frac{x}{d} \right) (so with x instead of n in the logarithm argument) and replacing backwards \log x with \log n in all the proof, we’ll obtain the following alternative version of Lemma N.12:
\sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log x = \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left( \frac{x}{d} \right) \tag{l}In order to complete the proof of the present Lemma, so, all we have to do is to trace back the summation \sum_{n \leq x} \Lambda(n) \log x to the summation \sum_{n \leq x} \Lambda(n) \log n. For making so, let’s take again formulas (b) and (c) which appear in the detail below formula (3). Joining them we’ll obtain:
\psi(x) \log x = \sum_{n \leq x} \Lambda(n) \log n + O(x)But, by Property N.6, \psi(x) = \sum_{n \leq x} \Lambda(n), hence:
\sum_{n \leq x} \Lambda(n) \log x = \sum_{n \leq x} \Lambda(n) \log n + O(x)So, this is the connection between the summations \sum_{n \leq x} \Lambda(n) \log n and \sum_{n \leq x} \Lambda(n) \log x.
Substituting into formula (l), we’ll obtain:\sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n + O(x) = \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left( \frac{x}{d} \right)Finally, by applying Corollary 3 of Property A.8 and Lemma N.10, we can conclude the proof:
\begin{aligned} \sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n & = \\ \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left( \frac{x}{d} \right) + O(x) & = \\ 2x \log x + O(x) \end{aligned} - On the basis of Lemma N.13 we can prove Selberg’s Theorem. For convenience, we’ll propose again its statement here:
Selberg’s Theorem
R(x) \log x + \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) = O(x)By summing up member by member formulas (3) and (5) and applying Corollary of Property A.9, we’ll have:
\begin{aligned} R(x) \log x + \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) &= \\ \sum_{n \leq x} \Lambda(n) \log n - x \log x + O(x) + \sum_{nm \leq x} \Lambda(n) \Lambda(m) - x \log x + O(x) &= \\ \sum_{n \leq x} \Lambda(n) \log n + \sum_{nm \leq x} \Lambda(n) \Lambda(m) - 2x \log x + O(x) \end{aligned}By applying Lemma N.13 and again Corollary of Property A.9, we’ll have:
\begin{aligned} \sum_{n \leq x} \Lambda(n) \log n + \sum_{nm \leq x} \Lambda(n) \Lambda(m) - 2x \log x + O(x) &= \\ 2x \log x + O(x) - 2x \log x + O(x) &= \\ O(x) \end{aligned}Joining the two previous formulas we’ll obtain the thesis.
- On the basis of Selberg’s Theorem, we can prove the following Proposition:
Consequence of Selberg’s Theorem
R(x) \log^2 x = O(x \log x) + \sum_{n \leq x} \left( \sum_{km = n} \Lambda(k) \Lambda(m) - \Lambda(n) \log n \right) R\left(\frac{x}{n} \right) \tag{11}The proof is based on a play of sums and subtractions which, starting from R(x) \log^2 x, let us apply Selberg’s Theorem repeatedly, building each time the missing term:
\begin{aligned} R(x) \log^2 x &= \\ \log x (R(x) \log x) &= \\ \log x \left( R(x) \log x + \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \right) - \log x \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) &= \text{[Selberg's Theorem]} \\ \log x \cdot O(x) - \log x \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) &= \\ \log x \cdot O(x) - \sum_{n \leq x} \left( \Lambda(n) R\left(\frac{x}{n}\right) \log x \right) &= \\ \log x \cdot O(x) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) (\log x - \log n + \log n) &= \\ \log x \cdot O(x) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log \left( \frac{x}{n} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n \tag{m} \end{aligned}Now let’s focus on the expression R\left(\frac{x}{n}\right) \log \left( \frac{x}{n} \right) which appears in the central summation. We can set y := \frac{x}{n} obtaining R(y) \log y, an expression which could be extended like in the second equality above, obtaining R(y) \log y + \sum_{n \leq y} \Lambda(n) R\left(\frac{y}{n}\right), letting us apply Selberg’s Theorem again. The only problem is that the summation \sum_{n \leq y} is defined when y is an integer number, but y = \frac{x}{n} is not necessarily such. So we could set y := \left \lfloor \frac{x}{n} \right \rfloor, making an error of:
R\left(\frac{x}{n}\right) \log \left( \frac{x}{n} \right) - R \left( \left \lfloor \frac{x}{n} \right \rfloor \right) \log \left \lfloor \frac{x}{n} \right \rfloorHere we have a problem, because it’s not easy to estimate this error. But this problem is easily circumventable. Since our first posts up to now, we always supposed x to be an integer number, so we always worked with integers as far as possible, justifying the reasons why sometimes it’s convenient to move to real numbers. This is another example of when such a change is required: if for any reason it happens that the number x is divided by another integer n which is not a divisor of it, the result is not an integer. So, the formulas we obtained so far could not be valid more, since they have been proved starting from the assumption that x is an integer. Indeed, fortunately, our formulas are still valid even when x is not an integer, provided that all the summations like:
\sum_{n \leq x}are interpreted as:
\sum_{n \leq \left \lfloor x \right \rfloor}with the assumption that x \geq 1.
In order to be sure that we can interpret summations in such a way, in principle we should recheck all the proofs, but we’ll limit ourselves to a single example for understanding the concept. The proof of formula (3) begins with these passages:
\begin{aligned} R(x) \log x & = \\ (\overline{\psi}(x) - x) \log x & = \\ \overline{\psi}(x) \log x - x \log x \end{aligned}If x is not an integer, the last expression is no more equal to \psi(x) \log x - x \log x, as we saw before, but it’s equal to \psi(\left \lfloor x \right \rfloor) \log x - x \log x. Propagating this change into the proof of formula (3), the integer part of x will move just into the summation \sum_{n \leq x} \Lambda(n) \log n, which therefore will become \sum_{n \leq \left \lfloor x \right \rfloor} \Lambda(n) \log n. The same argument applies also to all the next statements, including Selberg’s Theorem, which for a real number t \geq 1 (where t is the argument of the function R, defined in [1, +\infty)) becomes:
R(t) \log t + \sum_{n \leq \left \lfloor t \right \rfloor} \Lambda(n) R\left(\frac{t}{n}\right) = O(t) \tag{n}By applying this “empowered” version of Selberg’s Theorem to the expression R\left(\frac{x}{n}\right) \log \left( \frac{x}{n} \right), setting t := \frac{x}{n}, we’ll have:
\begin{aligned} R\left(\frac{x}{n}\right) \log \left( \frac{x}{n} \right) &= \\ R\left(\frac{x}{n}\right) \log \left( \frac{x}{n} \right) + \sum_{m \leq \left \lfloor \frac{x}{n} \right \rfloor} \Lambda(m) R\left(\frac{x}{n} / m \right) - \sum_{m \leq \left \lfloor \frac{x}{n} \right \rfloor} \Lambda(m) R\left(\frac{x}{n} / m \right) &= \text{[by (n)]}\\ O\left( \frac{x}{n} \right) - \sum_{m \leq \left \lfloor \frac{x}{n} \right \rfloor} \Lambda(m) R\left(\frac{x}{nm} \right) \end{aligned}Substituting into (m), we’ll obtain:
\begin{aligned} \log x \cdot O(x) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log \left( \frac{x}{n} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n &= \\ \log x \cdot O(x) - \sum_{n \leq x} \Lambda(n) \left( O\left( \frac{x}{n} \right) - \sum_{m \leq \left \lfloor \frac{x}{n} \right \rfloor} \Lambda(m) R\left(\frac{x}{nm} \right) \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n &= \\ \log x \cdot O(x) - \sum_{n \leq x} \Lambda(n) O\left( \frac{x}{n} \right) + \sum_{n \leq x} \sum_{m \leq \left \lfloor \frac{x}{n} \right \rfloor} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n &= \end{aligned} \tag{o}By Property N.20, \sum_{n \leq x} \sum_{m \leq \left \lfloor \frac{x}{n} \right \rfloor} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right) = \sum_{nm \leq x} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right). Moreover, by the properties of asymptotic orders Property A.8A, Corollary 1 of Property A.8 and Corollary of Property A.9, \sum_{n \leq x} \Lambda(n) O\left( \frac{x}{n} \right) = x \cdot \sum_{n \leq x} \Lambda(n) O\left( \frac{1}{n} \right) = x \cdot \sum_{n \leq x} O\left( \frac{\Lambda(n)}{n} \right) = x \cdot O\left( \sum_{n \leq x} \frac{\Lambda(n)}{n} \right) . So, the next passage is:
\log x \cdot O(x) - x \cdot O\left( \sum_{n \leq x} \frac{\Lambda(n)}{n} \right) + \sum_{nm \leq x} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n =But, by Corollary of Proposition N.7, \sum_{n \leq x} \frac{\Lambda(n)}{n} = \log x + O(1), hence O\left( \sum_{n \leq x} \frac{\Lambda(n)}{n} \right) = O\left( \log x + O(1) \right). Applying sequentially the properties of asymptotic orders A.5, A.10, Corollary of Property A.9 and Property A.11, the last asymptotic order is equal to O(O(\log x) + O(1)) = O(O(\log x) + o(\log x)) = O(O(\log x) + O(\log x)) = O(O(\log x)) = O(\log x), so we’ll obtain:
\begin{aligned} \log x \cdot O(x) - x \cdot O(\log x) + \sum_{nm \leq x} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n &= \\ O(x \log x) - O(x \log x) + \sum_{nm \leq x} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n &= \\ O(x \log x) + \sum_{nm \leq x} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n \end{aligned}where we simplified asymptotic orders by means of the properties Corollary 1 of Property A.8, Corollary 3 of Property A.8 and Corollary of Property A.9.
By Property N.21, the summation \sum_{nm \leq x} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right) (that, renaming n into k, is equal to \sum_{km \leq x} \Lambda(k) \Lambda(m) R\left(\frac{x}{km} \right)), can be rewritten as \sum_{n \leq x} \sum_{km = n} \Lambda(k) \Lambda(m) R\left(\frac{x}{n} \right), so we’ll have finally:\begin{aligned} O(x \log x) + \sum_{n \leq x} \sum_{km = n} \Lambda(k) \Lambda(m) R\left(\frac{x}{n} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n &= \\ O(x \log x) + \sum_{n \leq x} \left( \sum_{km = n} \Lambda(k) \Lambda(m) - \Lambda(n) \log n \right) R\left(\frac{x}{n}\right) \end{aligned}Now, joining formula (m) with formula (o) and the next ones, we’ll obtain the thesis.
- By applying the absolute value to both members of (11), we’ll obtain the following Corollary:
Consequence of Selberg’s Theorem
|R(x)| \log^2 x \leq \sum_{n \leq x} \left(\sum_{km = n} \Lambda(k) \Lambda(m) + \Lambda(n) \log n\right) \left|R\left(\frac{x}{n}\right)\right| + O(x)By applying the absolute value to both members of (11), by the triangle inequality we’ll have:
\begin{aligned} |R(x)| \log^2 x & \leq \\ |O(x \log x)| + \left| \sum_{n \leq x} \left( \sum_{km = n} \Lambda(k) \Lambda(m) - \Lambda(n) \log n \right) R\left(\frac{x}{n} \right) \right| & \leq \\ O(x \log x) + \sum_{n \leq x} \left| \sum_{km = n} \Lambda(k) \Lambda(m) - \Lambda(n) \log n \right| \left| R\left(\frac{x}{n}\right) \right| & \leq \\ O(x \log x) + \sum_{n \leq x} \left( \left| \sum_{km = n} \Lambda(k) \Lambda(m) \right| + \left| - \Lambda(n) \log n \right| \right) \left| R\left(\frac{x}{n} \right) \right| &= \\ O(x \log x) + \sum_{n \leq x} \left( \sum_{km = n} \Lambda(k) \Lambda(m) + \Lambda(n) \log n \right) \left| R\left(\frac{x}{n} \right) \right| \end{aligned}where in the second equality we applied Property A.6 and in the last passage we considered that \Lambda is a non-negative function and logarithm does not assume negative values too, since n \geq 1. Concatenating the previous formulas, we’ll obtain the thesis.
- We can note that the sum of the coefficients of \left|R\left(\frac{x}{n}\right)\right| in Proposition N.8, as n varies, is just the expression that appears in Lemma N.13, since \sum_{n \leq x} \left(\sum_{km = n} \Lambda(k) \Lambda(m) + \Lambda(n) \log n\right) = \sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n, by Property N.21. So, indicating the n-th coefficient with a_n, the previous Proposition can be stated in the following form:
Consequence of Selberg’s Theorem, second form
For every positive integer x, there are some real numbers a_1, \ldots, a_x such that \sum_{n \leq x} a_n = 2x \log x + O(x) and
|R(x)| \log^2 x \leq \sum_{n \leq x} a_n \left|R\left(\frac{x}{n}\right)\right| + O(x)
Now, in order to conclude our argument about the application of Selberg’s Theorem, we still have to answer two questions:
- Why, in the passage from Selberg’s Theorem (Theorem N.10) to Proposition N.8, did we multiply by \log x?
- If, as we saw in Figure 2, the summation \sum_{n \leq x} \Lambda(n) \left|R\left(\frac{x}{n}\right)\right| approximates well the integral \int_1^x \left| R\left(\frac{x}{t}\right) \right| dt, what integral is approximated by the summation which appears in the Corollaries of Proposition N.8?
We’ll answer this questions in the next post.