Prerequirements:
In the post Some important summations we introduced the summations extended to couples of variables the product of which divides a constant (Definition N.21); now we’ll see how the Möbius function lets simplify this kind of summations. Finally we’ll obtain a very important formula, called Möbius inversion formula.
Simplification of double summations by means of the Möbius function
In the post Some important summations we saw the following Property, which for convenience we’ll write down also here:
Third equivalent form for summations where the product of indexes divides a constant
Let n be a positive integer number. Let f be any function defined on \mathbb{N}^{\star} \times \mathbb{N}^{\star} (the codomain does not matter(*)). Then:
(*) The same observations made about Property N.14 are also valid now
In spite of the apparent complexity, this Property is rather commonly used: the reason is that, in the double summation \sum_{d \mid n} \sum_{d^{\prime} \mid d} f\left(d^{\prime}, \frac{d}{d^{\prime}}\right), the inner summation may be something already known. Let’s take for example Property N.12 (logarithmic form):
If now we want to compute the summation:
we have to apply (1) by putting d in place of n, consequently choosing another name for the variable d, for example d^{\prime}:
Substituting into (2), we’ll have:
We have reduced to form (1), with f(x, y) := \mu(x) \log y. So we can apply Property N.15, obtaining:
So, roughly speaking, Property N.15 lets simplify double summations when the inner ones are created as an effect of substitutions.
But that’s not all. The summation we have obtained, in fact, can be simplified further. More generally, all summations like this can be simplified:
In fact, by gathering the terms with the same argument of the function f, and by using Property N.11, the following property can be proved:
Simplification, by means of the Möbius function, of a double summation extended to the divisors of a positive integer, and to the divisors of the divisors
Let n be a positive integer. Let f be any function defined on \mathbb{N}^{\star} (the codomain does not matter(*)). Then:
(*) The same observations made about Property N.13 are also valid now
An example of this Property, for n = 12, is illustrated in Figure 1, where, for each value of d, the summation \mu(d^{\prime}) f\left(\frac{d}{d^{\prime}}\right) is shown by arranging the values of f according to the Hasse diagram of d (recall that the Hasse diagram has been used in the previous post).
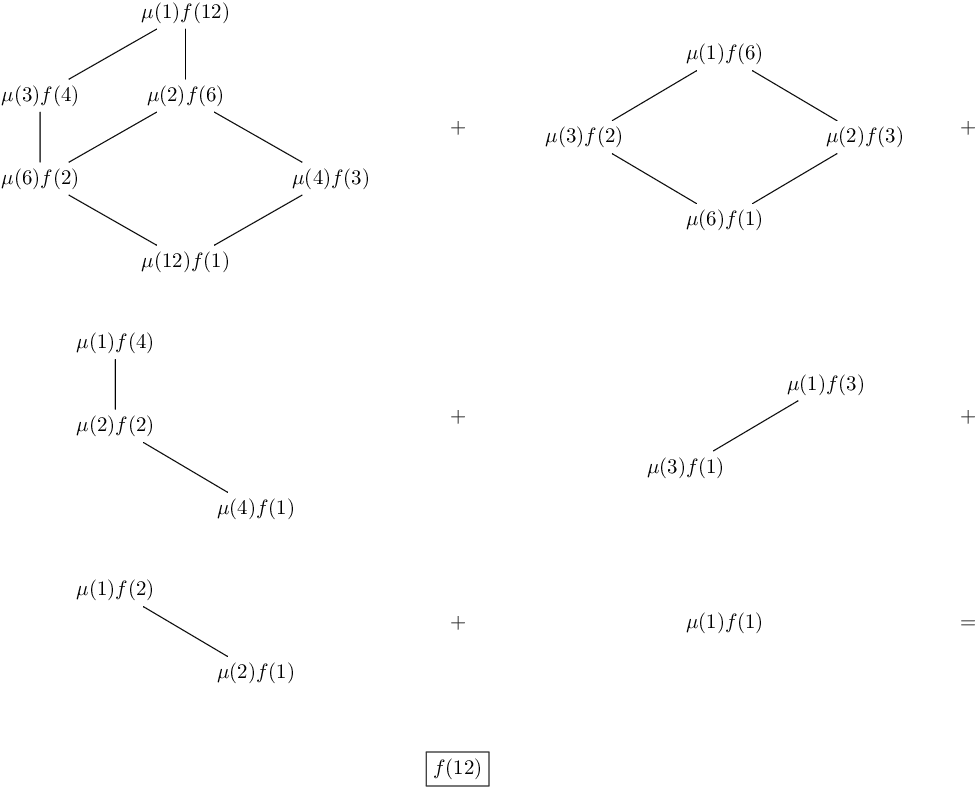
For n = 12, summation (4) becomes:
We can note that the same values of the function f are repeated many times, multiplicated by different values of \mu, so we can gather them. Doing so, each of them will be multiplied by a summation of values of \mu. For example, the value \boldsymbol{f(3)}, highlighted in bold, appears in three terms in which it’s multiplied respectively by \mu(4), \mu(2) and \mu(1), hence gathering these terms we’ll obtain \boldsymbol{f(3)}(\mu(1) + \mu(2) + \mu(4)).
Before proceeding with the simplification of (a), it’s useful to align the terms of different rows which have the same argument of the function f:
Now, in order to gather the repeated terms f(\cdot) we simply have to read this expression by columns instead of by rows. Doing so, we’ll obtain:
But, by Property N.11, all the summations of \mu(d) which we have obtained are zero, except for the last one which is 1, so the previous expression is reduced simply to f(12).
Like we did in the previous example, let’s gather in (5) all the terms of the kind f(b). First of all, the possible values of b are the divisors of n, by the relationship ab \mid n. In fact, from b \mid ab and ab \mid n it follows that b \mid n; moreover, if d is a divisor or n, we can set b := d and a := \frac{n}{d}, obtaining a couple of allowed values for the summation variables, because ab = \frac{n}{d} d = n, so ab \mid n).
So let’s fix a divisor d of n. Having established that d is one of the possible values of b, let’s ask ourselves now which are the summation terms with d as the value of the variable b. If the generic term of the summation is \mu(a) f(b), with ab \mid n, we have to look for all the values of a which generate terms of the kind \mu(a) f(d). Such a term appears in the summation if and only if ad \mid n, hence a \mid \frac{n}{d}. So, setting b := d, all the possible values of a are the divisors of \frac{n}{d}. Doing so, as d varies, we’ll exhaust all the summation terms, hence:
In the inner summation, we have gathered all the terms with f(d). The next step is to apply the distributive property:
By Property N.11, the inner summation is always zero, except when \frac{n}{d} = 1, that is when d = n. So:
By joining all the previous equalities, we’ll obtain (5).
Property N.16 is one of the reasons for which sums in number theory are more used than products: in fact, differently from Properties N.10 and N.12, there isn’t a product version of this Property (the reason is that the proof is based on Property N.11, which in turn exists only with sum).
From formula (3), by applying Property N.16 with f := \log, we can obtain immediately a new property of the function \Lambda:
Expression of logarithm as a summation of \Lambda
Let n be a positive integer. Then:
This Property is a sample application of the Möbius function: the knowledge of this function and its properties allowed us to obtain it immediately, otherwise we should have proved it separately.
The Möbius inversion formula
Comparing formulas (1) and (6), we can note that they are one the inverse of the other, meaning that:
- in the first formula, the function \Lambda is expressed as a summation of logarithms (with appropriate coefficients given by the Möbius function);
- in the second formula, the logarithm is expressed as a summation of the function \Lambda.
Since the passage from one formula to the other one is based on the properties of \mu, not of \Lambda, the same thing can be true for any function. Indeed, Properties N.15 and N.16 can be joined into a single one, called Möbius inversion formula (even if, rather than a formula, it’s a way for obtaining one formula from another):
Möbius inversion formula
Let n be a positive integer. Let f be any function defined on \mathbb{N}^{\star} (the codomain does not matter(*)), and let g be the function defined for all n \in \mathbb{N}^{\star} as follows:
Then
for all n \in \mathbb{N}^{\star}.
(*) The same observations made about Property N.13 are also valid now
In order to prove that
we have to substitute into this equality the definition of g, obtaining:
The thesis follows by applying the Properties N.15 and N.16:
By Property N.14, the definition of the function g can be also expressed in the following form, perhaps easier to remember: