Prerequirements:
- Row computation for third order linear dashed lines
- Computation of a dash value in a linear second order dashed line
- Row computation and differences between dash values
In order to compute the x-th dash value for a third order linear dashed line, we can act similarly to how we did for the second order. The general approach is still based on downcast; but now we have two possibilities: we can do the downcast from the third order to the second one (that is from T to T[i, j], where T = (n_1, n_2, n_3) is the given dashed line), or from the third order to the first one (that is from T to T[i]). Both possibilities are illustrated below:
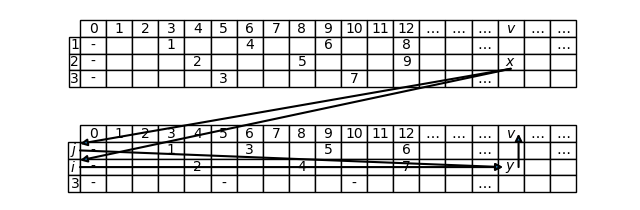
In both cases, since formulas for row computation are already known, only the respective downcast characteristic equations remain to be solved, in order to compute, using the symbols of Figures 1 and 2, the ordinal y starting from the ordinal x. We’ll see that, depending on whether the downcast is made to the second order or to the first one, there are characteristic equations which differ not only in form, but also in substance, so it’s convenient to treat the two cases separately.
Computation of linear \mathrm{t\_value} by means of a downcast from the third order to the second one
Let’s resume the downcast characteristic equation of linear \mathrm{t} from the third order to the second one, given by Corollary 3 of Proposition T.4, in its compact form:
We point out that:
- U = T[i, j] is a second order dashed subline containing row i which contains the x-th dash of the initial dashed line T
- k is the index of the only row not belonging to U
- \mathrm{t\_value}_U is a second order \mathrm{t\_value} function, and as such it can be computed thanks to Theorem T.8 (Formula for computing the second order linear \mathrm{t\_value} function)
The solution of the equation, in the unknown y, is given by the following Theorem:
Solution of the downcast characteristic equation of linear \mathrm{t}, from the third order to the second one
Let T be a linear third order dashed line, with indexes I = \{1, 2, 3\} = \{i, j, k\}. Let \mathrm{t}_T(x) \in T[i]. Then the ordinal y such that \mathrm{t}_T(x) = \mathrm{t}_{T[i,j]}(y), solution of equation (1), is given by the following function d_{i,j}: \mathbb{N}^{\star} \rightarrow \mathbb{N}^{\star}:
In particular:
For the proof of this Theorem, see Teoria dei tratteggi (Dashed line theory, in Italian), pages 178-179.
If we compare the statement of this Theorem with the one of the corresponding Theorem for the second order, Theorem T.7, we can note that the function defined in the latter, d_i(x), is called downcast function, whereas in Theorem T.9 it’s not the same for the function d_{i,j}(x). Indeed the latter is not properly a downcast function from T to T[i,j]. In fact, though computing the ordinal y starting from the ordinal x, it does not do it in all cases, but only when x is an ordinal of row i: in fact in Theorem T.9 there is the hypothesis that \mathrm{t}_T(x) \in T[i]. If d_{i,j}(x) was a downcast function, it should “work” (i.e. compute the right y) also when \mathrm{t}_T(x) \in T[j], that is for all the ordinals x of the dashed subline T[i,j]. But it’s not difficult to find such a function. First of all, Theorem T.9 states that, if \mathrm{t}_T(x) \in T[i], the function d_{i,j}(x) can be used. If instead \mathrm{t}_T(x) \in T[j], Theorem T.9 can be rewritten exchanging the symbols i and j, obtaining a new statement according to which the function to be used is d_{j,i}(x), the definition of which is still given by (2), exchanging i and j. Thus a proper downcast function from T to T[i,j] is the one defined in the following Corollary.
Downcast function of linear \mathrm{t}, from the third order to the second one
Let T be a linear third order dashed line, with indexes I = \{1, 2, 3\} = \{i, j, k\}. Then the following function d_{i,j}: \mathbb{N}^{\star} \rightarrow \mathbb{N}^{\star}:
is a downcast function of linear \mathrm{t}, from T to T[i,j].
We can note that the two cases of the definition of d_{\{i,j\}}(x) are identical, except for the condition that multiplies the polynomial n_i + n_j: this is in fact the only part of formula (2), from which each case is derived, that is not symmetrical with respect to i and j. Formula (4) instead has this property of symmetry: if you exchange i and j in it, the two cases get interchanged, but the function remains the same. If you think about it, things cannot be different, because making the downcast from T to T[i,j], or from T to T[j,i], is the same thing. In fact T[i,j] and T[j,i] denote the same dashed subline, they are two alternative notations (see the remark after the definition of dashed subline). On the contrary, this is not true for formula (2), because the hypothesis that the dash belongs to row i, and not j, makes different the roles of the two rows, and so is source of asymmetry.
For indicating the fact that the function d_{\{i,j\}}(x) is symmetrical with respect to i and j, we used the set notation \{i,j\} at the subscript, since in set theory \{i,j\} = \{j,i\}. Instead this kind of notation is missing in the function d_{i,j}(x), for indicating that it’s not symmetrical with respect to i and j.
Now all that remains to be done is to apply Theorem T.9 for computing the value of the x-th dash of the initial dashed line T. Provided that it belongs to row i, and recalling that we can know i thanks to Theorem T.4 (Computation of the row of the x-th dash for a third order linear dashed line with two by two coprime components)) or to Theorem T.6 (Row computation of the x-th dash in any third order linear dashed line), by Theorem T.9 we have that:
But if two dashes are equal, their values are equal too, so
Now the right member can be computed by applying Theorem T.8 (Formula for computing the second order linear \mathrm{t\_value} function). Applying this Theorem with T := T[i,j] (the latter plays the role of the second order dashed line that contains the dash the value of which is unknown) and x := d_{i,j}(x) (the dash ordinal with respect to the former dashed line), we’ll obtain that
Joining (6) with (5), we’ll obtain the following Theorem:
General formula for computing third order linear \mathrm{t\_value} function
Let T be a linear third order dashed line, with indexes I = \{1, 2, 3\} = \{i, j, k\}. Let i be the row of the x-th dash of T (computable by applying Theorem T.4 or Theorem T.6). Then:
where
- d_i(x) = \left \lceil \frac{n_j x + (j \gt i)}{n_i + n_j} \right \rceil is the function defined in Theorem T.7 (Solution of the downcast characteristic equation of linear \mathrm{t}, from the second to the first order)
- d_{i,j}(x) = \left \lceil \frac{(n_i + n_j)n_k x - n_i n_j + (k \gt i)(n_i + n_j)}{n_i n_j + n_i n_k + n_j n_k} \right \rceil is the function defined in Theorem T.9 (Solution of the downcast characteristic equation of linear \mathrm{t}, from the third order to the second one)
It’s important to become familiar with the following part of formula (7):
Here we have the composition of the function d_{i,j}, that is computed before and is referred to the dashed line T, with the function d_i, that is computed after and is referred to the dashed line T[i,j]. We said that the function d_{i,j} for the ordinals of row i behaves as a downcast function from T to T[i,j]. Moreover the function d_i is a downcast function from the dashed line which it’s referred to, i.e. T[i,j], to T[i]. So we have the following downcast chain:
Or simply:
Theorem T.10 is intentionally abstract, in the sense that it does not specify a value for i, j and k: it’s because this way the single formula (7) can express six different formulas. In fact i can be 1, 2, or 3; in addition, for each choice of i, we are free to choose j between the two remaining indexes; for example if i is 1, j can be 2 or 3, according to the condition I = \{1, 2, 3\} = \{i, j, k\}. Only the choice of k is forced, because of the same condition, after i and j have been chosen. But each different triplet (i,j,k) leads to a different formula: this means that, for each choice of i, there are two different formulas that compute the same thing, that is the value of the x-th dash when it belongs to row i.
Summarizing, we have three possible choices of i, for each of them we have two possible choices for j, and for each choice of i and j we have a forced choice of k: so 3 \cdot 2 \cdot 1 = 6 possible choices, and 6 possible formulas. Six formulas may not seem many, but imagine what can happen generally. For a generic order k, the number of formulas would become, by the same argument, k \cdot (k-1) \cdot \ldots \cdot 2 \cdot 1 = k!. It’s a number growing so quickly that soon it would become impossible to list all possible formulas, even for small values of k. For this reason it makes sense to use a single generic formula, like (7), that includes all.
On the other hand, in practice it’s easier to apply “concrete” formulas, without too many variables. For meeting this need we can limit ourselves to what is really important, that is the value of i, and choose only one “canonical” formula for each value of i. We said that for the third order there are two different formulas for each value of i, according to the value we choose for j (or, if we prefer, for k). Between these two formulas we’ll choose, as canonical, the one obtained with the smallest possible value of j (or, equivalently, with the largest possible value of k). So we’ll make the following “canonical” choices:
| i | j | k | T \rightarrow T[i,j] \rightarrow T[i] |
|---|---|---|---|
| 1 | 2 | 3 | T \rightarrow T[1, 2] \rightarrow T[1] |
| 2 | 1 | 3 | T \rightarrow T[1, 2] \rightarrow T[2] |
| 3 | 1 | 2 | T \rightarrow T[1, 3] \rightarrow T[3] |
For each canonical choice we wrote the corresponding downcast chain. Recall that T[1,2] = T[2,1]: this is the reason why the intermediate dashed subline is the same for both the first choice ((i,j) = (1,2)) and for the second one ((i,j) = (2,1)).
Substituting the canonical choices in the statement of Theorem T.10, the following Corollary is obtained:
Canonical formulas for computing the third order linear \mathrm{t\_value} function
Let T be a third order linear dashed line, with indexes I = \{1, 2, 3\}. Let i be the row of the x-th dash of T (computable by applying Theorem T.4 or Theorem T.6). Then:
Keep in mind that, after having substituted the variables i, j and k in Theorem T.10, thus obtaining formula (8), we ordered the polynomial expressions in n_1, n_2 and n_3 with respect to the indexes of these variables. That’s why, for example, at the denominator of the most external fraction there is always n_1 n_2 + n_1 n_3 + n_2 n_3. This makes a bit more readable a formula like (8) that is already rather structurally complicated.
As an example we can resume the introductory post From a problem about jogging to dashed lines, where in the solution part we computed the value of the x-th dash of the dashed line (3,4,5), for x = 12. In the cited post we indicated this dash by (i, n), then we established that it belongs to the second row (that is i = 2), finally we computed n with the formula
The dash value was then obtained with the formula n_2 n = 4 n, that is
Let’s check this formula to coincide with (8). If in the latter we substitute, in the case i = 2, the values (n_1, n_2, n_3) = (3, 4, 5), we’ll obtain:
As we expected, the two formulas coincide. Substituting x = 12 and making the calculations, we can confirm the final result \mathrm{t\_value}_T(12) = 16.
Computation of \mathrm{t\_value} by means of a downcast from the third order to the first one
Let’s now focus our attention on the downcast characteristic equation of \mathrm{t} from the third order linear dashed line T to its first order dashed subline T[i]. We saw this equation in Corollary 2 of Proposition T.4 and for a matter of convenience we rewrite it here in its compact form:
Recall that the unknown y is the ordinal of the x-th dash of T within row i, i.e. y is such that
So the problem is directly reduced to a first order dashed line, and this lets compute the dash value immediately, without more downcasts… but there is a problem. Unfortunately a downcast function from the third order to the first one, that is a function which computes y for all x, is not yet known. For now there exists a function that computes the correct y value only in some cases (and for this reason we can’t call it a downcast function, as we pointed out before, about the d_{i,j} function):
Partial solution of the downcast characteristic equation of linear \mathrm{t}, from the third order to the first one
Let T be a linear third order dashed line, with indexes I = \{1, 2, 3\} = \{i, j, k\}. Let t := \mathrm{t}_T(x) \in T[i] be such that the difference between its value and the one of the previous dash of row k, difference that we call a, respect the following condition:
Then the ordinal y such that t = \mathrm{t}_{T[i]}(y), solution of equation (9), is given by the following function e_i: \mathbb{N}^{\star} \rightarrow \mathbb{N}^{\star}:
In particular:
This Theorem appears in the original work Teoria dei tratteggi (Dashed line theory, in Italian), pages 182-183, in a slightly different form, where in place of the hypothesis (10) there is the following one:
But this hypothesis, besides being more cryptic, has no practical importance, for it involves the number y that’s just the unknown to be computed: so we preferred the formulation of Theorem T.11. The original Theorem however turns out to be useful for the proof, because we can see Theorem T.11 as a modified version of the original Theorem, in which we replaced the hypothesis (12) with (10). At this point, so, for proving Theorem T.11 it’s sufficient to prove that the new hypothesis, (10), entails the old one, (12). This way we put ourselves in the condition of being able to apply the original Theorem, that was already proved, and that has the same conclusion as Theorem T.11, that is the validity of formula (11).
It may seem rather difficult to prove formula (12) starting from (10), but things change after the meaning of the modulus has been understood. This meaning is better highlighted if starting from (12) we pass to a stronger unequality:
It’s clear that (12′) implies (12), for n_i(n_j + n_k) \geq n_j \left( (n_i y - (k \gt i)) \mathrm{\ mod\ } n_k + (k \gt i) \right) \geq n_i(n_j + n_k) \geq n_j \left( (n_i y - (k \gt i)) \mathrm{\ mod\ } n_k \right), so if we prove that (12′) is true, we automaticcaly prove that (12) is true too. So let’s reason about (12′).
The key of the proof is to understand the meaning of the expression
The number n_i y is the value of the dash t (we called so the x-th dash of T). In fact in the statement of Theorem T.11 we said that it has ordinal y within row i and so, by Proposition T.1, its value is n_i y. So we can rewrite (13) as
where we indicated with |t| the value of t. Now the expression (14) assumes a very precise meaning: it represents the difference between the value of t and the one of the previous dash of row k, just the number that we indicated with the letter a:
Equality (15) is itself a Proposition to which we’ll devote one of the next posts. For the moment we go on taking formula (15) as true. So, substituting this formula back to (12′), we’ll obtain
So (10) is equivalent to (12′), which in turn, as we saw, implies (12), so also (10) implies (12). This completes the proof, because the original Theorem, with the hypothesis (12) in place of (10), was already proved in op. cit., pages 182-183.
We can rephrase hypothesis (10) this way:
Now it’s clear that Theorem T.11 requires the number a to be lower than a certain amount, that depends on the dashed line components. In less formal terms, we can say that the dashed t must not be “too distant” from the previous of row k.
We already talked about the number a in the post Row computation and differences between dash values. In particular, in Theorem T.5 (Difference between the value of a dash of a row and the one of the previous dashed of other rows, for a third order linear dashed line) we saw that, if the dashed line components are two by two coprime, this number a is such that
So we can compute a computing the left side modulus and expressing it in the form n_j a + n_k b in such a way to let it a member of R_T(i) (that means, in practice, to fix some limits on the possible values of a and b: see Theorem T.4 (Computation of the row of the x-th dash for a third order linear dashed line with two by two coprime components)). After computing a, by evaluating the condition (10) we’ll know if we can apply (11) for computing y (if (10) in not satisfied, formula (11) may return a wrong value for y).
It’s worth pointing out, however, that there is a case in which (10′), and so also (10), is always true: it’s when i is the index of the greatest dashed line component. In fact, being a the difference between the value of t and the one of the previous dash of another row, for example j, certainly a cannot exceed n_j (otherwise there would be at least n_j consecutive columns with no dashes with component n_j, that’s impossible). But if a is less than or equal to n_j, and if this is less than n_i, then a is less than n_i and so (10′) is true:
The same argument can be applied if the other row is n_k: nothing changes because it’s still a component less than n_i, which we supposed to be the greatest.
Summarizing, we can always use formula (11) for doing the downcast of linear \mathrm{t} from a third order dashed line to its row corresponding to the greatest component (tipically the last row), without need to evaluate (10), that is automatically true.
One of the most frequent themes of dashed line theory is symmetry, and also in this case we cannot do without speaking about it. We can note that formula (11) is perfectly symmetrical with respect to j and k: exchanging the two symbols, exactly the same formula is obtained. This makes sense bacause, when we do the downcast from a linear third order dashed line T to one of its rows T[i], no matter how we call the other two rows, which we call j and which k: it does not matter for the purpose of calculation. It may seem obvious, but it’s important to remark two things:
- The same thing is not true for Theorem T.9, where we make the downcast from T to T[i,j]. In this case, even if the x-th dash still belongs to row i, it’s important to distinguish between j and k, because only j makes part of the destination dashed subline. So the formula that solves the downcast characteristic equation from the third order to the second one, with the hypothesis of belonging to row i (formula (3)), could never be symmetrical with respect to j and k. The “trick”, if we want to call it so, for making it symmetrical, is to remove the hypothesis of belonging to row i, but we already talked about that (see the remark after Theorem T.9).
- Getting back to Theorem T.11, we can note that hypothesis (10) is not symmetrical with respect to j and k. This looks like a contradiction compared with what we said before, but there is certainly an explanation: for example formula (10) and the one obtained from it exchanging j and k:
n_i(n_j + n_k) \geq n_k a
may be equivalent. If they aren’t, certainly formula (11) gives the correct result when even only one of the two is true, because Theorem T.11 guarantees the correct result independently of the choice of j and k. There still remains the fact that condition (10), for its lack of symmetry, is a sign that the Theorem statement could be improved, but this is still an open point.
Does a version of Theorem T.11 without the additional hypothesis (10) exist? In other terms, is it possible to solve the downcast characteristic equation (9) for any ordinal x, given only the row which the dash belongs to? This question is still without an answer. A partial answer at the moment is given by the following hypothesis:
Range of possible values for a downcast function of linear \mathrm{t} from the third order to the first one
Let T be a linear third order dashed line, with indexes I = \{1, 2, 3\} = \{i, j, k\}. Let f_i a downcast function of \mathrm{t} from T to T[i]. Then the following equality is supposed to be true:
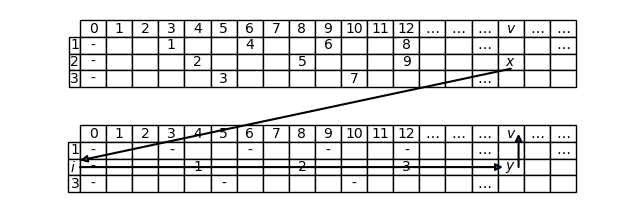
Let’s try to repeat the previous example by applying Theorem T.11 instead of Theorem T.9. We have to check if the Theorem can be applied, by evaluating if hypothesis (10) is satisfied. Writing the dashed line table we can see that the dashes which preceed the twelfth in the other rows have value 15, both on the first row and on the third one:

So in this case, no matter how we choose j and k ((j,k) = (1,3) or (j,k) = (3,1)), the number a is always 1. It’s a small number, in fact we can see that hypothesis (10) is satisfied. For example, choosing k = 3 we’ll have:
Since hypothesis (10) is satisfied, we can apply formula (11), so
Hence, by Proposition T.1 (Linear first order \mathrm{t} and \mathrm{t\_value} functions), \mathrm{t\_value}_T(12) = n_i y = 4 \cdot 4 = 16, as we obtained before.