Prerequisiti:
- Calcolo degli spazi nei tratteggi lineari di secondo ordine
- Principio di inclusione-esclusione (preferenziale)
Attualmente, la formula per calcolare \mathrm{t\_spazio} per un tratteggio lineare di ordine qualsiasi non è ancora nota, ma, come abbiamo visto nella parte di teoria dei tratteggi, esistono alcuni risultati parziali, che potrebbero portare, una volta estesi, a una formula generale. Le uniche formule già conosciute sono quella per i tratteggi del tipo (n_1) del primo ordine:
e per quelli del tipo (n_1, n_2) del secondo ordine:
dove S(T) è il numero di spazi in un periodo del tratteggio.
Proseguendo nell’articolo, vedremo come è possibile ragionare per ottenere una formula per gli ordini superiori al secondo, e quali sono le difficoltà che si incontrano. Proprio per via di tali difficoltà, ha senso anche ricercare una formula in grado di approssimare \mathrm{t\_spazio}, mantenendo un buon compromesso tra bontà dell’approssimazione e complessità della formula. A questa possibilità accenneremo nell’ultima parte dell’articolo.
Prima di procedere, vale la pena notare che un’altra possibile strada per cercare una formula valida indipendentemente dall’ordine è procedere per via indiretta. Dato che le formule per il calcolo di \mathrm{t\_spazio} diventano sempre più complesse man mano che l’ordine sale, si potrebbe adottare un approccio diverso: ossia, piuttosto che cercare una formula, determinare una caratterizzazione, ossia un criterio che ci indichi quali colonne sono spazi. Una volta trovata, il criterio ottenuto potrebbe essere usato come base per ricavare una formula vera e propria.
La ricerca di una caratterizzazione degli spazi che valga per tutti i tratteggi, indipendentemente dall’ordine, è una questione ancora aperta, ed è trattata in una pagina dedicata, in cui si possono trovare i progressi della nostra indagine in tal senso.
Come si può ragionare per ottenere un formula per \mathrm{t\_spazio}, per qualsiasi ordine
Anche se ancora non abbiamo una formula che calcola la funzione \mathrm{t\_spazio} per tratteggi lineari di ordine superiore al secondo, possiamo caratterizzarla come soluzione di un’equazione, come abbiamo fatto per il secondo ordine. Per ricavare quest’equazione, tuttavia, è necessario cambiare approccio: non basta, come abbiamo fatto per il secondo ordine, contare i trattini per colonne e per righe, ma dobbiamo ricorrere ad un principio matematico generale, noto come principio di inclusione-esclusione. Vediamo come applicarlo nel notro caso.
Siano T = (n_1, ..., n_k) un tratteggio lineare di ordine k > 1, x un intero positivo fissato, ed s := \mathrm{t\_spazio}_T(x). Essendo s l’x-esimo spazio di T, le prime s colonne di T si possono dividere in x spazi ed s - x colonne contenenti almeno un trattino. Il problema è ora contare queste colonne con una formula diversa, in modo che, come abbiamo fatto per il secondo ordine, uguagliando tale formula con s - x si possa ottenere un’equazione da cui ricavare s in funzione di x.
Per prima cosa, introduciamo una notazione che ci può essere utile: indichiamo con C(i) l’insieme delle colonne minori o uguali ad s che sono divisibili per n_i, per i = 1, \ldots, k. A noi interessa sapere quante sono le colonne minori o uguali ad s divisibili per almeno una componente, cioè quelle che appartengono ad almeno uno di questi k insiemi. Ma dire che una colonna appartiene ad almeno uno degli insiemi C(1), \ldots, C(k) equivale a dire che appartiene alla loro unione, C(1) \cup \ldots \cup C(k): questo è l’insieme delle colonne minori o uguali ad s divisibili per almeno una componente. Come abbiamo detto, esso ha s - x elementi, per cui l’equazione che cercavamo è:
Consideriamo il tratteggio T = (2, 3, 5) e sia x = 10. Come è possibile vedere, ad esempio, col visualizzatore di tratteggi, \mathrm{t\_spazio}_T(10) = 37: questo è il nostro s. Gli insiemi C(1), C(2), C(3) delle colonne divisibili rispettivamente per 2, 3 e 5, minori o uguali di 37 sono:
La cui unione, visualizzata in Figura 1, è
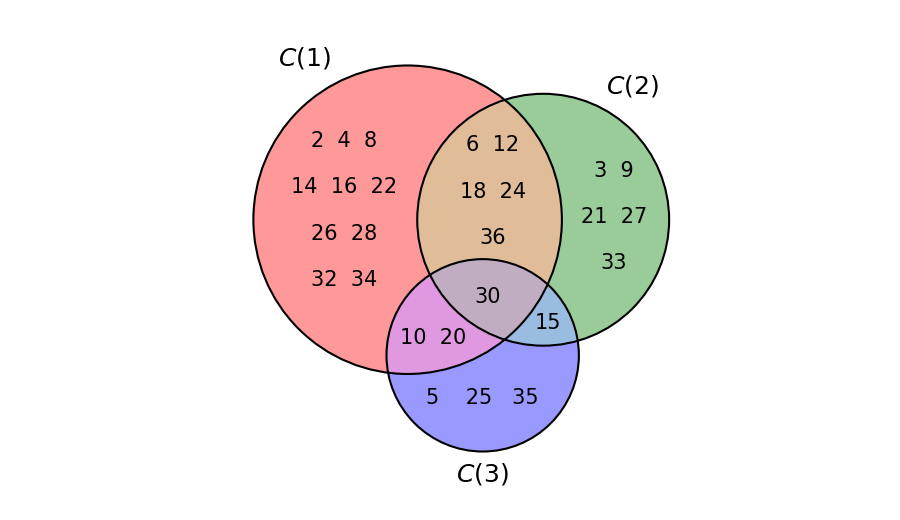
Abbiamo quindi che s - x = 37 - 10 = 27 = |C(1) \cup C(2) \cup C(3)|: per cui l’equazione (1), nel nostro caso, è verificata.
A questo punto entra in gioco il principio di inclusione-esclusione, che permette di calcolare, in generale, il numero di elementi dell’unione di più insiemi.
Il principio di inclusione-esclusione
Possiamo immaginare il principio di inclusione-esclusione, applicato agli insiemi C(1), \ldots, C(k), come un algoritmo di calcolo che procede in questo modo:
- Si inizializza un contatore m := 1. Si incrementerà questo contatore di un’unità alla volta, fino ad arrivare al numero di componenti k.
- Si elencano tutte le possibili combinazioni, senza ripetizione, di m indici scelti tra 1, \ldots, k:
- Se m = 1, le possibili combinazioni senza ripetizione di 1 indice sono gli indici stessi: 1, \ldots, k
- Se m = 2, le possibili combinazioni senza ripetizione di 2 indici sono (1, 2), (1, 3), (1, 4), \ldots, (1, k), (2, 3), (2, 4), \ldots, (2, k), (3, 4), \ldots, (3, k), \ldots, (k - 1, k)
- Se m = 3, le possibili combinazioni senza ripetizione di 3 indici sono (1, 2, 3), (1, 2, 4), \ldots, (1, 2, k), (1, 3, 4), (1, 3, 5), \ldots, (1, 3, k), \ldots, (1, k-1, k), (2, 3, 4), (2, 3, 5), \ldots, (k - 2, k - 1, k)
- …
- Per ciascuna combinazione di indici j_1, \ldots, j_m trovata al passo precedente, si conta il numero di elementi dell’intersezione degli insiemi C(j_1), \ldots, C(j_m):
- Se m = 1, stiamo considerando un solo insieme per volta e quindi non c’è nessuna intersezione da fare; vanno contati semplicemente gli elementi di ciascun insieme, |C(1)|, \ldots, |C(k)|
- Se m = 2, dobbiamo calcolare |C(1) \cap C(2)|, |C(1) \cap C(3)|, |C(1) \cap C(4)|, \ldots, |C(1) \cap C(k)|, |C(2) \cap C(3)|, |C(2) \cap C(4)|, \ldots, |C(2) \cap C(k)|, |C(3) \cap C(4)|, \ldots, |C(3) \cap C(k)|, \ldots, |C(k-1) \cap C(k)|
- Se m = 3, dobbiamo calcolare |C(1) \cap C(2) \cap C(3)|, |C(1) \cap C(2) \cap C(4)|, \ldots, |C(1) \cap C(2) \cap C(k)|, |C(1) \cap C(3) \cap C(4)|, |C(1) \cap C(3) \cap C(5)|, \ldots, |C(1) \cap C(3) \cap C(k)|, \ldots, |C(1) \cap C(k - 1) \cap C(k)|, |C(2) \cap C(3) \cap C(4)|, |C(2) \cap C(3) \cap C(5)|, \ldots, |C(k - 2) \cap C(k - 1) \cap C(k)|
- …
- Si sommano tutti i conteggi ottenuti al passo precedente, prendendoli col segno + se m è dispari, col segno – se m è pari:
- Se m = 1, la somma (con segno +) è |C(1)| + \ldots + |C(k)|
- Se m = 2, la somma è -(|C(1) \cap C(2)| + |C(1) \cap C(3)| + \ldots + |C(k-1) \cap C(k)|)
- Se m = 3, la somma è |C(1) \cap C(2) \cap C(3)| + |C(1) \cap C(2) \cap C(4)| + \ldots + |C(k - 2) \cap C(k - 1) \cap C(k)|
- …
- Se m \lt k, si incrementa m e si torna al passo 2. Se m = k si procede col passo successivo.
- Alla fine, si sommano tutti i risultati parziali ottenuti nel passo 4. ed il risultato è il numero di elementi di C(1) \cup \ldots \cup C(k).
Tutto ciò che abbiamo esposto in forma algoritmica si può esprimere in maniera compatta con la seguente formula, che costituisce l’enunciato del principio di inclusione-esclusione applicato agli insiemi C(1), \ldots, C(k):
La dimostrazione classica del principio di inclusione-esclusione è puramente tecnica, basata sul principio di induzione. A noi però non interessa tanto riportare questa dimostrazione, che è facile da trovare, quanto illustrare l’idea che sta alla base.
Ripartiamo dall’obiettivo iniziale, che era quello di contare le colonne contenenti almeno un trattino, ossia divisibili per almeno una delle componenti del tratteggio. Possiamo contare innanzitutto quelle divisibili per ciascuna componente del tratteggio. Contandole separatamente e sommando il tutto, alla fine abbiamo un totale di:
Abbiamo ottenuto così il primo termine della formula del principio di inclusione-esclusione. Il problema è che, se ci fermassimo qui, conteremmo due volte le colonne che sono divisibili per due componenti. Ad esempio, se una colonna è divisibile sia per n_1 che per n_2, nella formula (3) la contiamo una prima volta tra quelle divisibili per n_1 ed una seconda volta tra quelle divisibili per n_2, e la stessa cosa vale per le colonne divisibili per qualunque coppia di componenti n_i ed n_j (dove 1 \leq i \lt j \leq k). Dato che tutte queste colonne sono state contate due volte nella (3), possiamo tentare di correggere il nostro conteggio sottraendole dalla formula precedente:
Però anche così il conteggio non è ancora corretto. Infatti, se una colonna è divisibile per tre componenti del tratteggio (ammesso che esso abbia almeno tre componenti), essa nella formula (4) viene contata:
- Tre volte nella prima sommatoria, una volta per ciascuna componente per cui è divisibile
- Meno tre volte nella seconda sommatoria, una per ciascuna coppia di componenti per cui è divisibile. Infatti se una colonna è divisibile per tre componenti n_a, n_b ed n_c, essa è ovviamente divisibile per le stesse componenti prese a coppie, ossia per n_a ed n_b, per n_a ed n_c, e per n_b ed n_c, quindi rientra tre volte nella seconda sommatoria della (4), con (i, j) = (a, b), (i, j) = (a, c) e (i, j) = (b, c).
Quindi di fatto le colonne divisibili per tre componenti non sono contate affatto nella (4), perché esse danno al conteggio totale contributi uguali in valore assoluto, ma di segno opposto. Allora possiamo pensare di estendere la formula (4) aggiungendo proprio il numero di queste colonne:
Tuttavia, neanche questa formula può funzionare in generale, perché a questo punto, come si può immaginare, le colonne divisibili per quattro componenti (se ce ne sono) non sarebbero contate in modo corretto. Potremmo andare avanti, includendo un’ulteriore sommatoria il cui scopo è correggere il conteggio di queste colonne, e così via. Di certo, però, questo procedimento non può andare avanti all’infinito, perché le componenti del tratteggio sono k, che è un numero finito, e non ha senso chiedersi se esistono colonne divisibili per un numero di componenti maggiore di k. Questa è la ragione intuitiva per cui la formula con k sommatorie è quella corretta quando il numero di insiemi di partenza è k, esattamente come asserito dal principio di inclusione-esclusione.
Per k = 3, quindi considerando tre insiemi C(1), C(2) e C(3), abbiamo che:
- Per m = 1, dobbiamo contare, con segno positivo, il numero di elementi di ciascun insieme preso singolarmente
- Per m = 2, dobbiamo contare, con segno negativo, il numero di elementi di C(1) \cap C(2), C(1) \cap C(3) e C(2) \cap C(3)
- Per m = 3 = k, ultimo valore di m da considerare, dobbiamo contare, con segno positivo, il numero di elementi dell’unica intersezione possibile di tre insiemi, ossia C(1) \cap C(2) \cap C(3)
Per cui la formula (2) diventa:
Riprendendo l’esempio precedente, abbiamo che (v. Figura 1):
Per cui:
che è proprio il numero di elementi dell’unione C(1) \cup C(2) \cup C(3), come abbiamo verificato nell’esempio precedente.
Equazione caratteristica di \mathrm{t\_spazio} lineare di ordine generico
Tornando ai tratteggi, possiamo unire le formule (1) e (2), ottenendo:
Possiamo calcolare |C(i)|, |C(i) \cap C(j)|, |C(i) \cap C(j) \cap C(l)|, \ldots, |C(1) \cap \ldots \cap C(k)| applicando la Proposizione T.2 (Conteggio dei trattini fino a un certo valore in un tratteggio lineare di primo ordine), in modo del tutto simile a come abbiamo fatto per ottenere la Proposizione T.7 (Equazione caratteristica di \mathrm{t\_spazio} lineare di secondo ordine). Abbiamo così che
Sostituendo nella (6), abbiamo:
Abbiamo ottenuto così un’equazione in cui in linea di principio potremmo ricavare s, partendo dalla x che avevamo fissato a priori. Ragionando come per la Proposizione T.7, si può ottenere che questa equazione, unita al vincolo che le sue soluzioni siano spazi, caratterizza gli spazi del tratteggio, nel senso della seguente Proposizione:
Equazione caratteristica generale di \mathrm{t\_spazio} lineare
Sia T un tratteggio lineare di ordine k. Allora
La formula a destra del simbolo di equivalenza nella (9) è detta equazione caratteristica generale di \mathrm{t\_spazio} lineare.
Per k = 3, partendo dalla (9) otteniamo la seguente equazione caratteristica di \mathrm{t\_spazio} lineare di terzo ordine:
Ad esempio, nel caso del tratteggio T = (2, 3, 5) l’equazione diventa:
Per x = 10, e di conseguenza s = 37, ci ritroviamo coi conti dell’esempio precedente, in quanto:
Se nella (9) si ponesse k = 2, si riotterrebbe l’equazione caratteristica del secondo ordine, quella che compare nella Proposizione T.7. Volendo si potrebbe anche porre k = 1 ottenendo l’equazione caratteristica del primo ordine, quella della Proposizione T.3. Per questo nella Proposizione T.8 non abbiamo fatto ipotesi sull’ordine, includendo quindi anche il caso dei tratteggi di primo ordine. Tuttavia si tratta di un caso degenere che non mosterebbe il funzionamento del principio di inclusione-esclusione: perciò all’inizio abbiamo supposto che sia k \gt 1, anche se tecnicamente questo vincolo su k non è necessario.
Perché è così difficile risolvere l’equazione caratteristica generale
In linea di principio, risolvendo l’equazione (9) nell’incognita s si potrebbe calcolare \mathrm{t\_spazio} per tratteggi lineari di qualsiasi ordine. Vediamo perché questo è molto difficile.
La difficoltà di risolvere l’equazione (9) sta nel numero di parti intere che essa contiene. Nell’articolo su \mathrm{t\_spazio} di secondo ordine abbiamo visto che è già abbastanza difficile risolvere un’equazione simile con due parti intere (v. formula (8′) del Teorema T.12 (Soluzione dell’equazione caratteristica modificata di \mathrm{t\_spazio} lineare di secondo ordine)), infatti non abbiamo riportato la dimostrazione perché consiste di diverse pagine piene di calcoli. Abbiamo anche visto che è possibile risolvere un’equazione con tre parti intere grazie ad un piccolo artificio tecnico. Ma in generale, cosa possiamo aspettarci? Se, come sembra, la difficoltà di risolvere l’equazione crescesse col numero di parti intere, ci sarebbe da preoccuparsi, perchè il numero di parti intere dell’equazione (9), per l’ordine k, è esattamente 2^k - 1: la crescita del numero di parti intere dell’equazione caratteristica generale è esponenziale.
La causa di questa esplosione del numero di parti intere è il principio di inclusione-esclusione. Ripercorrendo il ragionamento che ci ha portato alla formula (9), si può osservare che vi è una parte intera per ogni possibile sottoinsieme non vuoto dei k indici 1, \ldots, k: dai sottoinsiemi di un solo elemento, che danno luogo alle parti intere \left \lfloor \frac{s}{n_1} \right \rfloor, \ldots, \left \lfloor \frac{s}{n_k} \right \rfloor, fino all’unico sottoinsieme di k elementi, ossia l’insieme di tutti gli indici, che dà luogo alla parte intera \left \lfloor \frac{s}{\mathrm{mcm}(n_1, \ldots, n_k)} \right \rfloor. Ma il numero di possibili sottoinsiemi di un insieme di k elementi è 2^k; escludendo l’insieme vuoto abbiamo la formula 2^k - 1, pertanto questo è anche il numero di parti intere nell’equazione (9).
Possiamo osservare questa crescita esponenziale già per k = 1, 2, 3:
- Per k = 1, 2^k - 1 = 2 - 1 = 1 parte intera: è quella che compare nella formula (4) della Proposizione T.3 (Equazione caratteristica di \mathrm{t\_spazio} lineare di primo ordine)
- Per k = 2, 2^k - 1 = 4 - 1 = 3 parti intere: sono quelle che compaiono nella formula (8) della Proposizione T.7 (Equazione caratteristica di \mathrm{t\_spazio} lineare di secondo ordine)
- Per k = 3, 2^k - 1 = 8 - 1 = 7 parti intere: sono quelle che compaiono nella formula (9′) di questo articolo
Insomma, se già è complicato risolvere l’equazione del secondo ordine, che ha solo tre parti intere, possiamo immaginare quanto sia complicato risolvere quella del terzo ordine, che ne ha 7, per non parlare degli ordini successivi, che ne hanno, nell’ordine, 15, 31, 63, 127, eccetera.
Fortunatamente in matematica spesso esistono più modi per risolvere lo stesso problema, ed in questo caso possiamo sperare che la risoluzione dell’equazione caratteristica generale non sia l’unica via per il calcolo di \mathrm{t\_spazio}.
Un importante punto aperto è trovare altri modi di ottenere una formula generale per \mathrm{t\_spazio}, senza risolvere esplicitamente l’equazione caratteristica.
Approssimazione di \mathrm{t\_spazio}
Un modo di rispondere al precedente punto aperto, aggirando parzialmente il problema, consiste nel non tentare di calcolare \mathrm{t\_spazio}, dato che è così difficile, ma di trovare una sua approssimazione. Idealmente, sarebbe un’ottima cosa stabilire una relazione, che valga per qualsiasi tratteggio lineare T, del tipo
dove f e \delta sono funzioni da determinare, e \delta è più piccola possibile. Naturalmente, si potrebbero anche scegliere delle funzioni \delta(x) diverse a destra e sinistra, ma ciò non cambierebbe la sostanza, per cui preferiamo la formulazione qui sopra, che, volendo, può essere abbreviata in
In realtà abbiamo già visto qualcosa di questo tipo. Ne abbiamo accennato parlando dei tratteggi di primo ordine, quando dopo il Teorema T.1 (Formula per il calcolo di \mathrm{t\_spazio} lineare di primo ordine) abbiamo osservato che, se dall’equazione caratteristica si toglie la parte intera (nel primo ordine ce n’è solo una), si ottiene un’equazione molto più semplice da risolvere, la cui soluzione s \approx \frac{n_1 x}{n_1 - 1} è molto simile a quella dell’equazione caratteristica, che è s = \left \lfloor \frac{n_1 x - 1}{n_1 - 1} \right \rfloor . In questo caso quindi la nostra f è data da f(x) = \frac{n_1 x}{n_1 - 1}. Per quanto riguarda \delta, una scelta possibile in questo caso è la funzione costante 1, in quanto
Questa relazione può essere dimostrata facilmente; a proposito, si potrebbe anche osservare che al posto dell’1 che compare a destra col ruolo di \delta(x), potrebbe esserci uno 0. Peccato però che sia una relazione di scarsa utilità, perché la funzione \mathrm{t\_spazio} di primo ordine è già così semplice che non ha bisogno di essere approssimata.
Possiamo fare un discorso analogo per il secondo ordine, supponendo per semplicità che le due componenti siano coprime, cioè che \mathrm{mcm}(n_1,n_2) = n_1 n_2. Con questo presupposto, se dalla formula (8) della Proposizione T.7 togliamo le parti intere, e di conseguenza sostituiamo il simbolo di uguaglianza con l’uguaglianza approssimata (\approx), essa diventa:
Questa equazione può essere risolta facilmente:
La frazione che moltiplica la x è interessante:
- Il numeratore è la lunghezza del periodo del tratteggio (ricordiamo che le componenti sono coprime)
- Il denominatore è il numero di spazi in un periodo (v. Proprietà T.7 (Calcolo del numero di spazi in un periodo di un tratteggio lineare di secondo ordine) e l’osservazione seguente)
Si può dimostrare che questo vale in generale: dato qualsiasi tratteggio lineare T, partendo dall’equazione caratteristica generale e togliendo da essa tutte le parti intere, si ottiene un’equazione molto semplice da risolvere, la cui soluzione è x che moltiplica la frazione
che per i tratteggi di secondo ordine, come nella (11), è
Questa frazione rappresenta la distanza costante che si avrebbe tra due spazi consecutivi di un tratteggio T, se essi fossero distribuiti uniformemente nel periodo (come accade ad esempio per i trattini su una riga). Stiamo dicendo quindi che la funzione \mathrm{t\_spazio} per un tratteggio lineare T sarebbe approssimabile come segue:
Quindi, con riferimento alla (10), la funzione x d_T avrebbe il ruolo della f, e \delta sarebbe da determinare. Gli spazi di un periodo di T sarebbero quindi all’incirca, nell’ordine, d_T, 2 d_T, 3 d_T, ..., \text{lunghezza di un periodo di } T (l’ultimo spazio si ottiene ponendo x = \text{numero di spazi in un periodo di } T nella formula (12)). Quindi d_T sarebbe non solo la distanza costante tra due spazi consecutivi, ma coinciderebbe anche col primo spazio.
Purtroppo tratteggi lineari siffatti non esistono. L’unico tratteggio lineare che ha spazi equidistanti tra loro è il tratteggio (2), per il quale d_T = \frac{2}{1} = 2, tuttavia d_T non coincide col primo spazio, che è 1:

Per tutti gli altri tratteggi lineari, gli spazi non sono distribuiti uniformemente, come si può facilmente notare in tutti gli altri esempi di tratteggi lineari fin qui presentati. Nonostante ciò, il modello di tratteggio con spazi distribuiti uniformemente sembra descrivere abbastanza bene i tratteggi lineari, dal punto di vista statistico. I dettagli li approfondiremo in un articolo dedicato, certamente però non basta fermarsi qui: bisogna cercare un’approssimazione di \mathrm{t\_spazio} che rappresenti un buon compromesso tra grado di approssimazione e semplicità delle funzioni f e \delta coinvolte. Questo resta un punto aperto.
Il campo d’indagine è quindi trovare due funzioni f e \delta tali che per ogni tratteggio lineare T:
La funzione \delta dovrebbe essere più piccola possibile, e al contempo le funzioni f e \delta non dovrebbero essere troppo complicate.