Prerequisiti:
- Il teorema di Chebyshev (versione debole)
- Il lemma dell’area dell’istogramma
- Dai numeri interi ai numeri reali
- Il fattoriale e la funzione Lambda*
- Il limite inferiore e il limite superiore di una successione
In questo articolo torneremo sul Teorema di Chebyshev, secondo cui la funzione \pi(x), che calcola il numero di numeri primi minori o uguali ad un intero positivo x, ha lo stesso ordine di grandezza di \frac{x}{\log x}. Vedremo che non solo le due funzioni hanno lo stesso ordine di grandezza, ma anche che, se esiste un limite per il loro rapporto, questo limite deve essere 1; in questo modo, avremo ottenuto una versione più “forte” del Teorema.
Ricordiamo che, per ottenere il Teorema di Chebyshev, abbiamo prima studiato le funzioni \theta(x) e \psi(x), stabilendo che sono asintoticamente equivalenti ed hanno ordine x (Teorema N.4). Analogamente, per ottenere la versione forte del Teorema, ci concentreremo su una di queste due funzioni, \psi(x).
La dimostrazione è interessante dal punto di vista tecnico, perché mette insieme diversi risultati precedenti:
- Si parte dalla connessione tra le funzioni \Lambda^{\star} e \psi^{\star} data dalla Proprietà N.6;
- Esprimendo questa connessione in forma logaritmica, possiamo applicarvi il lemma dell’area dell’istogramma;
- Il Teorema N.4 (Equivalenza asintotica e ordine di grandezza di \theta(x) e \psi(x)) e la Proposizione N.7 (Ordine di grandezza della funzione simil-fattoriale basata su \Lambda^{\star}) consentono di calcolare l’ordine di grandezza di due dei tre termini che compaiono nell’uguaglianza così ottenuta;
- Ragionando sul termine rimasto si ottengono informazioni sul limite superiore e sul limite inferiore della funzione \frac{\overline{\psi}(t)}{t}, estensione di \frac{\psi(x)}{x};
- Infine, ricordando l’equivalenza asintotica tra \pi(x) e \frac{\psi(x)}{\log x} (Corollario del Teorema N.5), si ottiene la versione forte del Teorema di Chebyshev.
Vediamo questi passaggi un po’ più nel dettaglio. Cominciamo dalla Proprietà N.6 (Connessione tra \Lambda^{\star} e \psi^{\star}):
Partendo da questa relazione, se ne può ottenere una più utile applicando il logaritmo ad ambo i membri:
dove la funzione \Lambda, secondo le nostre usuali notazioni, è definita come il logaritmo di \Lambda^{\star}:
Funzione \Lambda
Si definisce la funzione \Lambda: \mathbb{N}^{\star} \rightarrow \mathbb{R} tale che:
La funzione \Lambda è nota come funzione di von Mangoldt, in onore del matematico tedesco Hans von Mangoldt, che la definì per la prima volta. È possibile calcolarne il valore tramite il fattorizzatore.
Ad una lettura attenta, la (2) ricorda molto l’assunzione di base del lemma dell’area dell’istogramma, dove abbiamo n rettangoli aventi per base rispettivamente c_1, \ldots, c_n, ed abbiamo indicato con C_k la somma delle prime k basi, ossia C_k = \sum_{i = 1}^k c_i. Qui abbiamo simboli diversi: r al posto di i, x al posto di k, \Lambda(r) al posto di c_i e \psi(x) al posto di C_k, ma, fatte queste sostituzioni, la formula (2) è perfettamente sovrapponibile con la formula C_k = \sum_{i = 1}^k c_i che compare nell’enunciato del lemma. Possiamo quindi immaginare un istogramma di x rettangoli, dove l’r-esimo rettangolo, per r=1,\ldots,x, ha per base \Lambda(r), e la somma di tutte le basi è \psi(x). Relativamente a quella che nel Lemma è indicata con f, che è la funzione che rappresenta le altezze, possiamo scegliere quella che ci fa più comodo; in questo caso, per motivi che saranno chiari tra poco, poniamo che l’altezza dell’r-esimo rettangolo sia \frac{1}{r} (v. Figura 1):
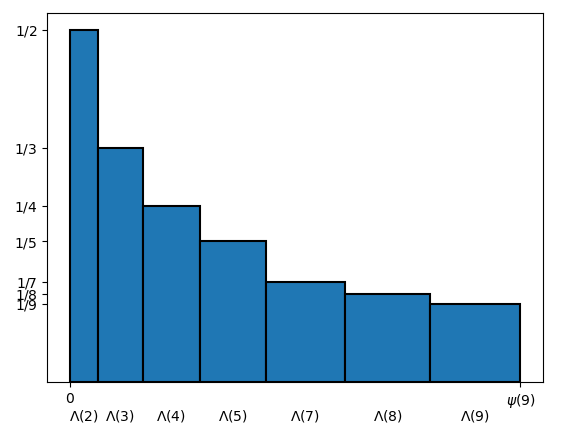
A questo punto, grazie alla seconda forma del lemma dell’area dell’istogramma, possiamo esprimere l’area dell’istogramma in due modi diversi, ottenendo la seguente uguaglianza:
Nel nostro caso, per applicare il Lemma N.5 (Lemma dell’area dell’istogramma, seconda forma), dobbiamo porre:
- n := x
- c_i := \Lambda(i)
- C(k) := \sum_{i = 1}^k \Lambda(i) = \psi(k)
- f(i) := \frac{1}{i}
- \widetilde{f}(t): [1, n + 1) \rightarrow \mathbb{R} \text{ tale che } \widetilde{f}(t) := \frac{1}{t} (estensione di f)
Con queste scelte, si ottiene:
Che è identica alla (3), salvo il nome della variabile della sommatoria.
L’integrale che compare nella formula (3) potrebbe avere come estremo inferiore 2 invece di 1. Infatti \psi(1) = \Lambda(1) = 0, per cui l’estensione semplice \overline{\psi} è sempre nulla nell’intervallo [1, 2), annullando così l’integrale in questo intervallo.
Per quanto riguarda il termine \frac{\psi(x)}{x}, ne conosciamo già l’ordine asintotico. Infatti, per il Teorema N.4 (Equivalenza asintotica e ordine di grandezza di \theta(x) e \psi(x)), la funzione \psi(x) ha ordine x e dunque \frac{\psi(x)}{x} ha ordine 1, cioè, per la Proprietà A.7, è una funzione definitivamente limitata. Quindi possiamo riscrivere la (3) come segue:
Il motivo per cui abbiamo scelto come altezza dei rettangoli \frac{1}{r} è proprio per far comparire il termine \frac{\psi(x)}{x}, che abbiamo semplificato facilmente grazie al Teorema N.4.
Per quanto riguarda il primo termine, possiamo calcolarne l’ordine di grandezza attraverso le proprietà della funzione \Lambda^{\star} e la sua relazione con la funzione fattoriale, di cui abbiamo parlato nell’articolo 13. Il fattoriale e la funzione Lambda*. In particolare, questo termine si ottiene dal seguente corollario della Proposizione N.7 (Ordine di grandezza della funzione simil-fattoriale basata su \Lambda^{\star}):
Ordine di grandezza della funzione simil-fattoriale basata su \Lambda^{\star}, versione logaritmica
Applicando il logaritmo ad ambo i membri della Proposizione N.7, si ottiene:
Da cui, dividendo tutto per un fattore x, si ottiene l’enunciato del Corollario. In quest’ultimo passaggio si applica la Proprietà A.8A, per la quale \frac{O(x)}{x} = \frac{x \cdot O(1)}{x} = O(1).
Sostituendo nella (4), abbiamo:
da cui, utilizzando le proprietà degli ordini asintotici Corollario 3 della Proprietà A.8 e Corollario della Proprietà A.9, si ottiene:
Questa equazione può darci informazioni sulla funzione \frac{\overline{\psi}(t)}{t}, che possiamo mettere in evidenza all’interno dell’integrale:
La questione può essere espressa in modo più generale con la seguente domanda: se una funzione f: [1, +\infty) \rightarrow \mathbb{R} soddisfa l’equazione
cosa possiamo dire su f?
Innanzitutto, se nella (5) sostituiamo f = 1 (la funzione costante di valore 1) abbiamo che
Quindi scegliendo f = 1 i conti tornano. Ma non è detto che f debba essere sempre costante di valore 1. Intuitivamente, dato che l’operazione di integrale calcola l’area compresa tra il grafico di f e l’asse orizzontale, f potrebbe oscillare un po’ sopra e un po’ sotto il valore 1, in modo tale però che l’area delle parti dove è sopra 1 compensino quelle dove è sotto, e l’area totale sia comunque pari a \log x più una quantità definitivamente limitata. L’importante è che le parti di area in cui la funzione è maggiore di 1 non siano “troppo grandi” rispetto a quelle dove la funzione è minore di 1: deve esserci un certo equilibrio.
Per tradurre in termini più formali questa intuizione, possiamo far ricorso ai concetti di limite superiore e di limite inferiore, che abbiamo visto nel precedente articolo. Si può dimostrare infatti che, se f soddisfa la (5), deve valere la seguente coppia di disuguaglianze:
Qui il limite superiore ed il limite inferiore sono applicati ad una funzione, mentre nel precedente articolo li abbiamo sempre applicati a successioni; tuttavia le definizioni sono molto simili nei due casi. Ad esempio la Definizione A.7, secondo la quale qualunque intervallo più grande di [\lim \inf f_n, \lim \sup\ f_n] contiene quasi tutti i termini di una successione (f_n), resta praticamente identica se al posto della successione (f_n) si considera una funzione f(t). Ciò che cambia è solo la definizione di “quasi tutti i termini”, che nel caso delle successioni significa tutti tranne al più un numero finito; nel caso delle funzioni è un concetto leggermente più complesso, ma molto simile, che per brevità non tratteremo per il momento.
Nel nostro caso f(t) = \frac{\overline{\psi}(t)}{t}, quindi la (6) si riscrive come:
In realtà, tornando ai numeri interi, si può dimostrare che le stesse relazioni continuano a valere se si considera la funzione \psi: \mathbb{N}^{\star} \rightarrow \mathbb{N} al posto della sua estensione semplice \overline{\psi}: \mathbb{R}^{\star} \rightarrow \mathbb{N}:
Questo però è un passaggio delicato su cui ci soffermeremo nei prossimi articoli. Per il momento ci accontentiamo del risultato parziale dato dalla (6′):
Limite inferiore e limite superiore della funzione \frac{\overline{\psi}(t)}{t}
Consideriamo l’equazione (5) e supponiamo che sia \lim \inf f \gt 1. Se al posto di f avessimo una successione f_n, in base alla Definizione A.7 potremmo concludere che qualsiasi intervallo più grande di [\lim \inf f_n, \lim \sup f_n] contiene quasi tutti i termini della successione. Ma se \lim \inf f_n \gt 1, vuol dire che quasi tutti i termini della successione sono maggiori di 1. Infatti, se poniamo \delta := \lim \inf f_n - 1, in modo che sia \lim \inf f_n = 1 + \delta, allora l’intervallo [1 + \frac{\delta}{2}, \lim \sup f_n] è un intervallo più grande di [\lim \inf f_n, \lim \sup f_n], contenente perciò quasi tutti i termini della successione. Allora quasi tutti i termini della successione sono maggiori o uguali di 1 + \frac{\delta}{2}, quindi maggiori di 1. Ma se quasi tutti i termini sono maggiori di 1, vuol dire che il numero di quelli minori o uguali di 1 è finito (questa terminologia è stata introdotta nell’articolo precedente). Allora esisterà certamente un indice N tale che f_N è l’ultimo termine della successione minore o uguale ad 1; equivalentemente, possiamo dire che per ogni n \gt N, tutti i termini della successione sono maggiori di 1.
Tornando alla funzione f, anche se non abbiamo visto la definizione di limite superiore e di limite inferiore per le funzioni, possiamo immaginare che, attraverso un ragionamento simile, si arrivi ad una analoga conclusione: se fosse \lim \inf f \gt 1, esisterebbe un numero reale T tale che, per ogni t \gt T, f(t) \gt 1.
Torniamo ora all’equazione (5). Si tratta di un’equazione funzionale: essa dice che l’integrale \int_1^x f(t) \frac{1}{t} dt, visto come funzione in x, è pari alla funzione \log x più una funzione definitivamente limitata. La domanda è: questa equazione rimane valida se supponiamo l’esistenza di questo T?
Trattandosi di una relazione asintotica, dobbiamo vedere cosa succede quando x tende ad infinito. Immaginiamo quindi di calcolare l’integrale \int_1^x f(t) \frac{1}{t} dt, partendo da x = 1, per valori crescenti di x. Inizialmente x sarà sempre minore o uguale di T: il primo valore maggiore di T sarà x = \left \lfloor T \right \rfloor + 1. A quel punto avremo ottenuto un certo valore per l’integrale
ma questo valore non ci interessa: lo indicheremo con una costante A. È più interessante invece cosa succede continuando ad incrementare la x. In tal caso potremo spezzare l’integrale in due parti, come segue:
In questo nuovo integrale, la funzione f è sempre maggiore di 1, perché t \geq \left \lfloor T \right \rfloor + 1 \gt T. Essendo f maggiore di 1, possiamo dire equivalentemente che f \geq 1 + \epsilon per qualche costante \epsilon \gt 0. Dunque possiamo continuare le precedenti uguaglianze come segue:
Da cui, raggruppando tutte le costanti presenti in un’unica costante B, si ottiene:
Se fosse vera la (5), dovrebbe essere B + \epsilon x = O(1), cioè la funzione B + \epsilon x dovrebbe essere definitivamente limitata. Ma questo non è vero, perché al crescere di x si otterrebbero valori sempre più grandi di questa funzione, essendo \epsilon \gt 0. Avendo ottenuto questa contraddizione, significa che la nostra assunzione di partenza, \lim \inf f \gt 1, è falsa: quindi, se è vera la (5), deve essere \lim \inf f \leq 1.
Per quanto riguarda il limite superiore, si può ragionare in modo analogo partendo dall’assunzione che \lim \sup f \lt 1. Si concluderà che, se è vera la (5), tale ipotesi deve essere falsa, cioè deve essere \lim \sup f \geq 1.
Infine, sostituendo f(t) = \frac{\overline{\psi}(t)}{t}, come si è detto, si ottiene la formula (6′).
Possiamo riscrivere l’enunciato del Teorema N.7 come segue:
Ora possiamo utilizzare l’equivalenza asintotica tra \pi(x) e \frac{\psi(x)}{\log x} (Teorema N.5). Modificando opportunamente la dimostrazione di questo teorema (cosa che per brevità non faremo), si può dimostrare che non solo queste funzioni sono asintoticamente equivalenti, ma che lo sono anche le loro estensioni \overline{\pi}(t) e \frac{\overline{\psi}(t)}{\log t}. Quindi, nel calcolo sia del limite inferiore che di quello superiore, possiamo sostituire \frac{\overline{\psi}(t)}{\log t} con \overline{\pi}(t), ottenendo:
Riscrivendo quest’equazione in una forma leggermente diversa, si ottiene il seguente Corollario:
Limite superiore e limite inferiore della funzione \overline{\pi}(t) / \frac{t}{\log t}
Il Corollario è visualizzato graficamente in Figura 2, dove per semplicità sono rappresentati i valori della funzione \overline{\pi}(t) / \frac{t}{\log t} soltanto in corrispondenza della variabile intera x \in \mathbb{N}^{\star}.
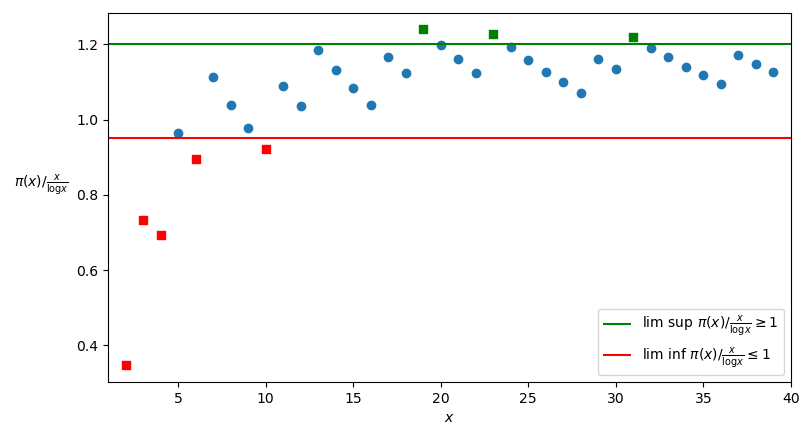
Se applichiamo all’enunciato del Corollario la Proprietà A.3 (Una successione reale ammette limite se e solo se il suo \lim \inf e il suo \lim \sup coincidono), ne otteniamo infatti la seguente versione alternativa, che è quella che chiameremo “versione forte” del Teorema di Chebyshev (per altri autori, semplicemente “Teorema di Chebyshev”):
Teorema di Chebyshev: versione forte
Se la funzione \pi(x) / \frac{x}{\log x} tende a un limite, questo limite è 1.
Supponiamo che la funzione \overline{\pi}(t) / \frac{t}{\log t} tenda ad un limite l. Per la Proprietà A.3 (Una successione reale ammette limite se e solo se il suo \lim \inf e il suo \lim \sup coincidono), che si dimostra anche per le funzioni, deve essere allora
Ma se \lim \inf \overline{\pi}(t) / \frac{t}{\log t} e \lim \sup \overline{\pi}(t) / \frac{t}{\log t} sono uguali, per il Corollario del Teorema N.7 non possono che essere entrambi 1, quindi, per la (7), l = 1 e quindi \lim_{t \to +\infty} \overline{\pi}(t) / \frac{t}{\log t} = 1.
Infine, se \lim_{t \to +\infty} \overline{\pi}(t) / \frac{t}{\log t} = 1, anche \lim_{x \to \infty} \pi(x) / \frac{x}{\log x} = 1, perché quest’ultima funzione (o meglio successione) è una restrizione su \mathbb{N}^{\star} della prima (in generale, se \lim_{t \to +\infty} f(t) = l, anche \lim_{n \to +\infty} f(a_n) = l, per qualunque successione a_n che tende a +\infty).
La versione forte del Teorema di Chebyshev sembra essere smentita dal grafico mostrato in Figura 2, nel quale sembra che i valori della funzione \pi(x) / \frac{x}{\log x} tendano ad essere maggiori di 1. In realtà, se si prolungasse il grafico, si vedrebbe che i valori della funzione tendono effettivamente ad 1, decrescendo però in modo estremamente lento. Per avere un’idea di quanto sia lenta questa decrescita, basta osservare il grafico della funzione per x \leq 100.000.000 (Figura 3):
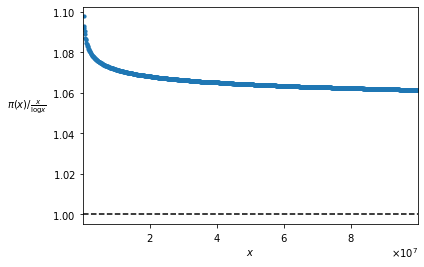
La funzione sembra non arrivare mai a 1; eppure, abbiamo appena dimostrato che, se esiste un limite, questo limite è 1. Questo è uno dei casi in cui la teoria fa vedere cose che in pratica sono difficili da vedere, almeno negli ordini numerici che siamo abituati a trattare.
Per capire perché questo Corollario sia chiamato “versione forte” del Teorema di Chebyshev, ricordiamo la precedente versione (“debole”) del Teorema (Corollario II del Teorema N.5):
In base a questa relazione asintotica, per la Definizione A.4 (Relazioni asintotiche, definizioni alternative utilizzando i limiti), se esistesse il limite del rapporto \pi(x) / \frac{x}{\log x}, esso potrebbe essere una qualunque costante reale non nulla. In tal senso, la versione “forte” è chiamata così perché vincola questa costante in modo molto più stringente, dicendo che deve essere 1.