Prerequisiti:
- Elementi di analisi asintotica
- Il Teorema di Chebyshev: versione debole
- Il lemma dell’area dell’istogramma
- Dai numeri interi ai numeri reali
- La somma degli inversi dei primi numeri interi positivi
- Il limite inferiore e il limite superiore di una successione
- Proprietà degli ordini asintotici
- Il Teorema di Chebyshev: versione forte
- Le funzioni W e V
- La media integrale e la funzione di errore assoluto R
- Il Teorema di Selberg: dimostrazione e applicazione
Guardando all’indietro il percorso fatto finora, possiamo individuare un punto di svolta: è stato quando abbiamo introdotto l’Ipotesi N.1, che consiste in una disuguaglianza in cui è presente un integrale. A quel punto, per semplificare, abbiamo deciso di sostituire l’integrale con una sommatoria (operazione ragionevole, perché l’integrale secondo Riemann è definito come il limite di una sommatoria) e da allora abbiamo lavorato sempre con le sommatorie, fino a dimostrare il Teorema di Selberg e alcune sue conseguenze. Abbiamo ottenuto così delle relazioni simili all’Ipotesi N.1, se non fosse per la presenza delle sommatorie al posto degli integrali. Ora è giunto il momento di ritornare alla forma integrale, per riallacciarci al discorso che ci ha condotto all’Ipotesi N.1, tentando di dimostrarla.
Ricordiamo che l’Ipotesi N.1 consiste nel supporre che la relazione \alpha \leq \beta (dove le costanti \alpha e \beta sono state introdotte con la Definizione N.14) valga senza il limite superiore, ossia che per ogni intero positivo x valga l’ipotetica relazione:
La relazione più simile a cui siamo arrivati finora, nell’articolo precedente, è quella del Corollario 2 della Proposizione N.8:
dove gli a_n sono tali che:
L’obiettivo che ci poniamo in questo articolo è passare dalla relazione (2) ad una relazione del tipo:
Vogliamo cioè passare da una sommatoria con coefficienti a_n ad un integrale con termini f(t) da determinare.
Il primo problema, in questo procedimento, è stabilire quale ordine asintotico ci serve nella formula (3): in questo modo potremo capire qual è la funzione f più opportuna.
Determinazione dell’ordine asintotico da utilizzare nel passaggio all’integrale: una possibile dimostrazione alternativa
Per capire quale ordine asintotico ci serve nella (3), consideriamo per il momento cosa succederebbe col logaritmo senza il quadrato. Nell’articolo precedente, in particolare nella Figura 2, abbiamo visto che empiricamente risulta verosimile la seguente relazione asintotica:
Rimanendo sempre a livello empirico, nell’articolo precedente abbiamo visto che la sommatoria \sum_{n \leq x} \Lambda(n) \left|R\left(\frac{x}{n}\right)\right| è ben approssimata dall’integrale \int_1^x \left| R\left(\frac{x}{t}\right) \right| dt, per cui risulterebbe:
Se si dimostrasse che questo piccolo errore che si osserva sperimentalmente fosse un O(x), per il Corollario della Proprietà A.9 i due termini più a destra si unirebbero in un unico termine O(x) + O(x) = O(x):
per cui l’Ipotesi N.1 sarebbe dimostrata a meno di un termine di ordine O(x). Questa formula sembra coerente coi dati effettivi, come mostra il grafico seguente, dove O(x) sembra essere poco più piccolo in valore assoluto della funzione -\frac{3}{2} x:
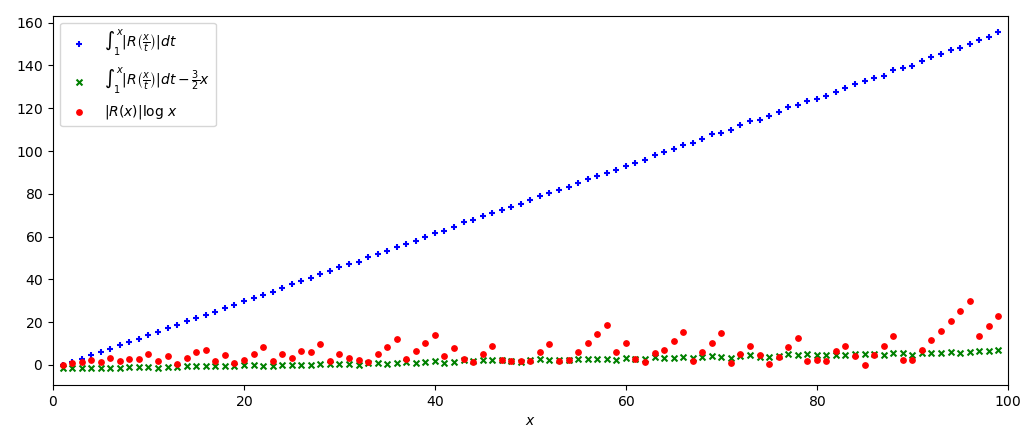
A questo punto riteniamo utile fare una breve digressione: vediamo quali implicazioni avrebbe la (5′), se fosse dimostrata. Per fare ciò, esprimiamola in termini della funzione V. Utilizzando la formula (13) dell’articolo La media integrale e la funzione di errore assoluto R, dalla (5′) si ottiene:
da cui, dividendo tutto per x, applicando la Proprietà A.8A e ricordando che, per la formula (12) dell’articolo citato, V(\log x) = \frac{R(x)}{x}:
Dividendo tutto per \log x e applicando nuovamente la Proprietà A.8A si ottiene:
da cui, prendendo il limite superiore di ambo i membri ed osservando che il limite superiore di un O(\frac{1}{\log x}) è zero, si ottiene:
Perché il limite superiore di un O(\frac{1}{\log x}) è zero?
L’espressione “il limite superiore di un O(\frac{1}{\log x}) è zero” significa che, considerata una qualunque funzione f = O(\frac{1}{\log x}), si ha che \limsup_{x \to +\infty} f(x) = 0. Vediamo perché. Se f = O(\frac{1}{\log x}) allora, per la Definizione A.4, \lim_{x \to +\infty} f(x) / \frac{1}{\log x} = L, dove L \in \mathbb{R}. Allora \lim_{x \to +\infty} f(x) \log x = L, e in particolare, per la Proprietà A.3, \limsup_{x \to +\infty} f(x) \log x = L. Ma \limsup_{x \to +\infty} \log x = \lim_{x \to +\infty} \log x = +\infty, dunque l’unica possibilità per cui si abbia \limsup_{x \to +\infty} f(x) \log x = L è che il limite superiore di f(x) sia 0, perché se fosse \pm \infty o un altro numero reale, il limite superiore del prodotto f(x) \log x sarebbe \pm \infty (abbiamo assunto che per il limite superiore di un prodotto valgano proprietà analoghe a quelle del limite). Quindi \limsup_{x \to +\infty} f(x) = 0.
Ricordando la Definizione N.14 (Costanti \alpha e \beta), la (6) può essere scritta semplicemente come:
Ma questa è proprio la relazione che volevamo dimostrare! Quindi, se la formula (5′) fosse dimostrata, essa consentirebbe di semplificare considerevolmente una parte della dimostrazione del Teorema dei numeri primi: perciò riteniamo che sia importante. Vedremo infatti, in questo articolo e nel prossimo, che la dimostrazione canonica della formula (6′) richiede degli artifici tecnici abbastanza pesanti.
A questo punto molti nostri lettori potranno chiedersi: perché non vale la pena completare questa dimostrazione alternativa, se promette di essere più semplice? In realtà non lo sappiamo, per cui per noi l’unico modo per rispondere a questa domanda sarebbe quello di provare. Potrebbe emergere qualche grossa difficoltà tecnica, e questo potrebbe essere il motivo per cui Erdős e Selberg hanno preferito seguire un’altra strada, apparentemente più complessa. O magari, chissà, si potrebbe riuscire nello scopo, ottenendo effettivamente una dimostrazione più semplice del fatto che \alpha \leq \beta… questa può essere una bella sfida per i nostri lettori!
Ora torniamo alla dimostrazione vera e propria. Per ottenere lo stesso membro di sinistra della (3), moltiplichiamo ambo i membri della (5′) per \log x (utilizzando anche il Corollario 1 della Proprietà A.8):
Se confrontiamo questa formula con la (3), possiamo dire che l’ordine asintotico che cerchiamo dovrebbe essere O(x \log x). Naturalmente questa non è una dimostrazione, perché si basa sulla formula (5′) che non abbiamo dimostrato, ma dà l’idea di cosa cercare, e nel prossimo paragrafo dimostreremo che quest’idea è corretta.
L’Ipotesi N.1 per noi resterà purtroppo un problema aperto. Ci serviva come spunto di partenza per sviluppare la dimostrazione, ma per proseguire non è essenziale dimostrare se essa sia vera o falsa, per cui non lo faremo. Noi riteniamo che essa sia vera a meno di un termine O(x), ossia che valga la formula (5′); perciò l’Ipotesi N.1 si riallaccia al discorso fatto finora.
Strategia della dimostrazione: le due fasi
Supponiamo l’idea sviluppata nel paragrafo precedente sia corretta, cioè che l’ordine asintotico che compare nella (3) sia proprio O(x \log x):
Una tecnica per dimostrare questa relazione è utilizzare una sommatoria come passaggio intermedio verso l’integrale, ossia dimostrare che:
dove la prima disuguaglianza è la formula (2) che abbiamo visto all’inizio, mentre la seconda, per le proprietà degli ordini asintotici Corollario 3 della Proprietà A.8, Proprietà A.10 e Corollario della Proprietà A.9, è equivalente a:
Quindi dobbiamo dimostrare quest’ultima relazione asintotica. Lo faremo in due fasi, introducendo un’espressione che è un po’ una via di mezzo tra la sommatoria e l’integrale:
- La prima fase consiste nel dimostrare che:
\left| \sum_{n \leq x} a_n \left|R\left(\frac{x}{n}\right)\right| - \sum_{2 \leq n \leq x} \left|R\left(\frac{x}{n}\right)\right| \int_{n-1}^n f(t) dt \right| = O(x \log x) \tag{8}
- La seconda fase consiste nel dimostrare che:
\left| \sum_{2 \leq n \leq x} \left|R\left(\frac{x}{n}\right)\right| \int_{n-1}^n f(t) dt - \int_1^x f(t) \left| R\left(\frac{x}{t}\right) \right| dt \right| = O(x \log x) \tag{9}
Ora chiamiamo A := \sum_{n \leq x} a_n \left|R\left(\frac{x}{n}\right)\right|, B := \sum_{2 \leq n \leq x} \left|R\left(\frac{x}{n}\right)\right| \int_{n-1}^n f(t) dt e C := \int_1^x f(t) \left| R\left(\frac{x}{t}\right) \right| dt, per cui il valore assoluto della (8) diventa |A - B| e quello della (9) diventa |B - C|. Così, mettendo insieme i risultati delle due fasi, si ottiene:
da cui, per la Proprietà A.12, A - C = O(x \log x), che è la (7).
Le due fasi della dimostrazione sono una la conseguenza dell’altra, nel senso che la funzione f(t) si può determinare dalla (8), cioè completando la prima fase; successivamente, nella seconda fase, si verifica che la funzione trovata soddisfa anche la (9).
Con diversi passaggi tecnici, si dimostra che la funzione cercata è f(t) = 2 \log t. Quindi, ripercorrendo i passaggi a ritroso, si può sostituire questa funzione anche nella (3′), ottenendo:
Conseguenza del Teorema di Selberg, forma integrale
Per prima cosa osserviamo che, nella (8), il coefficiente a_1 è peri a zero. Infatti dobbiamo ricordare che i coefficienti che abbiamo indicato con a_n sono stati ottenuti dal Corollario 1 della Proposizione N.8 (Conseguenza del Teorema di Selberg), ponendo:
Ma, se n = 1, si ha che a_1 = \Lambda(1) \Lambda(1) + \Lambda(1) \log 1, per cui, essendo \Lambda(1) = \log 1 = 0 (per la Definizione N.11), si ha che a_1 = 0. Quindi nella (8) possiamo sostituire la sommatoria \sum_{n \leq x} a_n \left|R\left(\frac{x}{n}\right)\right| con la sommatoria \sum_{2 \leq n \leq x} a_n \left|R\left(\frac{x}{n}\right)\right|, che si può combinare con la successiva come segue:
Ponendo c_n := a_n - \int_{n-1}^n f(t) dt, quest’ultima formula si può riscrivere come segue:
Applicando il Lemma dell’area dell’istogramma, si ottiene quindi:
dove, per ogni n = 2, \ldots, x:
Quest’espressione è importante perché introduce la sommatoria \sum_{h \leq n} a_h, che conosciamo per la (2′).
Osserviamo che \left|R\left(\frac{x}{x}\right)\right| = R(1) = \overline{\psi}(1) - 1 = \psi(1) - 1 = \log \psi^{\star}(1) = \log 1 = 0 (abbiamo applicato le Definizioni N.15, N.8, N.7 e N.5), per cui il primo termine dentro il valore assoluto della (a) va via:
Per la disuguaglianza triangolare:
Quindi, per dimostrare la (a’), che a sua volta è equivalente alle formule precedenti, per la Proprietà A.12 ed il Corollario della Prorietà A.6 bisogna dimostrare che:
A questo punto, per trovare la funzione f(t), dobbiamo prima “indovinare” l’ordine asintotico di C(n), in modo tale che sia soddisfatta quest’ultima relazione asintotica. Fatto ciò, potremo sostituire l’ordine asintotico nella (b) e così finalmente capire qual è la funzione f(t).
Ora troviamo una maggiorazione per l’espressione \left| \left|R\left(\frac{x}{n}\right)\right| - \left|R\left(\frac{x}{n+1}\right)\right| \right|. Per trovarla possiamo usare una proprietà generale delle disuguaglianze col valore assoluto: se k e h sono due numeri reali, si ha che \left| |k| - |h| \right| \leq |k - h|. Questa proprietà è una conseguenza della disuguaglianza triangolare; infatti per questa disuguaglianza, se a e b sono due numeri reali, si ha che |a + b| \leq |a| + |b|, da cui |a + b| - |a| \leq |b| e, applicando il valore assoluto ad ambo i membri, \left||a + b| - |a|\right| \leq |b|. Se in quest’ultima disuguaglianza poniamo a := h e b := k - h, otteniamo che \left||k| - |h|\right| \leq |k - h|, che è la proprietà che abbiamo menzionato. Applicandola, abbiamo che:
Utilizzando la Definizione N.15 e alcuni semplici passaggi algebrici, otteniamo:
dove nell’ultimo passaggio si è osservato che \frac{x}{n} \gt \frac{x}{n + 1} e \overline{\psi}\left(\frac{x}{n}\right) \geq \overline{\psi}\left(\frac{x}{n+1}\right), essendo \overline{\psi} una funzione crescente (in quanto estensione semplice della funzione \psi = \log \psi^{\star}, dove \psi^{\star} è crescente per definizione).
Unendo la (d) e la (e), abbiamo:
per cui, sostituendo nella (c):
Ora, in assenza di vincoli particolari, una scelta ovvia per C(n) sarebbe C(n) := 1 perché in questo modo la sommatoria, unita all’alternanza dei segni, farebbe sì che la maggior parte dei termini si semplifichino a vicenda. Per i nostri scopi però è più conveniente un’altra scelta, leggermente più complessa ma che produce un effetto di semplificazione simile: C(n) := n. Con questa scelta abbiamo:
dove:
- nel passaggio (*) abbiamo applicato il Teorema N.4, secondo il quale \psi(x) \asymp x, per cui \psi(x) = O(x) e quindi anche \overline{\psi}(x) = O(x) (infatti \overline{\psi} e \psi per definizione di estensione semplice differiscono al massimo di un’unità, quindi di un O(1), per cui \overline{\psi}(x) = \psi(x) + O(1) = O(x) + O(1) = O(x));
- nel passaggio successivo abbiamo applicato la Proprietà A.8A e il Teorema N.6 (per quest’ultimo, \sum_{1 \leq n \leq x} \frac{1}{n} = \log x + \gamma + O\left(\frac{1}{x}\right), ma \gamma e O\left(\frac{1}{x}\right) sono entrambi O(1) rispettivamente per il Corollario della Proprietà A.7 e la Proprietà A.10);
- nel passaggio seguente abbiamo applicato la Proprietà A.9 per portare il sibolo di O grande fuori dalla sommatoria; abbiamo anche osservato che 1 + \frac{1}{2} + \frac{1}{x} è una costante e quindi è O(1) per il Corollario della Proprietà A.7;
- nei passaggi seguenti abbiamo osservato che possiamo applicare alla sommatoria \sum_{2 \leq n \leq x - 1} \frac{1}{n} lo stesso ragionamento già fatto per la sommatoria \sum_{3 \leq n \leq x - 1} \frac{1}{n}; inoltre abbiamo applicato le proprietà degli ordini asintotici Corollario 1 della Proprietà A.8, Proprietà A.5 e Proprietà A.10.
Osserviamo che, se nella formula iniziale della (g) mettiamo O(n) al posto di n, il risultato finale non cambia:
dove nella prima, nella seconda e nell’ultima uguaglianza abbiamo usato rispettivamente le proprietà Corollario 1 della Proprietà A.8, Proprietà A.9 e Proprietà A.11.
Ma se C(n) = O(n), anche |C(n)| = O(n), per il Corollario della Proprietà A.6). Quindi, per la (f) e la (h):
Ma allora, per la Proprietà A.12:
quindi abbiamo dimostrato la (c), che era il nostro obiettivo intermedio. Ciò significa che la scelta C(n) := O(n) è plausibile dal punto di vista degli ordini asintotici. Resta da determinare qual è la funzione f, in base alla (b). Se infatti nella (b) sostituiamo C(n) := O(n), otteniamo:
Le possibili funzioni f a questo punto si possono ottenere derivando ambo i mebri rispetto ad n. A tal proposito osserviamo due cose: per prima cosa n è un intero, quindi per effettuare il passaggio di derivazione bisognerebbe sostituirlo con una variabile reale; inoltre la soluzione non è univoca perché ad esempio, se f è una soluzione, anche f + c è una soluzione per ogni costante c. Per brevità preferiamo saltare i passaggi e verificare direttamente che la funzione f(t) := 2 \log t è una possibile soluzione (di fatto è la soluzione più semplice possibile):
dove nel secondo passaggio abbiamo applicato l’integrale del logaritmo, che si svolge per parti ed è spesso utilizzato come esercizio nei corsi di analisi.
Ricapitolando, possiamo dire che:
- La funzione f(t) := 2 \log t soddisfa la (b), facendo in modo che C(n) = O(n)
- Se C(n) = O(n) risulta soddisfatta la (c), quindi anche la (a’), che a sua volta è equivalente alla (8)
- Quindi la funzione f(t) := 2 \log t soddisfa la (8)
Per dimostrare la (9), per prima cosa sostituiamo al posto di f la funzione f(t) := 2 \log t che abbiamo trovato nella dimostrazione della (8):
Il membro di sinistra si può sviluppare come segue:
dove nel passaggio (*) abbiamo applicato una disuguaglianza che si dimostra con fomule analoghe alle (d) ed (e) del dettaglio precedente:
dove nell’ultimo passaggio abbiamo considerato che t \leq n, essendo la variabile di integrazione di un integrale tra n - 1 ed n. Per lo stesso motivo si ha anche che t \geq n - 1, relazione che è stata usata nella (i) nel passaggio (**) per ottenere un’espressione che, non dipendendo da t, può essere portata fuori dall’integrale. Nella (i) resta quindi da sviluppare l’integrale \int_{n-1}^n 2 \log t\ dt (come nel dettaglio precedente, supponiamo che sia noto l’integrale indefinito del logaritmo):
Osserviamo che (n - 1) \log \frac{n}{n-1} = \log \left( \frac{n}{n-1} \right) ^ {n - 1} = \log \left( 1 + \frac{1}{n-1} \right) ^ {n - 1} e, per un limite notevole, l’espressione \left( 1 + \frac{1}{n-1} \right) ^ {n - 1}, per n \to \infty, tende al numero di Nepero e. Quindi, per n \to \infty, (n - 1) \log \frac{n}{n-1} \to \log e = 1, per cui a livello di ordine asintotico è esprimibile come O(1) (questa è una conseguenza della Proprietà A.7). Tenendo conto che, come noto in analisi, \log n = o(n), e quindi per la Proprietà A.10 \log n = O(n), abbiamo che:
dove abbiamo applicato la Proprietà A.10, il Corollario della Proprietà A.9 e il Corollario 2 della Proprietà A.8.
Unendo la (j) e la (k) abbiamo:
Sostituendo nella (i) abbiamo:
Infine:
dove:
- nel passaggio (*) abbiamo sostituito tutti i termini che precedono la sommatoria con O(x) (i termini con la funzione \overline{\psi} sono O(x) per il Teorema N.4, come già osservato nel dettaglio precedente);
- nel passaggio (**) applicato la formula (h) del dettaglio precedente
- nel passaggio successivo abbiamo applicato, come di consueto, la Proprietà A.10 e il Corollario della Proprietà A.9.
Abbiamo così completato la dimostrazione della (9).
La Proposizione N.12 è rappresentata nel grafico seguente, dove il termine O(x \log x) sembra essere poco più piccolo in valore assoluto della funzione -\frac{5}{2} \log x.
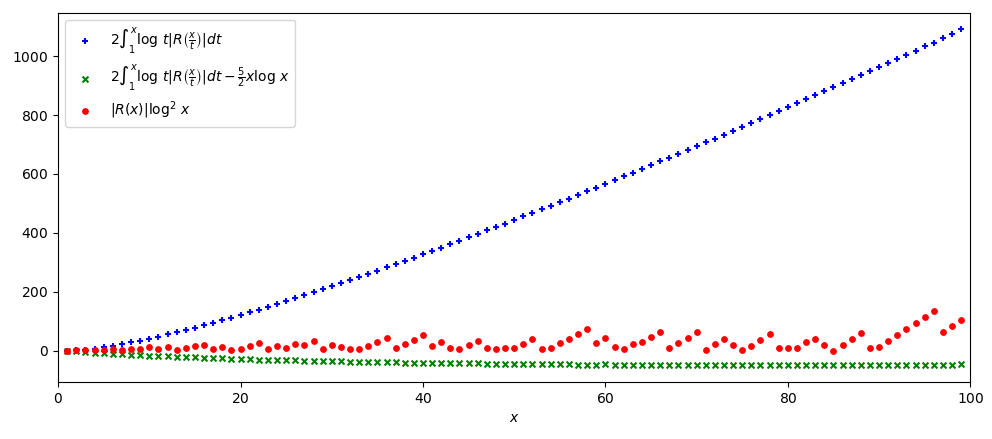
Osserviamo che la funzione \int_1^x \log t \left| R\left(\frac{x}{t}\right) \right| dt che compare nella Proposizione N.12 non è la classica funzione integrale del tipo g(x) := \int_a^x f(t) dt. Nel caso di questa funzione g, la funzione integranda non varia al variare di x, quindi per x = 1, 2, 3, \ldots si ottengono i valori g(1) = \int_a^1 f(t) dt,\ g(2) = \int_a^2 f(t) dt,\ g(3) = \int_a^3 f(t) dt, \ldots, che corrispondono, se f è non negativa, alle aree sottese al grafico di f limitatamente agli intervalli delle ascisse [a, 1],\ [a, 2],\ [a, 3], \ldots. Nella funzione \int_1^x \log t \left| R\left(\frac{x}{t}\right) \right| dt invece la x compare anche all’interno della funzione integranda, per cui la funzione di cui si calcola l’integrale cambia al variare di x: per x = 1, 2, 3, \ldots si ottengono i valori \int_1^1 \log t \left| R\left(\frac{1}{t}\right) \right| dt, \int_1^2 \log t \left| R\left(\frac{2}{t}\right) \right| dt, \int_1^3 \log t \left| R\left(\frac{3}{t}\right) \right| dt, \ldots. I valori mostrati in Figura 2 sono stati ottenuti calcolando numericamente questi integrali. Lo stesso discorso vale anche per la Figura 1.