
Prerequisito: Numeri primi e fattorizzazione (basi scolastiche)
Cominciamo il nostro studio dei numeri primi chiarendo proprio la definizione di numero primo. Ciò che comunemente si sa è che un numero primo è un numero intero positivo divisibile solo per se stesso e per 1. Questo è vero tranne che per il numero 1, che in base a ciò dovrebbe essere primo (1 è divisibile per 1, che è anche se stesso), ma in realtà non lo è. Il numero 1 infatti si esclude a priori dai numeri primi. Il motivo è legato al seguente teorema, detto Teorema Fondamentale dell’Aritmetica:
Teorema fondamentale dell’aritmetica
Ogni numero intero maggiore di 1 si può scrivere come prodotto di numeri primi. Inoltre tale scrittura, chiamata fattorizzazione o scomposizione in fattori primi, è unica a meno dell’ordine dei fattori.
| 150 | 2 |
| 75 | 3 |
| 25 | 5 |
| 5 | 5 |
| 1 |
I passaggi applicati sono i seguenti:
- Si parte da 150, lo si scrive in cima alla colonna di sinistra, e lo si divide per il più piccolo numero primo che sia suo divisore, ossia 2, ottenendo 75; si scrive il divisore ottenuto in cima alla colonna di destra;
- Il risultato della divisione viene riportato a sua volta nella colonna di sinistra e si ripete la procedura su di esso, dividendolo di volta in volta per il più piccolo numero primo possibile che sia suo divisore;
- Quando il risultato della divisione è 1, la procedura termina;
- Alla fine si ha 150 = 2 \cdot 3 \cdot 5 \cdot 5. Questo risultato può essere scritto anche in modo più compatto, considerando che il prodotto di un numero per se stesso, per definizione, corrisponde a una potenza: 150 = 2 \cdot 3 \cdot 5^2.
Se il numero di partenza è piccolo e i fattori primi da trovare sono pochi, l’operazione è molto semplice, ma non sempre è così. Come si può verificare con il fattorizzatore, ad esempio, un numero relativamente piccolo come 1024 necessita di molte divisioni, e numeri formati da fattori primi grandi, come 89077, richiedono diversi tentativi per trovare un numero primo che ne sia divisore. Se poi i fattori primi sono estremamente grandi, trovarli diventa una vera sfida, come ha ampiamente dimostrato la RSA Factoring Challenge, che consisteva proprio nel partire da alcuni numeri ottenuti come prodotto di due numeri primi noti molto grandi (non rivelati dagli organizzatori) e tentare di fattorizzarli: per alcuni di essi, finora, è stato impossibile riuscirci.
Se 1 fosse considerato primo, il Teorema fondamentale dell’Aritmetica non sarebbe valido così com’è e dovrebbe essere espresso diversamente, aggiungendo un’eccezione. Di conseguenza, una miriade di teoremi che, direttamente o indirettamente, dipendono da esso dovrebbero essere modificati a loro volta, introducendo delle eccezioni spesso scomode… di fatto la cosa più semplice è assumere che 1 non sia primo.
Il prodotto di cui si parla nell’enunciato del Teorema Fondamentale dell’Aritmetica può essere formato da un qualsiasi numero k di fattori primi, non necessariamente distinti. Ad esempio 12 = 2 \cdot 2 \cdot 3 è il prodotto di k = 3 numeri primi. Normalmente il prodotto è definito per almeno k = 2 fattori, tuttavia per la teoria che ci apprestiamo a sviluppare sarà comodo estendere il concetto di prodotto considerando il caso del prodotto un solo fattore (k = 1), che è il fattore stesso. Adottando questa convenzione, anche un numero primo è prodotto di numeri primi: un prodotto speciale, costituito dal numero stesso che non moltiplica nessun altro. Ad esempio, ecco le fattorizzazioni dei numeri da 2 a 10:
| Numero | Fattorizzazione | Numero di fattori |
|---|---|---|
| 2 | 2 | 1 |
| 3 | 3 | 1 |
| 4 | 2 \cdot 2 | 2 |
| 5 | 5 | 1 |
| 6 | 2 \cdot 3 | 2 |
| 7 | 7 | 1 |
| 8 | 2 \cdot 2 \cdot 2 | 3 |
| 9 | 3 \cdot 3 | 2 |
| 10 | 2 \cdot 5 | 2 |
Il Teorema fondamentale dell’aritmetica afferma non solo che ogni numero intero maggiore di 1 ammette una fattorizzazione in fattori primi, ma anche che tale fattorizzazione è unica a meno dell’ordine dei fattori. Ad esempio 12 = 2 \cdot 2 \cdot 3 e non esistono altri numeri primi, a parte il 2 preso due volte ed il 3 preso una volta, che moltiplicati tra loro fanno 12. L’unicità della fattorizzazione è una proprietà fondamentale che è alla base di molti teoremi di teoria dei numeri, ed è proprio qui che possiamo capire perché 1 non è considerato un numero primo. Infatti, se 1 fosse primo, ogni numero intero positivo avrebbe infinite fattorizzazioni in fattori primi. Ad esempio
Per evitare ciò, ed essere certi di avere sempre un’unica fattorizzazione, 1 non è considerato primo. Per questo il teorema fondamentale dell’aritmetica vale per gli interi maggiori di 1: non può valere per 1, perché non è primo ed è prodotto solo di se stesso, quindi non è prodotto di primi.
Avendo escluso il numero 1 dai numeri primi, possiamo enunciare una definizione corretta di numero primo:
Numero primo
Un numero primo è un numero intero maggiore di 1 che è divisibile solo per se stesso e per 1.
Questa definizione fa riferimento al concetto di divisibilità, che è bene precisare:
Divisibilità
Un intero a è divisibile per un intero b, con b \neq 0, se a = b c per qualche intero c.
Se a è divisibile per b si scrive b \mid a (“b divide a“), altrimenti si scrive b \nmid a (“b non divide a“).
Ad esempio, 10 è divisibile per 2 perché si può scrivere come 10 = 2 \cdot 5, dove 5 è un intero c tale che 10 = 2 \cdot c. Al contrario, 10 non è divisibile per 3 perché non esiste alcun intero c tale che 10 = 3 \cdot c. In altri termini, si può dire che 2 divide 10 (2 \mid 10) e 3 non divide 10 (3 \nmid 10).
Dalla Definizione N.2 si esclude il caso di b = 0, perciò resta non definito il fatto che un numero sia divisibile per 0 oppure no.
Una conseguenza immediata della definizione di divisibilità è la seguente:
Nei numeri naturali, un divisore è minore o uguale di un dividendo positivo
Siano a e b due numeri naturali, con a \gt 0. Se b \mid a, allora b \leq a.
Se b \mid a, per la Definizione N.2 esiste un intero c tale che bc = a. Per la regola del prodotto dei segni, questo intero deve essere positivo, perché per ipotesi a e b sono numeri naturali, dunque positivi. Inoltre, c non può essere nullo, perché se così fosse sarebbe a = bc = b \cdot 0 = 0, ma per ipotesi deve essere a \gt 0. Quindi c \geq 1. Allora b = b \cdot 1 \leq bc = a, da cui b \leq a.
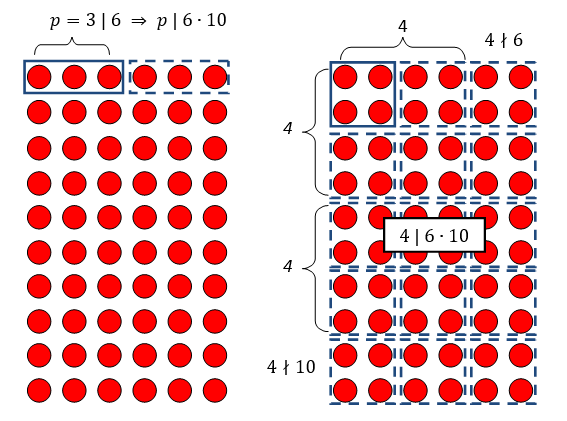
La divisibilità ha molto a che fare con la fattorizzazione in fattori primi: infatti, se b \mid a – cioè a = b c per qualche intero c – vuol dire che in qualche modo b compare nella fattorizzazione di a, come primo o come prodotto di numeri primi. Ad esempio:
- 2 \mid 10 e 2 compare nella fattorizzazione di 10 come numero primo: 10 = \mathbf{2} \cdot 5;
- 6 \mid 24 e 6 compare nella fattorizzazione di 24 come prodotto di numeri primi: 24 = 2 \cdot 2 \cdot \mathbf{2 \cdot 3};
- Anche 8 \mid 24 e 8 compare nella fattorizzazione di 24 come prodotto di numeri primi: 24 = \mathbf{2 \cdot 2 \cdot 2} \cdot 3;
Quindi se b \mid a vuol dire che la fattorizzazione di b è contenuta nella fattorizzazione di a. In particolare, se un numero primo p \mid a, p deve essere uno dei primi presenti nella fattorizzazione di a. Ad esempio, se a = p_1 p_2, con p_1 e p_2 primi, deve essere p = p_1 oppure p = p_2. Questa semplice proprietà caratterizza così fortemente i numeri primi che, opportunamente generalizzata, può essere presa come definizione alternativa di numero primo:
Numero primo, proprietà caratteristica o definizione alternativa
Un numero primo è un numero intero p > 1 tale che, se p \mid bc, allora p \mid b oppure p \mid c, per qualunque coppia di interi b e c. In altri termini, p non può dividere un prodotto di interi bc senza dividere almeno uno dei due fattori.
Chiaramente, se scegliessimo questa come definizione di numero primo, la Definizione N.1 diventerebbe una proprietà da dimostrare sulla base della Proprietà N.1B. Invece, dato che abbiamo scelto come definizione di numero primo la Definizione N.1, allora quest’ultima è il punto di partenza per dimostrare la Proprietà N.1B. Non vedremo questa dimostrazione, ma cerchiamo di chiarire l’enunciato. Scomponiamo il numero bc in fattori primi: ad esempio se b = 6 e c = 10, bc = 60 e si ha
Ma essendo 60 il prodotto di 6 e di 10, possiamo riordinare la sua fattorizzazione in modo da trovare i fattori di 6 ed i fattori di 10:
Per il ragionamento di prima, se p è un numero primo che divide 60, p deve comparire nella sua fattorizzazione (cioè p = 2 o p = 3 o p = 5); ma allora, per come la abbiamo suddivisa, p deve far parte o della fattorizzazione di 6 (cioè p = 2 o p = 3), ed in tal caso dividerebbe 6, oppure della fattorizzazione di 10 (cioè p = 2 o p = 5), ed in tal caso dividerebbe 10. Eventualmente p può trovarsi in entrambe le fattorizzazioni, come il caso di p = 2, ma deve trovarsi in almeno una di esse. Per capirlo meglio, possiamo immaginare di applicare il seguente algoritmo: scorriamo la lista dei fattori primi di 60 nell’ordine della (1): 2, 3, 2, 5; se troviamo p nelle prime due posizioni, diciamo che p \mid 6; altrimenti diciamo che p \mid 10. In questo modo, se p non è un divisore di 60 non lo troveremo e non daremo nessuna risposta; se invece p \mid 60 lo troveremo in una o più posizioni e daremo almeno una delle risposte “p \mid 6” e “p \mid 10“.
È altrettanto interessante osservare cosa succede nel caso di un numero non primo (che si dice composto), come 4. Abbiamo che 4 \mid 60, quindi la fattorizzazione di 4 deve essere contenuta in quella di 60. Ma 4 non è primo, perciò 4 non può trovarsi nella fattorizzazione di 60 come numero primo, ma deve trovarsi nella forma di un prodotto di numeri primi. Questo fa sì che 4 divida 60 senza dividere né 6 né 10, come si può vedere evidenziando i fattori primi di 4 (2 \cdot 2) nella (1):
Possiamo vedere che il 4 si “spezza” in un 2 che compare tra i divisori di 6, ed un altro 2 che compare tra i divisori di 10: perciò 4 non divide né 6 né 10, pur dividendo il loro prodotto 60. Questo non può accadere con un numero primo, perché un numero primo non può “spezzarsi” tra i due fattori b e c: deve trovarsi “integro” in uno dei due.
L’ultimo esempio è illustrato graficamente nell’immagine sottostante:
I numeri primi sono infiniti
Un teorema, ben noto fin dall’antichità, che deriva dalle definizioni di sopra e dal Teorema Fondamentale dell’Aritmetica, è il seguente:
Infinità dei numeri primi
I numeri primi sono infiniti.
La dimostrazione è così famosa e semplice che vale la pena di essere ricordata. Supponiamo che esista solo un certo numero finito N di numeri primi. Se così fosse, potremmo elencare tutti i numeri primi in ordine crescente: p_1, p_2, \ldots, p_N, dove p_N è il più grande numero primo. Allora, partendo da questo elenco di numeri primi, possiamo costruire il numero
Per come è definito, questo numero non è divisibile per nessuno dei primi p_1, p_2, ..., p_N.
Poniamoci la domanda: per quali numeri primi è divisibile M? Vediamo ad esempio se è divisibile per p_1. Se così fosse, per la Definizione N.2 (Divisibilità) dovrebbe esistere un intero c tale che
Da cui, raccogliendo p_1, si avrebbe che
Da cui, sempre per la Definizione N.2, p_1 \mid 1. Allora per la Proprietà N.1A, dovrebbe essere p_1 \leq 1; ma questo non è possibile perché i numeri primi, per la Definizione N.1, devono essere maggiori di 1. Ciò significa che l’ipotetico numero c dell’equazione (4) non può esistere, ossia M non è divisibile per p_1.
Questo ragionamento non dipende dal fatto di aver scelto p_1, infatti può essere ripetuto anche per tutti gli altri primi p_2, \ldots, p_N, col risultato che M non è divisibile per nessuno dei primi p_1, p_2, \ldots, p_N.
Per il Teorema Fondamentale dell’Aritmetica, M è fattorizzabile come prodotto di numeri primi. Per la Definizione N.2, tutti i numeri primi presenti nella fattorizzazione di M lo dividono; quindi, per quanto detto prima, non possono essere uguali a nessuno dei primi p_1, p_2, ..., p_N. Ma questo è assurdo, perché abbiamo supposto che p_1, p_2, ..., p_N sono gli unici numeri primi esistenti. Ciò significa che l’ipotesi di partenza, che esista un numero finito di numeri primi, è errata: i numeri primi sono infiniti.