Le nostre ricerche sulla Congettura di Goldbach ci hanno portato, a un certo punto, ad estendere la definizione di tratteggio lineare. Come sappiamo, un tratteggio lineare è una funzione rappresentata da una tabella con k righe e infinite colonne numerate a partire da 1, dove in ciascuna riga compare un trattino per ogni colonna il cui numero è multiplo di un certo intero positivo fissato (una delle componenti del tratteggio). A volte è necessario considerare tabelle in cui i trattini compaiono non solo in corrispondenza dei multipli, ma anche in corrispondenza dei numeri che hanno un certo resto fissato, modulo una o più componenti.
Ad esempio, partiamo dal tratteggio (2, 3, 5, 7) rappresentato fino a 25:
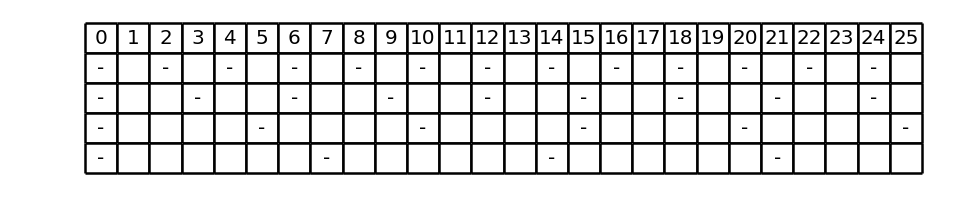
Per definizione, sulla prima riga compaiono i trattini in corrispondenza dei multipli di 2, sulla seconda riga in corrispondenza dei multipli di 3, sulla terza riga in corrispondenza di quelli di 5, sulla quarta riga in corrispondenza di quelli di 7.
Ora proviamo a modificare il tratteggio in questo modo:
- Lasciamo la prima e la terza riga così come sono;
- Sulla seconda riga, la cui componente è 3, aggiungiamo dei trattini in corrispondenza dei numeri che hanno resto 1 modulo 3;
- Sulla quarta riga, la cui componente è 7, aggiungiamo dei trattini in corrispondenza dei numeri che hanno resto 2 modulo 7.
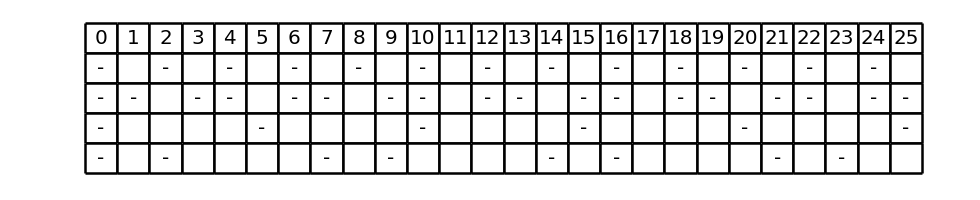
Quello che abbiamo ottenuto è un esempio di quello che chiameremo “doppio tratteggio”. In un doppio tratteggio, quindi, possono esistere righe identiche a quelle dei tratteggi lineari, coi trattini solo in corrispondenza dei multipli, e righe dove i trattini compaiono sia in corrispondenza dei multipli della relativa componente (cioè i numeri che hanno resto 0 modulo la componente), sia in corrispondenza dei numeri che hanno un certo resto, diverso da zero, modulo la componente. Se, come nelle Figure precedente, si parte da un tratteggio lineare T per ottenere un doppio tratteggio che conserva i trattini di T e ne aggiunge degli altri, allora il doppio tratteggio si dice “basato su T“.
Per rafforzare la contrapposizione con i doppi tratteggi, a volte i tratteggi lineari sono chiamati anche tratteggi singoli. Sia i tratteggi doppi che quelli singoli rientrano nella definizione generale di tratteggio, che è volutamente molto generica, in modo tale che sia possibile costruire classi diverse di tratteggi a seconda delle proprie esigenze. Così come nei tratteggi singoli le componenti possono essere scelte in modo arbitrario, nei doppi tratteggi i resti possono essere scelti a piacere, ad esempio possono non essere tutti diversi
Se volessimo scrivere la funzione matematica corrispondente al tratteggio della Figura 2, che possiamo chiamare U, otterremmo qualcosa di simile alla seguente:
In generale, partendo da un generico tratteggio lineare T, si ottiene la seguente definizione di doppio tratteggio, che riprende ed estende le Definizioni T.1 (Tratteggio) e T.2 (Tratteggio lineare):
Doppio tratteggio lineare
Sia T = (n_1, \ldots, n_k) un tratteggio lineare di ordine k con insieme degli indici I. Siano r_1, \ldots, r_k degli interi tali che, per ogni i = 1, \ldots, k, 0 \leq r_i \lt n_i. Si definisce allora il tratteggio T^{(r_1, \ldots, r_k)}: I \times \mathbb{N} \Rightarrow \mathbb{N} tale che:
Esso si dice doppio tratteggio lineare (o semplicemente doppio tratteggio) basato su T, con spiazzamenti r_1, \ldots, r_k.
I tecnicismi della definizione non sono importanti; è importante invece ricordare che i numeri r_1, \ldots, r_k sono detti spiazzamenti e sono i resti aggiuntivi in base ai quali, su ciascuna riga, vengono inseriti ulteriori trattini rispetto al tratteggio lineare di partenza. In particolare, le righe in cui non sono stati inseriti trattini aggiuntivi si considerano come aventi spiazzamento 0: ad esempio, se indichiamo il tratteggio della Figura 1 con T, allora il tratteggio della Figura 2 si chiama “doppio tratteggio basato su T con spiazzamenti 0, 1, 0, 2” e si indica con T^{(0, 1, 0, 2)}. Osserviamo che, quando r_i = 0, la riga i del doppio tratteggio coincide con quella del tratteggio lineare di partenza, ossia non ha trattini aggiuntivi, come si vede in questo esempio per i = 1 e i = 3.
Come accennavamo all’inizio, i doppi tratteggi sono importanti per lo studio della Congettura di Goldbach. Per approfondire questo aspetto, rimandiamo i lettori alla strategia dimostrativa basata sugli spazi.