Prerequisiti:
- La funzione fattoriale
- Parte intera di un numero reale
- Il minimo comune multiplo dei primi numeri interi positivi
- Elementi di analisi asintotica
- Teorema N.4 (Equivalenza asintotica e ordine di grandezza di \theta(x) e \psi(x))
- Dai numeri interi ai numeri reali – seconda parte
Quasi certamente conoscete già la funzione fattoriale, indicata con x!, che si legge “x fattoriale” e per un intero x \gt 0 consiste nel prodotto di tutti i numeri interi positivi fino ad x:
Inoltre, ricordiamo che si pone 0! = 1, coerentemente con la nostra usuale assunzione che il prodotto di un insieme vuoto di numeri sia 1.
La funzione fattoriale è utilizzata soprattutto nel calcolo combinatorio; ma il calcolo combinatorio è uno dei fondamenti della teoria dei numeri (v. ad esempio l’articolo 3. Il prodotto dei primi numeri primi: una maggiorazione), per cui non deve stupire che il fattoriale ricorra spesso anche in teoria dei numeri. In questo articolo studieremo il fattoriale da due diversi punti di vista: dapprima ne studieremo l’ordine di grandezza; successivamente scomporremo il prodotto (1) in modo da evidenziare i fattori primi che lo compongono.
Ordine di grandezza
Dire che la funzione fattoriale cresce velocemente è dire poco: ad esempio, 10! è ben 3.628.800, e 50! è un numero di 65 cifre. Le tecniche chiave per studiare una funzione del genere sono due:
- Confrontare la funzione fattoriale con un’altra funzione che cresce altrettanto velocemente, ma più semplice
- Passare ai logaritmi. Infatti la funzione logaritmo ha due buone proprietà:
- abbassa notevolmente il tasso di crescita di una funzione
- trasforma i prodotti in somme, che sono più facili da studiare
Una funzione più semplice del fattoriale, con un tasso di crescita simile, è la funzione x^x. La maggiore semplicità deriva dal fatto che, invece di variare i fattori del prodotto, questa funzione ripete x volte il prodotto dello stesso numero x:
Confrontando la (1) con la (2) si vede immediatamente che x^x è maggiore di x!, ma di quanto è maggiore? Per capirlo, studiamo il rapporto:
Ora introduciamo i logaritmi:
La funzione così ottenuta è esattamente quella che abbiamo visto nell’articolo precedente. Essa, per il Lemma N.6, è un O grande di x, per cui:
Oppure equivalentemente, rimuovendo i logaritmi:
Da questa uguaglianza si può ottenere l’ordine di grandezza del fattoriale:
L’ultimo passaggio si giustifica col fatto che O(x) = -O(x). Per capire questa uguaglianza, dobbiamo ricordare che O(x) rappresenta una funzione sia a destra che a sinistra, per cui O(x) = -O(x) significa due cose:
- O(x) \subset -O(x), cioè per ogni funzione f = O(x) esiste una funzione g = O(x) tale che f = -g
- -O(x) \subset O(x), cioè per ogni funzione f = O(x) esiste una funzione g = O(x) tale che -f = g
In realtà la questione è piu semplice di quanto possa sembrare, perché evidentemente questa g non è altro che -f, per cui nel primo caso è sufficiente dimostrare che f = O(x) \Rightarrow -f = O(x); inoltre il secondo caso è equivalente al primo, perché f = -g \Leftrightarrow -f = g, per cui non va dimostrato nient’altro.
Ricordando la definizione di f = O(x), ossia che definitivamente -Ax \leq f(x) \leq Ax per qualche costante A \geq 0 (v. Definizione A.3 (Relazioni asintotiche, definizioni alternative utilizzando le disuguaglianze)), possiamo dimostrare l’implicazione f = O(x) \Rightarrow -f = O(x), concludendo così la dimostrazione:
Possiamo quindi enunciare la seguente Proposizione:
Ordine di grandezza del fattoriale
Da questa formula si ottiene:
Dunque il rapporto (3), che nella (4) abbiamo espresso più genericamente nella forma e^{O(x)}, in realtà è asintoticamente equivalente a \frac{e^x}{2 \pi x}. Per i nostri scopi però non è necessario utilizzare la formula di Stirling, ma è sufficiente la Proposizione N.5.
Il fattoriale e la funzione \Lambda^{\star}
Finora abbiamo studiato l’ordine di grandezza del fattoriale, ma cosa possiamo dire del suo valore esatto? Vediamo a tal proposito una costruzione che ci può aiutare a guardare il fattoriale da un altro punto di vista.
Supponiamo di voler calcolare il fattoriale di un intero x \gt 0. Costruiamo una tabella formata da x righe ed altrettante colonne, numerate da 1 ad x. Popoliamo la tabella in questo modo: nella cella che si trova all’incrocio tra la colonna c e la riga r scriviamo, solo se r \mid c, il numero
- p, se r = p^m per qualche primo p e qualche intero m \gt 0
- 1, altrimenti
In altri termini, scriviamo p se nella fattorizzazione di r compare un solo primo p, mentre scriviamo 1 se non compare nessun numero primo, cioè se r = 1, o compaiono più numeri primi diversi.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | ||||||||
| 3 | 3 | 3 | 3 | 3 | 3 | ||||||||||
| 4 | 2 | 2 | 2 | ||||||||||||
| 5 | 5 | 5 | 5 | ||||||||||||
| 6 | 1 | 1 | |||||||||||||
| 7 | 7 | 7 | |||||||||||||
| 8 | 1 | ||||||||||||||
| 9 | 3 | ||||||||||||||
| 10 | 1 | ||||||||||||||
| 11 | 11 | ||||||||||||||
| 12 | 1 | ||||||||||||||
| 13 | 13 | ||||||||||||||
| 14 | 1 | ||||||||||||||
| 15 | 1 |
Infatti:
- 1 non è la potenza di nessun numero primo, per cui nella sua riga compare sempre 1
- Nella fattorizzazione di 6, 10, 12, 14, 15 compaiono più numeri primi distinti, per cui nelle righe corrispondenti scriviamo sempre 1
- Nella fattorizzazione di 2, 3, 4, 5, 7, 8, 9, 11, 13 compare un solo numero primo distinto, cioè questi numeri sono della forma p^m con m \gt 0, per cui nelle righe corrispondenti scriviamo questo primo p
La tabella così ottenuta presenta una fondamentale proprietà: per ogni colonna c, il prodotto dei numeri all’interno della colonna è pari a c stesso. Ad esempio, con riferimento all’esempio precedente, nella colonna 12 abbiamo 1, 2, 3 e di nuovo 2, infatti 12 = 1 \cdot 2 \cdot 3 \cdot 2.
Per dimostrare questa proprietà, dobbiamo ricordare innanzitutto che abbiamo scritto un numero nella cella (r, c), appartenente alla riga r e alla colonna c, se e solo se r \mid c. Quindi all’interno della colonna c saranno piene solo le celle delle righe che sono divisori di c. Ora scomponiamo c in fattori primi:
dove q_1, q_2, \ldots, q_h sono i primi distinti che compaiono nella fattorizzazione di c, per cui i relativi esponenti m_1, m_2, \ldots, m_h sono tutti maggiori di zero.
Consideriamo ora un divisore d di c. Avendo scritto c nella forma (6), d si può scrivere nella forma
Cioè nella fattorizzazione di d possono comparire solo i numeri primi presenti nella fattorizzazione di c e, se compaiono, essi hanno un esponente minore o uguale di quello che hanno nella fattorizzazione di c. Infatti, il fatto che un primo q_i compaia o meno nella fattorizzazione di d è regolato dal relativo esponente n_i: se n_i = 0 allora q_i non compare, mentre se 0 \lt n_i \leq m_i esso compare con esponente al massimo pari a quello che ha nella fattorizzazione di c.
Il fatto che d si possa scrivere nella forma (7) si può dimostrare per contrapposizione. Se non fosse possibile scrivere d nella forma (7), vorrebbe dire che o la sua fattorizzazione contiene primi che non compaiono in quella di c; oppure contiene un primo che compare in entrambe le fattorizzazioni, ma l’esponente di questo primo nella fattorizzazione di d è più grande di quello che esso ha nella fattorizzazione di c. Ma in nessuno di questi casi d sarebbe un divisore di c. Quindi, dato che negando la (7) si ottiene che d non è un divisore di c, viceversa, se d è un divisore di c, vale la formula (7).
Avendo scritto d in questo modo, possiamo distinguere tre casi:
- n_1 = n_2 = \ldots = n_h = 0. In questo caso d = 1, quindi nella cella (d, c) = (1, c) compare il numero 1.
- Almeno due tra n_1, n_2, \ldots, n_h sono maggiori di zero. In questo caso la fattorizzazione di d contiene almeno due fattori primi distinti, per cui nella cella (d, c) compare il numero 1.
- Solo uno tra n_1, n_2, \ldots, n_h è maggiore di zero. In questo caso d = q_i^{n_i} per qualche i, quindi nella cella (d, c) compare il numero q_i.
È evidente che solo il terzo caso influisce sul prodotto dei numeri posti all’interno della colonna c, perciò concentriamoci su di esso. Quante volte può presentarsi questo caso? Rispondere a questa domanda equivale a chiedersi quanti divisori di c del tipo d = q_i^{n_i}, con n_i \gt 0, esistano. Il conteggio è semplice, perché q_i può variare tra q_1 e q_h, mentre, per ogni scelta di q_i, il relativo esponente n_i può variare tra 1 ed m_i. Si hanno quindi m_1 possibilità per q_1, m_2 possibilità per q_2, …, m_h possibilità per q_h, per cui i casi possibili sono m_1 \cdot m_2 \cdot \ldots \cdot m_h. Scriviamoli esplicitamente:
- d = q_1^{n_1}, 0 \lt n_1 \leq m_1: sono gli m_1 divisori d = q_1, d = q_1^2, \ldots, d = q_1^{m_1}: in tutti questi casi nella cella (d, c) compare il numero q_1
- d = q_2^{n_2}, 0 \lt n_2 \leq m_2: sono gli m_2 divisori d = q_2, d = q_2^2, \ldots, d = q_2^{m_2}: in tutti questi casi nella cella (d, c) compare il numero q_2
- …
- d = q_h^{n_h}, 0 \lt n_h \leq m_h: sono gli m_h divisori d = q_h, d = q_h^2, \ldots, d = q_h^{m_h}: in tutti questi casi nella cella (d, c) compare il numero q_h
Quindi, ricapitolando:
- Nella cella (r, c) compare un numero solo quando r = d, dove d è un divisore di c
- Le m_1 celle (q_1, c), (q_1^2, c), …, (q_1^{m_1}, c) contengono il numero q_1
- Le m_2 celle (q_2, c), (q_2^2, c), …, (q_2^{m_2}, c) contengono il numero q_2
- …
- Le m_h celle (q_h, c), (q_h^2, c), …, (q_h^{m_h}, c) contengono il numero q_h
- Nessun’altra cella contiene un numero diverso da 1, perché non esistono altri divisori di c nella cui fattorizzazione compare un solo numero primo distinto
Da ciò si evince che il prodotto dei numeri che compaiono nella colonna c è q_1^{m_1} \cdot q_2^{m_2} \cdot \ldots q_h^{m_h}; ma questo prodotto, per la (6), è proprio c, come volevamo dimostrare.
Ma se il prodotto dei numeri all’interno di una qualsiasi colonna, da 1 a x, è pari al numero della colonna stessa, allora il prodotto dei numeri di tutte le colonne, cioè il prodotto di tutti i numeri presenti all’interno della tabella, è pari a 1 \cdot 2 \cdot \ldots \cdot x = x!.
Ora concentriamoci su quest’ultimo prodotto, quello di tutti i numeri della tabella. Esso evidentemente non cambia se, invece di leggere i numeri per colonne, li leggiamo per righe: così facendo si ottiene una formula abbastanza interessante.
Per come abbiamo costruito la tabella, su una stessa riga r compare sempre lo stesso numero, che chiameremo \Lambda^{\star}(r), ponendo x := r nella seguente Definizione generale:
Funzione \Lambda^{\star}
Si definisce la funzione \Lambda^{\star}: \mathbb{N}^{\star} \rightarrow \mathbb{N}^{\star} tale che:
Ma quante volte il numero \Lambda^{\star}(r) compare sulla riga r? Esso compare in corrispondenza delle colonne aventi per numero un multiplo di r, quindi in totale compare tante volte quanti sono i multipli di r compresi nell’intervallo [1, x]. Questo numero si può calcolare con una semplice formula:
Numero di multipli di un dato numero, compresi tra 1 ed x
Siano n ed x due interi positivi. Il numero di multipli di n compresi nell’intervallo [1, x] è \left \lfloor \frac{x}{n} \right \rfloor.
Se dividiamo x per n, abbiamo che esistono due interi q ed r (rispettivamente, il quoziente ed il resto) tali che:
Quindi esistono certamente q multipli di n nell’intervallo [1, x]: n, 2n, \ldots, qn. Questi infatti sono tutti numeri positivi minori o uguali a qn, che a sua volta, per la (8), è minore o uguale di x. Vediamo se esiste qualche altro multiplo di n nell’intervallo [1, x]. Possiamo ovviamente scartare i multipli negativi e lo zero, che certamente non rientrano nell’intervallo. Per quanto riguarda invece il multiplo (q + 1)n, esso è maggiore di x, in quanto (q + 1)n = qn + n \gt qn + r = x. Quindi a maggior ragione anche qualunque altro multiplo hn, con h \gt q, è maggiore di x. Allora esistono esattamente q multipli di n nell’intervallo [1, x], ed essi sono n, 2n, \ldots, qn.
Ma q, il quoziente della divisione di x per n, coincide di fatto con la parte intera approssimata per difetto della divisione stessa, cioè \left \lfloor \frac{x}{n} \right \rfloor. Per dimostrarlo, dobbiamo ricordare che la parte intera di un numero reale t si definisce come il più grande numero intero minore o uguale di t. In questo caso t := \frac{x}{n}, e q è un intero minore o uguale di \frac{x}{n}; infatti, per la (8):
Inoltre q è il più grande intero minore o uguale di \frac{x}{n}; infatti l’intero successivo, q + 1, è maggiore di \frac{x}{n}:
dove nel passaggio \frac{x + n - r}{n} \geq \frac{x + 1}{n} abbiamo utilizzato il fatto che r \lt n, per la (8). Quindi, per definizione di parte intera, q = \left \lfloor \frac{x}{n} \right \rfloor e q, come abbiamo visto prima, è il numero di multipli di n nell’intervallo [1, x].
Ponendo n := r nella Proprietà N.5, abbiamo che esistono \left \lfloor \frac{x}{r} \right \rfloor multipli di r nell’intervallo [1, x], quindi \Lambda^{\star}(r) compare \left \lfloor \frac{x}{r} \right \rfloor volte sulla riga r. Allora il prodotto dei numeri sulla riga r è \left( \Lambda^{\star}(r) \right)^{\left \lfloor \frac{x}{r} \right \rfloor}, ed il prodotto di tutti i numeri della tabella è
Questo è il prodotto dei numeri della tabella calcolato per righe. Dato che esso deve coincidere con lo stesso prodotto calcolato per colonne, che come abbiamo visto prima è x!, abbiamo così dimostrato la seguente Proposizione:
Il fattoriale e la funzione \Lambda^{\star}
Per ogni intero x \gt 0,
Unendo la Proposizione N.5 con la Proposizione N.6, si ottiene che l’ordine di grandezza della funzione \prod_{r = 1}^x \left( \Lambda^{\star}(r) \right)^{\left \lfloor \frac{x}{r} \right \rfloor} è x^x e^{O(x)}. Questo può essere un punto di partenza per lo studio della funzione \Lambda^{\star}, tuttavia sarebbe meglio se non ci fosse la parte intera, perché questo operatore complica i calcoli. Allora ci possiamo chiedere: cosa succede se nella formula (9) togliamo la parte intera? Quanto il membro di destra si discosterebbe dal fattoriale? Vediamo.
Innanzitutto, dato che qualunque numero reale differisce dalla sua parte intera di meno di un’unità, si ha che
Quindi, se nella (9) togliamo la parte intera, otteniamo una quantità più grande, con un errore compreso nel seguente intervallo:
Partendo da questa disuguaglianza, sviluppando i calcoli ed utilizzando la Proposizione N.6, otteniamo:
Il prodotto \prod_{r = 1}^x \Lambda^{\star}(r) è molto interessante. Calcolare questo prodotto significa passare in rassegna tutti i numeri interi da 1 a x, e moltiplicare per un fattore p ogni volta che si trova una nuova potenza di un primo p. Così facendo, alla fine ogni primo p comparirà nel prodotto tante volte quanto è il numero delle sue potenze minori o uguali ad x. Ma se ci sono N potenze di p minori o uguali ad x, esse sono p, p^2, \ldots, p^N. Allora la massima potenza di p minore o uguale ad x è p^N, dunque N = \left \lfloor \log_p x \right \rfloor. Un esempio è mostrato nell’immagine seguente, per x = 9:
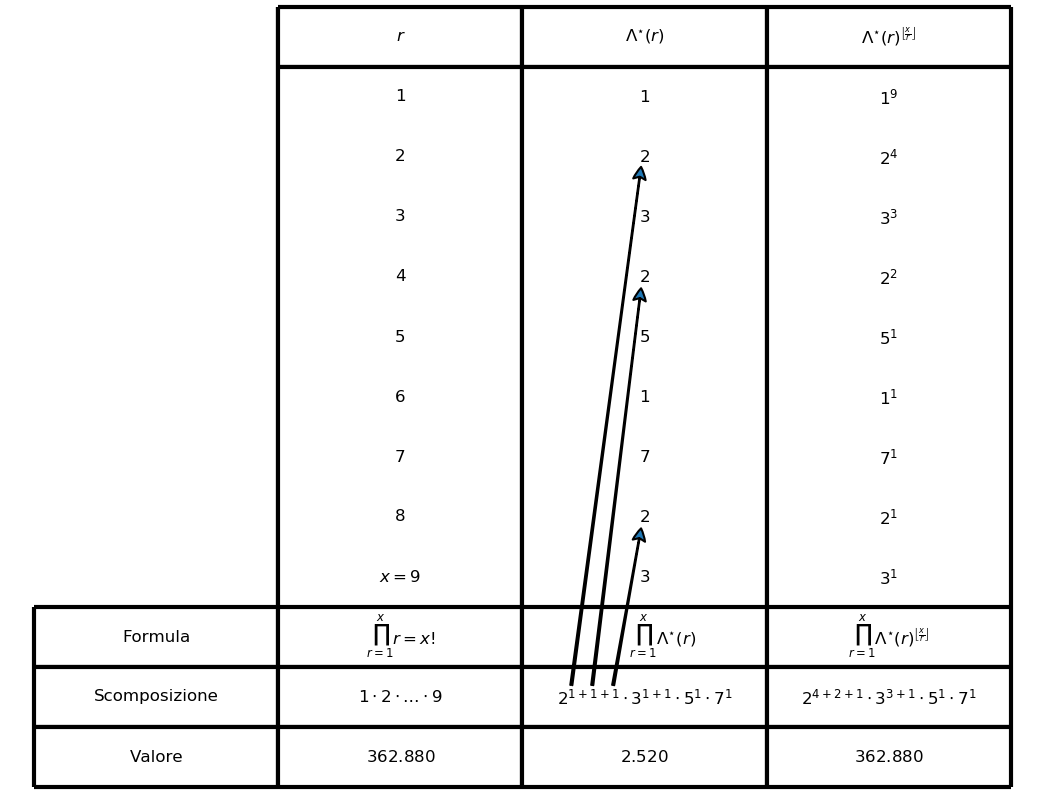
Quindi possiamo dire che:
Ricordate qual è la funzione a destra? Per la Proposizione N.2 (Calcolo di \psi^{\star}(x)), \prod_{p \leq x} p^{\left \lfloor \log_p x \right \rfloor} = \psi^{\star}(x): è la funzione che calcola il minimo comune multiplo dei numeri interi da 1 a x. Possiamo quindi enunciare la seguente Proprietà:
Connessione tra \Lambda^{\star} e \psi^{\star}
Per ogni intero x \gt 0:
Quindi, per la (10) e la Proprietà N.6:
Ma, per il Teorema N.4 (Equivalenza asintotica e ordine di grandezza di \theta(x) e \psi(x)), \log \psi^{\star}(x) = \psi(x) \asymp x, quindi in particolare \log \psi^{\star}(x) = O(x), da cui \psi^{\star}(x) = e^{O(x)}. Sostituendo nella (11) si ottiene:
Chiamiamo f la funzione che compare al primo membro della (11), per cui f(x) := \frac{\prod_{r = 1}^x \left( \Lambda^{\star}(r) \right)^{\frac{x}{r}}}{x!}. Per la (11) abbiamo che 1 \leq f(x) \lt \psi^{\star}(x), inoltre abbiamo visto che \psi^{\star}(x) = e^{O(x)}, per cui 1 \leq f(x) \lt e^{O(x)}. La domanda quindi è: da questa disuguaglianza si può concludere che f(x) = e^{O(x)}?
Per rispondere, ricordiamo che O(x) è per definizione una funzione g tale che definitivamente |g(x)| \leq Ax, ossia -Ax \leq g(x) \leq Ax, per qualche costante A \geq 0. Quindi una funzione e^{O(x)} è una funzione h tale che definitivamente e^{-Ax} \leq h(x) \leq e^{Ax}. Dobbiamo dimostrare che questa disuguaglianza vale per h := f. Partendo da 1 \leq f(x) \lt e^{O(x)}, essendo e^{O(x)} \leq e^{Ax}, abbiamo che:
Ma, essendo la funzione e^x crescente ed A \geq 0, abbiamo che e^{-Ax} \leq e^0 = 1, per cui
Quindi, per definizione, f(x) = e^{O(x)}, come volevamo dimostrare.
Osserviamo che, per raggiungere questo risultato, sono importanti entrambi i membri della disuguaglianza da cui siamo partiti, 1 \leq f(x) \lt e^{O(x)}. Se avessimo trascurato il fatto che 1 \leq f(x), non avremmo potuto concludere che f(x) = e^{O(x)}. Infatti questo non è vero, ad esempio, se f(x)[latex] è [latex]-x o un'altra funzione a valori sempre negativi.
Infine dalla (12), utilizzando la Proposizione N.5, si ottiene:
Riassumendo, possiamo enunciare la seguente Proposizione:
Ordine di grandezza della funzione simil-fattoriale basata su \Lambda^{\star}