Prerequisiti:
Nell’articolo Alcune sommatorie importanti abbiamo introdotto le sommatorie estese a coppie di variabili il cui prodotto divide una costante (Definizione N.21); ora vedremo come la funzione di Möbius permette di semplificare questo tipo di sommatorie. Otterremo alla fine una formula molto importante, detta formula di inversione di Möbius.
Semplificazione di doppie sommatorie mediante la funzione di Möbius
Nell’articolo Alcune sommatorie importanti abbiamo visto la seguente Proprietà, che per comodità riportiamo anche qui:
Terza forma equivalente per le sommatorie dove il prodotto degli indici divide una costante
Sia n un numero intero positivo. Sia f una qualunque funzione definita su \mathbb{N}^{\star} \times \mathbb{N}^{\star} (non importa l’insieme di arrivo(*)). Allora:
(*) Valgono le stesse considerazioni fatte per la Proprietà N.14
Nonostante l’apparente complessità, questa Proprietà è di uso abbastanza comune: il motivo è che, nella doppia sommatoria \sum_{d \mid n} \sum_{d^{\prime} \mid d} f\left(d^{\prime}, \frac{d}{d^{\prime}}\right), la sommatoria più interna potrebbe essere qualcosa di già noto. Prendiamo ad esempio la Proprietà N.12 (forma logaritmica):
Se ora vogliamo calcolare la sommatoria:
dobbiamo applicare la (1) mettendo d al posto di n, scegliendo di conseguenza un altro nome per la variabile d, per esempio d^{\prime}:
Sostituendo nella (2), si ha:
Ci siamo così ricondotti alla forma della Proprietà N.15, con f(x, y) := \mu(x) \log y. Possiamo quindi applicare la Proprietà N.15, concludendo che:
In sostanza, quindi, la Proprietà N.15 permette di semplificare le sommatorie quando se ne creano di doppie per effetto delle sostituzioni.
Ma non è ancora tutto. La sommatoria che abbiamo ottenuto, infatti, si può semplificare ulteriormente. Più in generale, si possono semplificare tutte le sommatorie del tipo:
Infatti, raccogliendo i termini con lo stesso argomento della funzione f, ed utilizzando la Proprietà N.11, si può dimostrare la seguente Proprietà:
Semplificazione mediante la funzione di Möbius di una doppia sommatoria estesa ai divisori di un numero intero positivo, e ai divisori dei divisori
Sia n un numero intero positivo. Sia f una qualunque funzione definita su \mathbb{N}^{\star} (non importa l’insieme di arrivo(*)). Allora:
(*) Valgono le stesse considerazioni fatte per la Proprietà N.13
Un esempio di questa Proprietà, per n = 12, è illustrato graficamente nella Figura 1, dove, per ciascun valore di d, la sommatoria \mu(d^{\prime}) f\left(\frac{d}{d^{\prime}}\right) è visualizzata disponendo i valori di f secondo il diagramma di Hasse di d (ricordiamo che il diagramma di Hasse è stato utilizzato nel precedente articolo).
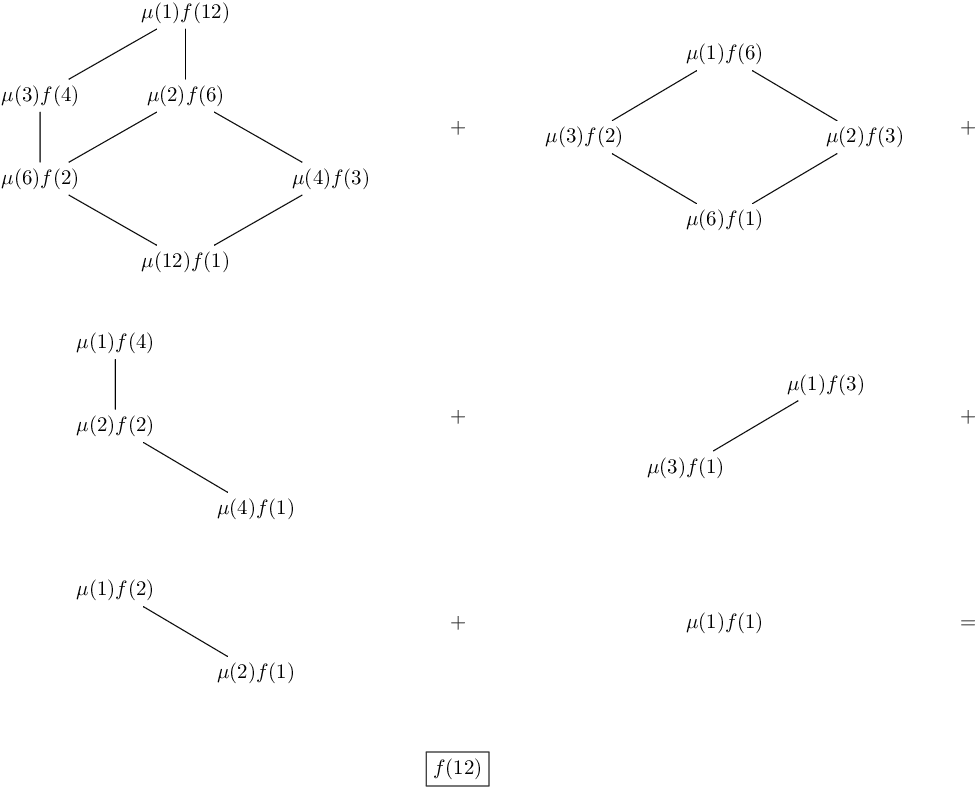
Per n = 12, la sommatoria (4) diventa:
Possiamo osservare che gli stessi valori della funzione f si ripetono diverse volte, moltiplicati per diversi valori di \mu, per cui possiamo metterli in evidenza. Così facendo, ciascuno di essi sarà moltiplicato per una sommatoria di valori di \mu. Ad esempio, il valore \boldsymbol{f(3)}, evidenziato in grassetto, compare moltiplicato per \mu(4), \mu(2) e \mu(1), per cui mettendolo in evidenza si otterrà \boldsymbol{f(3)}(\mu(1) + \mu(2) + \mu(4)).
Prima di proseguire la semplificazione della (d), è utile allineare i termini di righe diverse che hanno lo stesso argomento della funzione f:
A questo punto, per mettere in evidenza i termini f(\cdot) ripetuti dobbiamo semplicemente leggere quest’espressione per colonne invece che per righe. Così facendo, otteniamo:
Ma, per la Proprietà N.11, tutte le sommatorie di \mu(d) che abbiamo ottenuto sono nulle, tranne l’ultima che è uguale ad 1, per cui l’espressione precedente si riduce semplicemente a f(12).
Come abbiamo fatto nel precedente esempio, mettiamo in evidenza nella (10) i termini del tipo f(b). Innanzitutto, i possibili valori di b sono i divisori di n, per la relazione ab \mid n. Infatti, da b \mid ab e ab \mid n abbiamo che b \mid n; inoltre, se d è un divisore di n, possiamo porre b := d e a := \frac{n}{d}, ottenendo una coppia di valori ammessi per le variabili della sommatoria, perché ab = \frac{n}{d} d = n, quindi ab \mid n).
Fissiamo quindi un divisore d di n. Avendo appurato che d è uno dei possibili valori di b, chiediamoci ora quali sono i termini della sommatoria che hanno d come valore della variabile b. Se il generico termine della sommatoria è \mu(a) f(b), con ab \mid n, dobbiamo quindi cercare tutti i valori di a che danno luogo a termini del tipo \mu(a) f(d). Un tale termine compare nella sommatoria se e solo se ad \mid n, da cui a \mid \frac{n}{d}. Quindi, per b := d, tutti i possibili valori di a sono i divisori di \frac{n}{d}. Così facendo, al variare di d, esauriremo tutti i termini della sommatoria, per cui:
Nella sommatoria interna, in pratica, abbiamo raggruppato tutti i termini con f(d). Il passo successivo è metterli in evidenza:
Per la Proprietà N.11, la sommatoria interna è sempre uguale a zero, tranne quando \frac{n}{d} = 1, cioè quando d = n. Quindi:
Concatenando tutte le precedenti uguaglianze, si ottiene la (5).
La Proprietà N.16 è uno dei motivi per cui in teoria dei numeri si usano più spesso le somme rispetto ai prodotti: infatti, diversamente dalle Proprietà N.10 e N.12, non esiste una versione col prodotto di questa Proprietà (il motivo è che la dimostrazione si basa sulla Proprietà N.11, che a sua volta esiste solo con la somma).
Riprendendo la formula (3) ed applicando la Proprietà N.16 con f := \log, possiamo ottenere immediatamente una nuova proprietà della funzione \Lambda:
Espressione del logaritmo come sommatoria di \Lambda
Sia n un numero intero positivo. Allora:
Questa Proprietà è un esempio di applicazione della funzione di Möbius: la conoscenza di questa funzione e delle sue proprietà ci ha consentito di ottenerla in modo immediato, altrimenti avremmo dovuto dimostrarla separatamente.
La formula di inversione di Möbius
Confrontando le formule (1) e (6), si può notare che esse sono una l’inverso dell’altra, nel senso che:
- nella prima formula, la funzione \Lambda è espressa come una sommatoria di logaritmi (con opportuni coefficienti dati dalla funzione di Möbius);
- nella seconda formula, la funzione logaritmo è espressa come una sommatoria della funzione \Lambda.
Poiché il passaggio da una formula all’altra si basa sulle proprietà di \mu, e non sulle proprietà di \Lambda, la stessa cosa può valere per qualsiasi funzione. Infatti, le Proprietà N.15 e N.16 possono essere sintetizzate in una sola, chiamata formula di inversione di Möbius (anche se, più che di una formula, si tratta di un metodo per ottenere una formula da un’altra):
Formula di inversione di Möbius
Sia n un numero intero positivo. Sia f una qualunque funzione definita su \mathbb{N}^{\star} (non importa l’insieme di arrivo(*)), e sia g la funzione definita per ogni n \in \mathbb{N}^{\star} come segue:
Allora
per ogni n \in \mathbb{N}^{\star}.
(*) Valgono le stesse considerazioni fatte per la Proprietà N.13.
Per dimostrare che
dobbiamo sostituire in quest’uguaglianza la definizione di g, ottenendo:
La tesi segue applicando le Proprietà N.15 e N.16:
Per la Proprietà N.14, la definizione della funzione g si può esprimere anche nella seguente forma, forse più semplice da ricordare: