La media integrale e la funzione di errore assoluto R

Prerequisiti:

• Le funzioni W e V
• Il Teorema di Chebyshev (versione forte)
• Dai numeri interi ai numeri reali – seconda parte

Nell’articolo precedente abbiamo visto che una condizione sufficiente per dimostrare il Teorema dei Numeri Primi è la seguente:

Mentre il nostro punto di partenza, ossia ciò che conosciamo sulla funzione V grazie al Teorema di Chebyshev, è il seguente:

Ci chiedevamo quindi se la (2) implica la (1). Beh, la risposta è sì, ma dimostrarlo non è così semplice come può sembrare. Infatti le equazioni (1) e (2) dicono entrambe qualcosa sulla funzione V, ma in modo molto diverso:

• La (1) esamina un valore puntuale di V, ossia esamina come si comporta V in un singolo punto u (sebbene questo punto non sia fisso, ma variabile per effetto del limite superiore); invece la (2) prende in considerazione l’integrale di V, che è calcolato a partire da più valori della funzione contemporaneamente, in particolare a partire da tutti i valori che si ottengono per 0 \leq u \leq \log x.
• La (1) esamina la funzione V in valore assoluto; la (2) no.

La differenza che riguarda il valore assoluto in realtà è un problema di poco conto, in quanto esso è facilmente inseribile o eliminabile con opportune tecniche algebriche. Ad esempio, nell’articolo precedente lo abbiamo introdotto per ottenere una singola equazione (la (1)) invece di due. Analogamente, a tempo debito potremo introdurlo con tecniche opportune anche nella (2). Per il momento possiamo trascurare questo aspetto ed assumere che il valore assoluto ci sia già, anche se non sappiamo come cambierà la parte destra dell’uguaglianza:

Per il momento l’incognita sulla destra non ha importanza, in quanto il problema fondamentale è un altro: si tratta della prima differenza che abbiamo riscontrato tra la (1) e la (2). Infatti, il valore della funzione |V| in un punto u, dato dalla (1), è un oggetto essenzialmente diverso dall’integrale della stessa funzione su un intervallo, dato dalla (2′), anche se questo intervallo contenesse u. Dal punto di vista grafico, nel primo caso stiamo considerando l’ordinata di un punto del grafico della funzione; nel secondo caso stiamo calcolando l’area sottesa al grafico stesso in un certo intervallo.
Ora, dato che noi dobbiamo dimostrare che la funzione tende a zero, non ci interessano le aree, ma i valori assunti dalla funzione; quindi dobbiamo trovare un modo per trasformare l’integrale in un valore puntuale. Questo modo ci viene fornito da un classico teorema di analisi, il Teorema della media integrale, che per comodità riportiamo qui di seguito:

In altri termini, questo Teorema afferma che l’area sottesa al grafico di un funzione continua f in un intervallo [a, b] è uguale all’area di un rettangolo che ha come base l’ampiezza dell’intervallo, e come altezza un particolare valore assunto dalla funzione nell’intervallo stesso. Tale valore viene chiamato “valor medio di f in [a, b]“, in quanto, se fosse assunto dalla funzione in modo costante su tutto l’intervallo, il valore dell’integrale non cambierebbe; in tal senso, è un valore che compensa i valori più alti e più bassi di esso assunti dalla funzione nell’intervallo, come si può vedere in Figura 1.

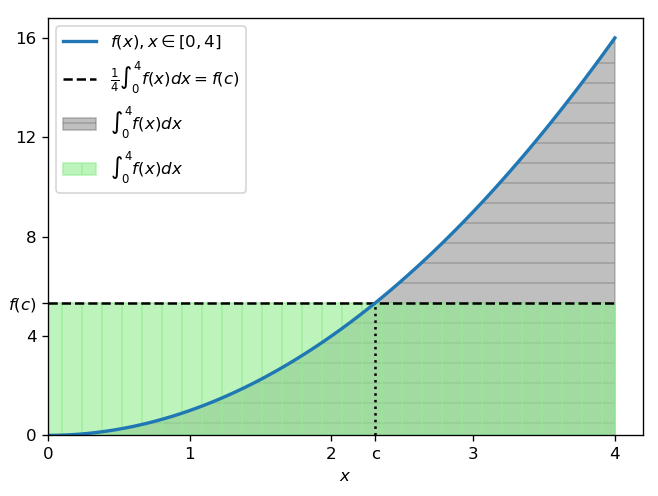
Confrontando la (3) con la (2′), è evidente che, per applicare il Teorema nel nostro caso, dovremmo porre a := 0, b := \log x, x := u ed f := |V|. Peccato però che il Teorema non si possa applicare, perché verrebbe meno un’ipotesi fondamentale: la continuità della funzione. Infatti, come abbiamo visto nell’articolo precedente, la funzione V presenta numerose discontinuità, per cui, essendo x aritrario, non possiamo garantire che non ne presenti nell’intervallo [0, \log x]. Possiamo tuttavia recuperare dal Teorema un’idea fondamentale. Se infatti dividiamo la (3) per b - a otteniamo:

Abbiamo così trasformato l’integrale della funzione f in un valore assunto dalla stessa: è esattamente ciò che volevamo fare per la funzione |V|. Osserviamo che l’espressione che compare a sinistra non dipende dalla continuità di f ma, perché sia definita, è sufficiente che f sia integrabile (ricordiamo che una funzione può essere integrabile ma non continua, come accade per la nostra f che è |V|). Dunque possiamo prendere in prestito dal Teorema l’idea di calcolare questa espressione, che, con le sostituzioni viste prima, diventa nel nostro caso:

Il fatto di non poter applicare il Teorema comporta che questo valore non sia necessariamente uguale al valore assunto dalla funzione in un certo punto c, ma può darsi che questo c non esista, ossia che il valore calcolato dalla (4) non sia effettivamente mai assunto dalla funzione. Questo, però, ci interessa poco: anche se si verificasse questo caso, il valore ottenuto rappresenterebbe comunque una media dei valori della funzione nell’intervallo, pertanto sarebbe comunque confrontabile con essi.

Ora, essendo la (4) una quantità che varia al variare di x, possiamo calcolarne il limite superiore, che chiameremo \beta:

Abbiamo ottenuto così una quantità che è direttamente confrontabile con la parte sinistra della (1), che chiameremo \alpha:

Infatti, come abbiamo detto, l’espressione \frac{1}{\log x} \int_0^{\log x} |V(u)| du che compare nella (5) rappresenta il valor medio della funzione |V| nell’intervallo [0, \log x], e come tale ha senso confrontarlo col valore V(\log x) che compare nella (6), anche se il valor medio non corrispondesse a nessun valore assunto dalla funzione.
Ricapitolando, abbiamo definito due costanti:

Le costanti \alpha e \beta così definite sono dei numeri reali, cioè possiamo escludere che \alpha = +\infty e che \beta = +\infty. Questa proprietà è importante, perché nel seguito della dimostrazione ci servirà usare queste costanti in calcoli algebrici, e discende direttamente dal fatto che la funzione |V| è limitata (Proposizione N.7A):

A questo punto possiamo introdurre la domanda fondamentale della dimostrazione del Teorema dei Numeri Primi: che relazione lega \alpha e \beta? La dimostrazione si giocherà tutta su questa domanda. Infatti, come abbiamo ricordato inizialmente, vogliamo dimostrare la (1), ossia che \alpha = 0. D’altra parte, \beta non può essere negativo, perché, nella (5), non può esserlo |V(u)|, e quindi nemmeno la sua media integrale, e nemmeno il limite superiore della sua media integrale, che è proprio \beta. Quindi sicuramente dovremo dimostrare che \alpha \leq \beta: questo sarà il nostro obiettivo per i prossimi articoli. Esplicitiamolo, partendo dalla (5) e dalla (6):

La prima cosa che potrebbe venire da chiedersi guardando la (7) è se non valga la stessa relazione senza il limite superiore, ossia:

dove il ruolo della x è cambiato: da essere la variabile intera utilizzata per il calcolo del limite superiore, è diventata un intero positivo fissato. Nella (8) quindi lo specifico valore |V(\log x)| viene confrontato con un valor medio calcolato su tutti i precedenti valori della funzione |V|.

Ora non ci resta che fare un po’ di calcoli, per semplificare la formula (9). Infatti, nel membro di sinistra compare l’espressione V(\log x) che si può semplificare facilmente, grazie al fatto che la funzione V è definita attraverso un esponenziale, che si semplifica con il logaritmo:

Potremmo fare dei passaggi analoghi col membro di destra, ma vogliamo fare qualcosa di più raffinato. Il nostro intento non è solo quello di semplificare il logaritmo con l’esponenziale, ma anche quello di passare da un errore relativo, rappresentato dalla funzione W, ad un errore assoluto, rappresentato dal suo numeratore, che d’ora in poi sarà per noi una nuova funzione a sé, chiamata R, il cui grafico è mostrato in Figura 2:

Applicando la Definizione N.15, la (9) si può riscrivere come:

Per semplificare l’integrale a destra nella (8) sono invece necessari passaggi più complessi, al termine dei quali si ottiene:

Sostituendo la (11) e la (12) nella (8), abbiamo che:

Notiamo nell’ultimo passaggio la semplificazione di \frac{1}{x}, che finalmente toglie il denominatore da \frac{R(x)}{x}, facendoci passare così da un errore relativo ad un errore assoluto (per chi ha letto la parte di dettaglio, questo passaggio è il motivo per cui nell’integrale abbiamo utilizzato la sostituzione t := \frac{x}{e^u} invece della più semplice t := e^u).

Abbiamo così ottenuto il seguente Lemma:

Ricapitolando, possiamo formulare la seguente Ipotesi:

Per studiare l’Ipotesi N.1 dobbiamo quindi trovare una relazione che leghi \log x |R(x)| e \int_1^x |R(\frac{x}{t})| dt. Per cominciare, possiamo semplificare sostituendo l’integrale con una sommatoria, introducendo nel contempo dei coefficienti a_n da scegliere opportunamente al fine di ottenere una quantità simile all’integrale: \sum_{n = 1}^x a_n |R(\frac{x}{n})| (si tratta di un’evoluzione dell’approccio che abbiamo visto qui: Dai numeri interi ai numeri reali: seconda parte). Selberg, il matematico di cui abbiamo parlato nell’articolo Il Teorema dei Numeri Primi: storia ed enunciato, ha scoperto una relazione asintotica tra il termine col logaritmo e una sommatoria di questo tipo, entrambi però senza il valore assoluto. Chiameremo questa relazione Teorema di Selberg:

Ma come si giustifica la scelta del coefficiente a_n := \Lambda(n)? Per capirlo, dobbiamo prima aprire una lunga parentesi, che ci impegnerà per i prossimi tre articoli, nei quali ci dimenticheremo dei passaggi della dimostrazione che abbiamo fatto finora; poi torneremo sui nostri passi e vedremo come si arriva al Teorema di Selberg e come viene applicato per la dimostrazione del Teorema dei Numeri Primi.