Prerequisiti:
- Il Teorema dei Numeri Primi: storia ed enunciato
- Il Teorema di Chebyshev (versione forte)
- Dai numeri interi ai numeri reali
- Il Teorema di Chebyshev (versione debole)
Nell’articolo precedente abbiamo visto che l’unica differenza tra l’enunciato della versione forte del Teorema di Chebyshev e quello del Teorema dei Numeri Primi, è che il primo non stabilisce l’esistenza del limite
mentre il secondo sì. Non a caso, infatti, l’idea generale della dimostrazione del Teorema dei Numeri Primi consiste nel partire dalla dimostrazione del Teorema di Chebyshev (versione forte), riutilizzandone le parti salienti al fine di dimostrare la parte mancante, ossia l’esistenza del limite (1). Possiamo quindi vedere il Teorema di Chebyshev come una tappa intermedia, una fonte di ispirazione per arrivare al Teorema dei Numeri Primi.
Rileggendo l’articolo sulla versione forte del Teorema di Chebyshev, possiamo osservare che il passaggio chiave — quello che ci ha permesso di dire che il limite (1), se esiste, è 1 — è la seguente equazione:
Questo sarà il nostro punto di partenza. Il nostro obiettivo sarà capire qualcosa in più sulla funzione \psi (e sulla sua estensione semplice \overline{\psi}), fino a dimostrare che
Infatti, se dimostrassimo questo, potremmo arrivare al Teorema dei Numeri Primi in un solo passaggio, dato che, per il Corollario del Teorema N.5 (Equivalenza asintotica tra \pi(x) e \frac{\psi(x)}{\log x}), \pi(x) \sim \frac{\psi(x)}{\log x}, e dunque per transitività avremmo:
Ora che abbiamo chiari il punto di partenza e l’obiettivo, possiamo cominciare con la dimostrazione vera e propria. Sarà lunga e complessa, ma cercheremo di evidenziare i passaggi chiave, per non perdere il filo del discorso. Per ora dobbiamo ricordare le formule (2) e (3′) che sono rispettivamente quella iniziale e quella finale; nei prossimi articoli vedremo quali altre formule importanti ci sono nel mezzo.
Il primo passaggio della dimostrazione, oggetto di questo articolo, è un artificio tecnico: si tratta di riscrivere la (2) in una forma più semplice, eliminando il quadrato al denominatore ed il logaritmo. Mediante opportuni passaggi si può infatti arrivare alla forma seguente:
Partendo dalla formula (2), per prima cosa osserviamo che \log x = \int_1^x \frac{1}{t} dt; infatti, svolgendo questo integrale, si ottiene che \int_1^x \frac{1}{t} dt = [\log t]_1^x = \log x - \log 1 = \log x - 0 = \log x. Riscrivendo il logaritmo in questo modo ed utilizzando le proprietà della somma algebrica degli integrali, si ottiene:
A questo punto, per eliminare il fattore \frac{1}{t} all’interno dell’integrale, è possibile utilizzare la sostituzione t := e^u, da cui dt = e^u du. Per effetto di questa sostituzione, gli estremi di integrazione cambiano, in quanto, se t = 1, allora e^u = 1, e quindi u = 0, che diventa così il nuovo estremo inferiore; analogamente, se t = x allora e^u = x e quindi u = \log x, che diventa il nuovo estremo superiore. Con queste sostituzioni, si ottiene la formula (4):
La funzione integranda ha una struttura molto semplice, essendo esprimibile come composizione della funzione \frac{\overline{\psi}(t) - t}{t}, con la funzione esponenziale. D’ora in poi chiameremo la funzione integranda V e la sua prima funzione componente W:
Funzioni W e V
Si definiscono le seguenti funzioni W: [1, +\infty) \rightarrow \mathbb{R} e V: \mathbb{R}_{+} \rightarrow \mathbb{R}:
Dalla Definizione N.13 segue immediatamente che
per ogni u \in \mathbb{R}^{+}.
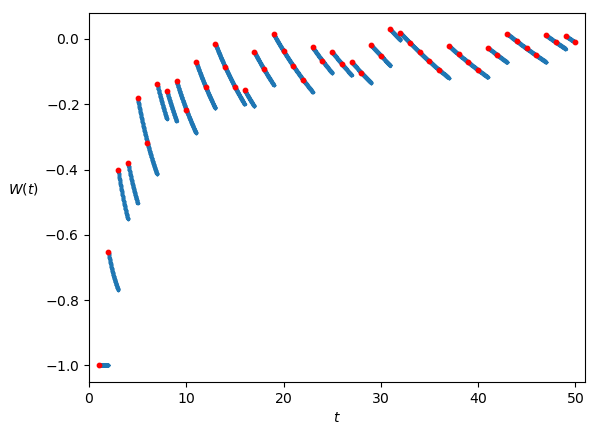
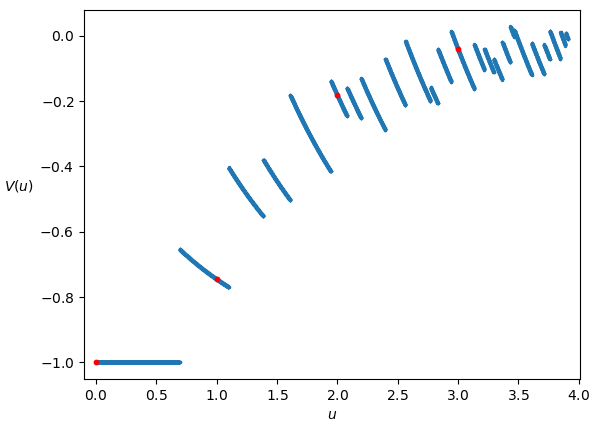
I grafici delle funzioni W e V sono mostrati rispettivamente nelle Figure 1 e 2.
Nella parte finale della dimostrazione studieremo questi grafici in modo approfondito; per il momento invece ci limitiamo ad osservare alcune semplici cose:
- Il grafico della funzione W presenta delle discontinuità in corrispondenza degli interi per i quali la funzione \overline{\psi} cambia valore. Ad esempio, per t=1, \ldots, 6 si ha che \overline{\psi}(t) = \psi(t) = \log 1, \log 2, \log 6, \log 12, \log 60, \log 60, dunque \overline{\psi} cambia valore nel passaggio da 1 a 2, da 2 a 3, da 3 a 4, da 4 a 5, ma resta costante passando da 5 a 6. Nel grafico (Figura 1), questo è evidenziato dal fatto che vi sono discontinuità nei punti 2, 3, 4, e 5, ma non nel punto 6. Infatti i punti 5 e 6 si trovano graficamente su uno stesso tratto di linea continua.
- A partire da un intero fino a prima del successivo, la funzione W è strettamente decrescente.
- Il grafico della funzione V tra due interi n ed n + 1 riproduce il grafico della funzione W tra e^n ed e^{n + 1}. La Figura 3 fa vedere questo per n = 1.
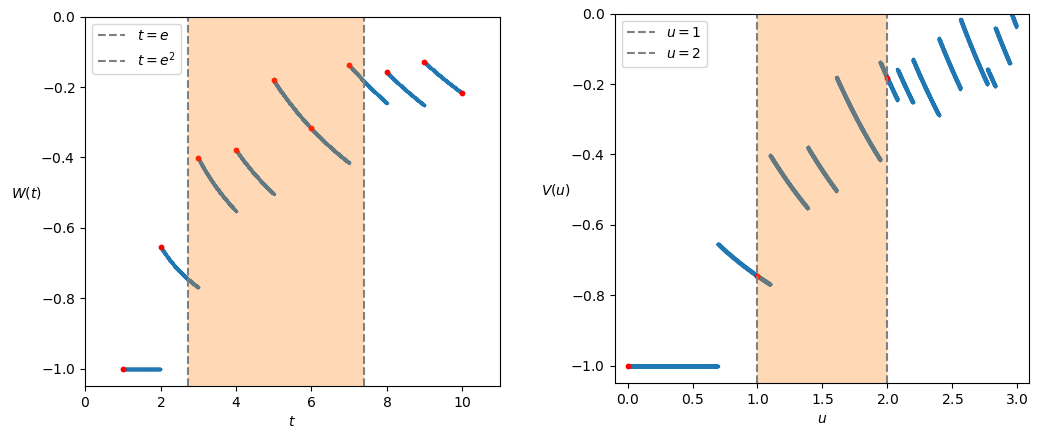
I primi due punti, in particolare, sono una base di partenza per la dimostrazione della seguente Proposizione:
Le funzioni |W| e |V| sono limitate
Le funzioni |W| e |V| sono limitate.
Osserviamo che, per la Definizione N.13:
Quindi, per dimostrare che |W| è limitata, bisogna dimostrare che la funzione \left| \frac{\overline{\psi}(t)}{t} \right| è limitata. Possiamo osservare che questa funzione è uguale a \frac{\overline{\psi}(t)}{t}: il valore assoluto può essere eliminato, perché sia \overline{\psi}(t) che t sono non negativi; quindi dobbiamo dimostrare che la funzione \frac{\overline{\psi}(t)}{t} è limitata.
Innanzitutto, per valori interi di t vale il Teorema N.4, per il quale \psi(t) \asymp t. Per la Definizione A.3, ciò significa che esiste una costante reale positiva A tale che definitivamente |\psi(t)| \leq At, da cui, essendo \psi non negativa, \psi(t) \leq At, cioè \frac{\psi(t)}{t} \leq A. Ma, sempre limitandoci ai valori interi di t, se l’ultima disuguaglianza è vera definitivamente, cioè per ogni t maggiore o uguale a un certo t_0, allora una disuguaglianza analoga è anche vera per ogni t. Infatti, l’insieme dei valori \left\{\frac{\psi(1)}{1}, \frac{\psi(2)}{2}, \ldots, \frac{\psi(t_0 - 1)}{t_0 - 1}\right\}, essendo finito, ammette un valore massimo M, quindi per t \lt t_0 si ha che \frac{\psi(t)}{t} \leq M, e quindi in generale, considerando anche il caso di t \geq t_0, si ha che \frac{\psi(t)}{t} \leq \max(M, A). Quindi la funzione \frac{\psi(t)}{t}, per valori interi di t (vincolo che la fa coincidere con la funzione \frac{\overline{\psi}(t)}{t}), è limitata.
Vediamo ora cosa succede per valori non interi di t. In particolare, concentriamoci sugli intervalli del tipo (n, n+1), dove n è un intero positivo. In questi intervalli, per definizione di estensione semplice, la funzione \overline{\psi} è costante e pari a \psi(n), quindi per t \in (n, n+1) si ha che \frac{\overline{\psi}(t)}{t} = \frac{\psi(n)}{t} \lt \frac{\psi(n)}{n}. Ma, per la parte precedente, \frac{\psi(n)}{n} \leq \max(M, A), quindi la disuguaglianza \frac{\overline{\psi}(t)}{t} \leq \max(M, A) vale in tutti gli intervalli del tipo (n, n+1) e, includendo n, anche in tutti gli intervalli del tipo [n, n+1). Ma, per n \geq 1, l’unione di questi intervalli ricopre tutto il dominio della funzione, che è lo stesso di W e cioè [1, +\infty), quindi possiamo dire che \frac{\overline{\psi}(t)}{t} \leq \max(M, A) per ogni t. Quindi la funzione \frac{\overline{\psi}(t)}{t} è limitata, che è quello che volevamo dimostrare.
La limitatezza della funzione |V| a questo punto è un’immediata conseguenza, dato che |V(u)| = |W(e^u)| \leq \max(M, A), per ogni u.
La Definizione N.13 consente di riscrivere la (4) come:
Ora analizziamo più a fondo le funzioni W e V.
La funzione W calcola un errore relativo. Infatti il numeratore \overline{\psi}(t) - t è un’estensione della funzione \psi(x) - x, che rappresenta la differenza tra la quantità che dobbiamo stimare e la stima asintotica che vogliamo ottenere, per la (3). La funzione W tuttavia non esprime questa differenza in assoluto, ma relativamente al valore della x (che con l’estensione ai reali diventa t). Questo è un principio generale di quando si calcola un errore relativo: ad esempio, una cosa è sbagliare di un’unità su un migliaio, un’altra cosa è sbagliare di un’unità su un milione, dato che l’errore relativo è di un millesimo nel primo caso, mentre è di un milionesimo nel secondo.
L’errore relativo è quindi una funzione che indica in modo abbastanza intuitivo la somiglianza tra due valori, in questo caso \psi(x) e x. Per la (3), dobbiamo dimostrare che c’è una certa somiglianza tra queste due funzioni (ossia che c’è equivalenza asintotica) e quindi, intuitivamente, possiamo aspettarci che l’errore relativo W(x) = \frac{\overline{\psi}(x) - x}{x} = \frac{\psi(x) - x}{x} tenda a zero. In effetti, le due cose sono equivalenti:
Quindi abbiamo ulteriormente riformulato il nostro obiettivo, che dalla formula (3) può essere riscritto equivalentemente come:
Ma, per la Definizione N.13, W(x) = W(\exp(\log x)) = V(\log x), per cui:
Abbiamo ottenuto così un’ulteriore riformulazione del nostro obiettivo:
Ricapitolando, abbiamo la seguente catena di implicazioni (che sono in realtà delle doppie implicazioni) che ci portano verso il Teorema dei Numeri Primi:
Abbiamo così ricondotto la dimostrazione del Teorema dei Numeri Primi al problema di dimostrare che \lim_{x \to +\infty} V(\log x) = 0. Attenzione, perché in questa scrittura è sottinteso che il limite esiste, oltre a essere 0; l’esistenza del limite è sempre parte della tesi da dimostrare. Come dimostrare dunque che il limite di una funzione esiste ed è 0?
Il metodo più immediato è applicare la Proposizione A.2 (Ogni successione reale avente \liminf e \limsup uguali ammette limite), secondo la quale:
Cioè, per dimostrare che il limite di V esiste ed è 0, bisognerebbe dimostrare che il limite superiore ed il limite inferiore della funzione sono anch’essi pari a zero. Il vantaggio di questa tecnica è che il limite superiore ed il limite inferiore, a differenza del limite, per definizione esistono sempre; vanno solo calcolati (ammettendo come valori possibili anche \pm \infty). Quindi la (5) permette di stabilire il valore numerico e l’esistenza di un solo oggetto (il limite della funzione V) sulla base del valore numerico di due oggetti distinti (il suo limite superiore ed inferiore), dei quali però non dobbiamo preoccuparci dell’esistenza. Tutto sommato è una buona semplificazione. Lo svantaggio è che ora abbiamo due equazioni che bisognerebbe dimostrare separatamente: \limsup_{x \to +\infty} V(\log x) = 0 e \liminf_{x \to +\infty} V(\log x) = 0. In linea di principio, dimostrata una delle due, bisognerebbe ricominciare tutta la dimostrazione da capo per dimostrare anche l’altra. Anche qui, però, è possibile semplificare, riunendo le due equazioni in una sola. Infatti, si dimostra che:
In questo dettaglio indicheremo per brevità \limsup_{x \to +\infty} V(\log x) e \liminf_{x \to +\infty} V(\log x) semplicemente come \limsup V e \liminf V. Cominciamo a dimostrare l’implicazione verso destra: \limsup V = \liminf V = 0 \Rightarrow \limsup |V| = 0.
Riprendendo la formula (5), abbiamo che, se \limsup V = \liminf V = 0, allora la funzione V tende a zero. Ma se V tende a zero, anche la sua opposta -V tende a zero (per definizione di limite, oppure perché \lim -V = -\lim V = -0 = 0), quindi anche il suo valore assoluto tende a zero, per il cosiddetto “Teorema dei carabinieri“, essendo -V \leq |V| \leq V. In sintesi, 0 = \lim V = \lim -V = \lim |V|. Ma se \lim |V| = 0, allora, per la già citata Proposizione A.2, \limsup |V| = \liminf |V| = 0; in particolare \limsup |V| = 0, che è ciò che volevamo dimostrare.
Viceversa, se \limsup |V| = 0, essendo V \leq |V|, per definizione di limite superiore (e come è anche facile intuire), si ha che \limsup V \leq \limsup |V|, per cui:
Possiamo osservare che, essendo |V| = |-V|, possiamo sostituire -V al posto di V in tutti i passaggi precedenti, fino alla fomula (7), ottenendo:
Ora possiamo sfruttare una proprietà generale che lega il limite superiore e quello inferiore, che nel nostro caso si traduce nell’uguaglianza \limsup -V = -\liminf V, da cui, per la (7′), -\liminf V \leq 0, ossia:
Mettendo insieme la (7) e la (8), si ottiene che \limsup V \leq 0 \leq \liminf V, dunque \limsup V \leq \liminf V. Ma sappiamo che in generale vale sempre la relazione inversa, ossia che \liminf V \leq \limsup V; per cui in questo caso, essendo vere entrambe le relazioni, si deve avere che \liminf V = \limsup V. Inoltre, sempre per la (7) e per la (8), possiamo estendere questa disuguaglianza, ottenendo 0 \leq \liminf V = \limsup V \leq 0, e quindi \liminf V = \limsup V = 0, che è quello che dovevamo dimostrare.
Quindi, a patto di introdurre il valore assoluto, è possibile tornare ad una sola equazione, come quando avevamo il limite, mantenendo tuttavia il vantaggio del \limsup, che è quello di esistere sempre. Certo, il valore assoluto non è un oggetto così facile da trattare, ma potremo sviluppare gran parte della dimostrazione senza di esso, per poi aggiungerlo solo quando necessario.
A questo punto, dato che abbiamo fatto vari passi all’indietro per ottenere formule via via più semplici, è utile fermarsi un attimo per ricapitolare il tutto, ripercorrendo in avanti i passaggi. Per quanto riguarda il nostro obiettivo, per arrivare alla formula del Teorema dei Numeri Primi abbiamo percorso la seguente catena di implicazioni (alcune delle quali sono doppie implicazioni, ma ciò non ha importanza ai fini della dimostrazione):
Questa catena di implicazioni dimostra il seguente Lemma, in base al quale nei prossimi articoli potremo dimenticarci dei passaggi di cui sopra e concentrarci sulla dimostrazione della formula \limsup_{x \to +\infty} |V(\log x)| = 0:
Condizione sufficiente per la validità del Teorema dei Numeri Primi
Una condizione sufficiente per la validità del Teorema dei Numeri Primi è la seguente:
dove la funzione V è definita nella Definizione N.13.
Anche il nostro punto di partenza è stato oggetto di alcuni passaggi a ritroso, che ci hanno permesso di introdurre la funzione V e si possono riassumere come segue:
Quindi, sostanzialmente, se dimostrassimo l’implicazione:
avremmo dimostrato il Teorema dei Numeri Primi. Infatti, i passaggi precedenti e la formula (2) garantiscono che la parte sinistra è vera, mentre il Lemma N.7 garantisce la sufficienza della parte destra; ciò che manca è dimostrare l’implicazione.
Nel prossimo articolo vedremo come, partendo dalla (9), sia possibile impostare il seguito della dimostrazione.