Prerequisiti:
In teoria dei numeri, molte dimostrazioni sono di tipo “tecnico”, ossia consistono principalmente in una serie di passaggi di tipo algebrico, mediante i quali un’espressione iniziale viene ridotta in forme via via più semplici, fino a ricondurla a qualcosa di già noto. In questo articolo vedremo un paio di dimostrazioni di questo tipo, che ci daranno l’occasione di apprendere alcune tecniche riutilizzabili in altri contesti.
Dimostreremo i seguenti lemmi:
Primo lemma sulle sommatorie con la funzione di Möbius e il logaritmo
dove la funzione sulla sinistra si intende definita per x \in \mathbb{N}^{\star}.
Secondo lemma sulle sommatorie con la funzione di Möbius e il logaritmo
dove la funzione sulla sinistra si intende definita per x \in \mathbb{N}^{\star}.
Se si segue il percorso sulla dimostrazione “elementare” del Teorema dei Numeri Primi, nel prossimo articolo si vedrà che il secondo Lemma sarà utilizzato per dimostrare il Teorema di Selberg, e si vedrà da dove esso ha origine. Indipendentemente da ciò, però, entrambi i Lemmi possono essere utili per apprendere alcune tecniche di teoria dei numeri.
Dal punto di vista pratico, la funzione del Lemma N.9 sembra molto ben approssimata dalla funzione identità, tanto che le due funzioni sembrano essere asintoticamente equivalenti:
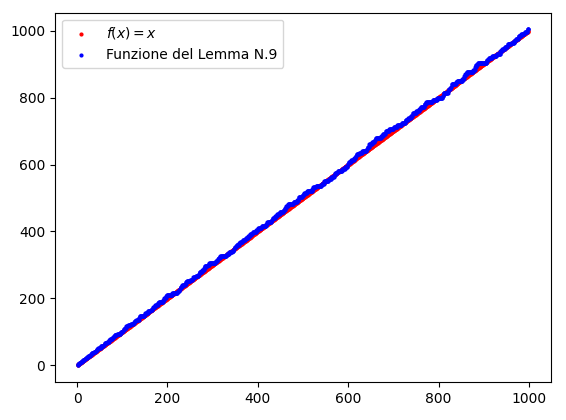
La funzione del Lemma N.10 è invece approssimata dalla funzione 2x \log x in modo abbastanza grossolano:
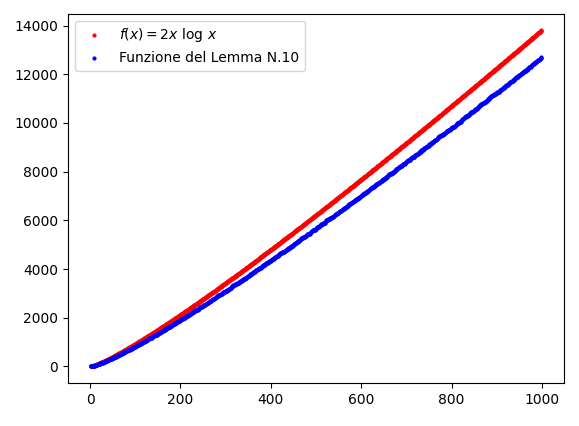
In effetti, secondo il Lemma N.10, approssimando la funzione \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left(\frac{x}{d}\right) con 2x \log x si commette un errore O(x). Empiricamente, però, possiamo stimare questo errore come -x, ottenendo un’approssimazione decisamente migliore:
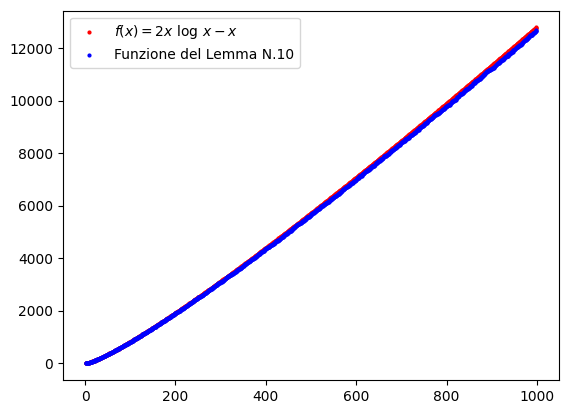
Quest’evidenza ci induce a pensare che in realtà valga il risultato più forte \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left(\frac{x}{d}\right) = 2x \log x - x + o(x). Se qualcuno dei nostri lettori riesce a dimostrare la verità o la falsità di questa affermazione, può contattarci.
Dimostrazione del primo lemma
Cominciamo a semplificare l’espressione del primo lemma:
Possiamo osservare che in generale ogni d della sommatoria interna divide più n della sommatoria esterna. Ad esempio, se x = 8 allora il numero d = 2 divide n, con 1 \leq n \leq x, per n \in \{2, 4, 6, 8\}; quindi il termine \mu(2) \log^2 \left(\frac{8}{2}\right) comparirà quattro volte, una volta espanse entrambe le sommatorie. Così, contando quante volte compare ciascun termine, possiamo ridurre la doppia sommatoria ad una sommatoria singola. Vale infatti la seguente Proprietà generale:
Semplificazione della doppia sommatoria per n \leq x e per d \mid n
Sia x un intero positivo. Sia f una qualunque funzione definita sui numeri interi positivi (non importa l’insieme di arrivo(*)). Allora:
(*) Per la precisione, è necessario che sull’insieme di arrivo sia definita l’operazione di somma, e che essa sia commutativa. Tuttavia in questo contesto è inutile porsi il problema, perché ciò è vero per gli insiemi numerici che ci interessano (\mathbb{N}, \mathbb{Z} ed \mathbb{R}).
Per rendere più intuitiva la dimostrazione, possiamo costruire una tabella di x righe e altrettante colonne, numerate a partire da 1, dove nella cella di riga r e colonna c inseriamo il valore di f(r) se e solo se r \mid c. Ad esempio, per x = 10 si avrebbe la seguente tabella:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | f(1) | f(1) | f(1) | f(1) | f(1) | f(1) | f(1) | f(1) | f(1) | f(1) |
| 2 | f(2) | f(2) | f(2) | f(2) | f(2) | |||||
| 3 | f(3) | f(3) | f(3) | |||||||
| 4 | f(4) | f(4) | ||||||||
| 5 | f(5) | f(5) | ||||||||
| 6 | f(6) | |||||||||
| 7 | f(7) | |||||||||
| 8 | f(8) | |||||||||
| 9 | f(9) | |||||||||
| 10 | f(10) |
Se leggiamo questa tabella per colonne, in ciascuna colonna n troveremo il valore f(d) per tutti e soli i divisori d di n. Quindi la somma della colonna n è \sum_{d \mid n} f(d), e la somma di tutta la tabella è:
Proviamo ora a leggere la stessa tabella per righe.
Per ciascuna riga n, il valore di f(n) è ripetuto tante volte quanti sono i multipli di n minori o uguali di 10, ossia \left \lfloor \frac{10}{n} \right \rfloor volte, per la Proprietà N.5. Quindi la somma della riga n è \left \lfloor \frac{10}{n} \right \rfloor f(n), e la somma di tutta la tabella è:
Ma, trattandosi della stessa tabella di prima, le somme (a) e (b) devono coincidere, per cui:
Si può osservare che la variabile n rappresenta nella sommatoria di sinistra il numero di colonna, mentre nella sommatoria di destra il numero di riga. Trattandosi di due sommatorie diverse, però, non c’è problema ad utilizzare lo stesso simbolo con un diverso significato. Anzi, l’uso dello stesso simbolo evidenzia il fatto che si tratta della medesima operazione, ossia la sommatoria estesa a tutti gli interi positivi minori o uguali ad x, al di là di ciò che questi interi rappresentano.
Chiaramente il ragionamento fatto fin qui per x = 10 può estendersi a qualunque valore di x (che, ricordiamo, deve essere un numero intero positivo), per cui si ottiene la tesi.
È importante osservare che la Proprietà N.19 non implica che, per ogni n \leq x, \sum_{d \mid n} f(d) = \left \lfloor \frac{x}{n} \right \rfloor f(n). Infatti non potrebbe essere così, perché al crescere di x la parte destra di quest’ultima uguaglianza è crescente, mentre la parte sinistra resta costante. L’uguaglianza delle sommatorie \sum_{n \leq x} \sum_{d \mid n} f(d) e \sum_{n \leq x} \left \lfloor \frac{x}{n} \right \rfloor f(n) vale quindi globalmente, non termine a termine.
Applicando la Proprietà N.19 alla formula (1), si ottiene:
Cerchiamo ora di stimare il membro di destra. Come spesso si fa in teoria dei numeri, quando ci sono delle parti intere, esse possono essere semplicemente tolte, stimando poi l’errore così introdotto. Nel nostro caso si ottiene:
dove abbiamo chiamato \mathrm{Err}(x) l’errore, pari a - \sum_{n \leq x} \left( \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right) \mu(n) \log \left(\frac{x}{n}\right). Troviamo una maggiorazione di quest’errore in valore assoluto:
dove nel penultimo passaggio abbiamo considerato che x \leq n \Rightarrow \frac{x}{n} \geq 1 \Rightarrow \log \left(\frac{x}{n}\right) \geq 0; inoltre, nell’ultimo passaggio, abbiamo usato il fatto che \left| \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right| \leq 1 e |\mu(n)| \leq 1, per cui \left| \left( \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right) \mu(n)\right| = \left| \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right| |\mu(n)| \leq 1.
Ci siamo ricondotti così alla sommatoria \sum_{n \leq x} \log \left(\frac{x}{n}\right), che conosciamo già: infatti, per il Lemma N.6 (Funzione somma dei logaritmi di una frazione al variare del denominatore)
:
Ora, unendo le formule (2)-(5), abbiamo che:
Resta quindi da stimare la sommatoria \sum_{n \leq x} \frac{\mu(n)}{n} \log \left(\frac{x}{n}\right). Questa sommatoria non è immediatamente riconducibile a quelle che già conosciamo (ad esempio quella della Proprietà N.12, forma logaritmica (Espressione di \Lambda mediante \mu), perciò per stimarla è necessario qualche artificio tecnico.
Il trucco principale è utilizzare il Teorema N.6 (Approssimazione della somma degli inversi dei primi numeri interi). Per questo Teorema:
Il Teorema N.6 non è direttamente applicabile per calcolare \log \left(\frac{x}{n}\right), perché \frac{x}{n} può non essere un numero intero. Tuttavia, possiamo facilmente ricondurci al caso di un numero intero, ricordando che il logaritmo è una funzione crescente, per cui, essendo \left\lfloor \frac{x}{n}\right\rfloor \leq \frac{x}{n} \leq \left\lfloor \frac{x}{n}\right\rfloor + 1:
Applicando il Teorema N.6, abbiamo che:
Osserviamo che
dove nei passaggi centrali abbiamo applicato le proprietà degli ordini asintotici A.5 e A.8. Sostituendo nella (a), abbiamo:
che a sua volta è equivalente a:
Ora osserviamo che:
Quindi dalla (b) si può ottenere, per la Proprietà A.15:
da cui, per la Proprietà A.13:
che equivale alla (7).
In alternativa, si potrebbe dimostrare una versione estesa del Teorema N.6, valida per i numeri reali. L’enunciato e la relativa dimostrazione sarebbero solo leggermente diversi da quelli visti nell’articolo La somma degli inversi dei primi numeri interi positivi.
Ora potremmo effettuare la sostituzione (7) all’interno della (6), riscrivendo la sommatoria sulla destra come segue:
Mediante alcune trasformazioni algebriche, si può dimostrare che la prima sommatoria è pari ad 1:
Per semplificare questa sommatoria, si può usare la Proprietà N.20.
Per prima cosa possiamo riscrivere la sommatoria come segue:
dove nel secondo passaggio abbiamo applicato la Proprietà N.20 con a := n, b := k, n := x e f(a, b) := \frac{\mu(a)}{ab}.
Ora trasformiamo ulteriormente la sommatoria:
dove nella seconda uguaglianza abbiamo applicato la Proprietà N.14.
Ora, per la Proprietà N.11, \sum_{d \mid m} \mu(d) è 1 se m = 1 e 0 altrimenti, per cui:
La (9) si ottiene quindi unendo le formule (c), (d) ed (e).
La terza sommatoria della (8) invece è facilmente stimabile come O(1):
Applicando la proprietà degli ordini asintotici Corollario 1 della Proprietà A.8, possiamo semplificare la sommatoria come segue:
L’ultima sommatoria si può maggiorare in valore assoluto come segue:
Quindi, per la proprietà degli ordini asintotici Proprietà A.12, \sum_{n \leq x} \mu(n) = O(x). Infine, sostituendo nella (f) e applicando la Proprietà A.8, abbiamo che:
Unendo le formule (f) e (g), si ottiene la (10).
La seconda sommatoria invece, \sum_{n \leq x} \frac{\mu(n)}{n}, è difficile da stimare o da semplificare, tanto che siamo costretti a cambiare strategia per eliminarla. Osserviamo che questa sommatoria, nella (8), è moltiplicata per \gamma: l’idea consiste quindi nell’eliminare \gamma, in modo che si elimini anche la sommatoria che la moltiplica. Questo si può fare aggiungendo e sottraendo \gamma al primo membro della (6):
dove, nell’ultimo passaggio, si è utilizzato il fatto che \sum_{d \mid n} \mu(d), per la Proprietà N.11, vale 1 se n = 1 e 0 altrimenti. Ora, per la (7), \log \left(\frac{x}{d}\right) + \gamma = \sum_{k \leq \left\lfloor \frac{x}{n} \right\rfloor} \frac{1}{k} + O\left( \frac{n}{x} \right); effettuando questa sostituzione, in un solo colpo spariscono dall’interno della sommatoria sia il logaritmo che la costante \gamma. Prima di procedere con la sostituzione, però, il logaritmo ci serve per semplificare la sommatoria. Infatti, i passaggi (2)-(5) si possono ripetere con \log \left(\frac{x}{d}\right) + \gamma al posto di \log \left(\frac{x}{d}\right), ottenendo alla fine:
Procedendo come per le formule (2) e (3), mettendo \log \left(\frac{x}{n}\right) + \gamma al posto di \log \left(\frac{x}{n}\right), si ottiene:
dove \mathrm{Err'}(x) := - \sum_{n \leq x} \left( \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right) \mu(n) \left( \log \left(\frac{x}{n}\right) + \gamma \right ). Ora,
Ma, riprendendo il discorso della formula (4), \left | \sum_{n \leq x} \left( \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right) \mu(n) \right | \leq \sum_{n \leq x} \left | \left( \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right) \mu(n) \right | \leq \sum_{n \leq x} 1 = x; quindi, per la Proprietà A.12, \sum_{n \leq x} \left( \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right) \mu(n) = O(x). Allora, applicando il Corollario 2 e il Corollario 3 della Proprietà A.8, e il Corollario della Proprietà A.9:
Unendo le formule (3′), (h) ed (i), si ottiene la (6′).
Ora possiamo effettuare la sostituzione data dalla (7) e semplificare, applicando le proprietà degli ordini asintotici Corollario della Proprietà A.7 e Corollario della Proprietà A.9:
Per concludere, mettendo insieme le formule (11), (6′) e (12) e applicando le proprietà degli ordini asintotici Corollario 3 della Proprietà A.8, Corollario della Proprietà A.7, Proprietà A.11 e Corollario della Proprietà A.9, abbiamo che:
Così il Lemma N.9 è dimostrato.
Dimostrazione del secondo lemma
Il secondo lemma si dimostra in modo molto simile al primo, ma i calcoli sono un po’ più complessi, per la presenza del quadrato del logaritmo. Come per il lemma precedente, conviene sostituire il logaritmo per mezzo della (7), facendo in modo però che la costante \gamma resti fuori dalle sommatorie. Come per la (11), dobbiamo cercare di ottenere il termine \log \left(\frac{x}{d}\right) + \gamma. In questo caso, essendoci il quadrato del logaritmo, si può fare in questo modo:
Ora possiamo ottenere il termine \log \left(\frac{x}{d}\right) + \gamma, scomponendo la differenza di quadrati \log^2 \left(\frac{x}{d}\right) - \gamma^2 come \left( \log \left(\frac{x}{d}\right) - \gamma \right)\left( \log \left(\frac{x}{d}\right) + \gamma \right). Prima di fare questo, però, semplifichiamo la sommatoria come abbiamo fatto nella (6′):
Procedendo come per le formule (2) e (3), mettendo \log^2 \left(\frac{x}{n}\right) - \gamma^2 al posto di \log \left(\frac{x}{n}\right), si ottiene:
dove \mathrm{Err''}(x) := - \sum_{n \leq x} \left( \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right) \mu(n) \left( \log^2 \left(\frac{x}{n}\right) - \gamma^2 \right ). Ora,
Procedendo come per la (4), si ottiene che:
Ma la sommatoria di destra è O(x), per il Lemma N.6A (Funzione somma dei logaritmi di una frazione al variare del denominatore, forma generalizzata), quindi per la Proprietà A.12:
Concludendo, la (6”) segue dalle formule (3”), (j) e (k).
Ora, applicando la (7), possiamo scomporre la sommatoria di destra come segue:
La prima sommatoria è una versione più complicata della (9). Facendo un po’ di conti ed applicando alcune proprietà della funzione di Möbius e della funzione \Lambda, si dimostra che:
Procedendo come per la (9), si dimostra che:
Anche in questo caso, come abbiamo fatto per la formula (e), conviene distinguere i casi m = 1 e 2 \leq m \leq x:
Per le Proprietà N.11 e N.12 (forma logaritmica), quest’ultima espressione è uguale a:
Per stimare la sommatoria possiamo applicare il Corollario della Proposizione N.7, come segue:
Quindi, unendo le formule (m), (n) ed (o) ed applicando il Corollario della Proprietà A.7, si ottiene:
da cui, per la (l), si ottiene la (9′).
La seconda sommatoria della (13) è molto simile alla (10), infatti si dimostra che vale la stessa stima asintotica:
Procedendo come per la (10), si dimostra che:
Quest’ultima sommatoria, applicando le proprietà degli ordini asintotici Corollario della Proprietà A.7, Proprietà A.5 e Corollario della Proprietà A.9, si può stimare come segue:
dove, nel penultimo passaggio, abbiamo applicato nuovamente il Lemma N.6.
Quindi, per la Proprietà A.12, \sum_{n \leq x} \mu(n) \left( \log \left(\frac{x}{n}\right) - \gamma \right) = O(x): sostituendo questo nella (p) si ottiene la (10′).
La dimostrazione si conclude mettendo insieme le formule precedenti ed applicando le stesse proprietà degli ordini asintotici già applicate in precedenza: