Prerequisiti:
In questo articolo vedremo due concetti di analisi matematica che ci serviranno in teoria dei numeri: il limite inferiore (\lim \inf) ed il limite superiore (\lim \sup) di una successione.
Come nell’articolo sull’analisi asintotica, non abbiamo la pretesa di trattare l’argomento del dettaglio, ma il nostro intento è piuttosto quello di dare un’idea intuitiva di cosa siano il limite superiore ed il limite inferiore di una successione, senza però trascurare il rigore matematico.
Successioni ed intervalli
Consideriamo una successione reale (a_n)_{n \geq 0} = a_0, a_1, a_2, \ldots, a_n, \ldots, cioè una successione dove tutti gli a_n sono numeri reali. Essendo essa di fatto una funzione da \mathbb{N} in \mathbb{R} che associa n ad a_n, possiamo rappresentarla sul piano cartesiano rappresentando n sull’asse orizzontale ed a_n sull’asse verticale, come in Figura 1.
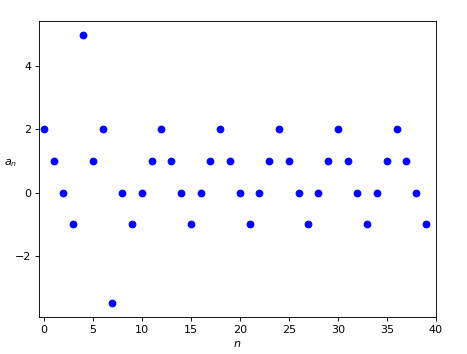
La successione mostrata in Figura 1 è data dalla seguente definizione matematica:
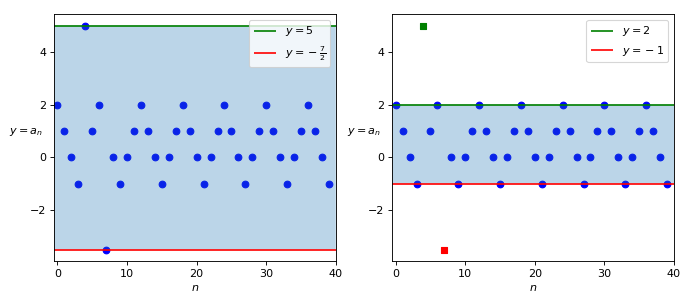
Al di là della formulazione algebrica dell’ultimo caso, che in questo contesto ha poca importanza, è evidente che i casi n = 4 ed n = 7 sono gestiti come eccezioni; dunque possiamo immaginare che, proseguendo all’infinito verso destra, il grafico continui sempre con lo stesso andamento, oscillando tra i valori -1 e 2. Possiamo individuare quindi due intervalli sull’asse verticale, ai quali corrispondono due fasce orizzontali nel grafico (Figura 2):
- L’intervallo [-\frac{7}{2}, 5], che contiene tutti i termini della successione
- L’intervallo [-1, 2], che contiene tutti i termini della successione, tranne due
Utilizzando il linguaggio statistico, si direbbe che i termini a_4 ed a_7 sono degli outlier, ossia dei valori che chiaramente si discostano dall’andamento generale degli altri, e per questo trascurabili. Nella statistica descrittiva, due possibili analisi che si possono effettuare su un campione di dati sono proprio l’individuazione degli outlier e di alcuni intervalli che contengono la maggior parte dei dati, un po’ come abbiamo fatto finora con la nostra successione. Il paragone con la statistica però si ferma qui, perché c’è una grande differenza tra lo studio di un campione statistico e lo studio di una successione: la successione è una sequenza infinita di dati, mentre un campione statistico è finito. Questo cambia molte cose. Ad esempio potremmo chiederci:
- Se il valore 5 fosse ripetuto all’infinito, ma solo ogni 1000 termini della successione, sarebbe ancora trascurabile?
- Ha senso chiedersi quale sia un intervallo che contiene più del 99% dei termini della successione?
Le risposte ad entrambe le domande sono negative:
- Se il valore 5 fosse ripetuto ogni 1000 termini, sebbene possa intuitivamente considerarsi “raro”, sarebbe pur sempre ripetuto infinite volte! Una cosa è trascurare un solo valore anomalo, un’altra cosa è trascurarne infiniti.
- Il 99%, o qualunque percentuale fissata maggiore di 0, di una quantità infinita è sempre una quantità infinita. Non c’è una differenza numerica tra il 99%, il 50% o il 100% di infinito: sono tutti infiniti nella stessa misura.
Cerchiamo allora di capire cosa ha senso chiedersi quando si studia una successione, contenente infiniti termini. Un concetto importante su cui ci focalizzeremo nel seguito è la distinzione tra “tutto” e “quasi tutto”, che applicheremo ai termini della successione, ma che è definito più in generale su qualsiasi insieme di infiniti elementi. Vediamo di che si tratta:
- “Tutto” significa… proprio tutto l’insieme! Nessun elemento escluso.
- “Quasi tutto” significa tutto l’insieme, tranne una quantità finita di elementi.
Applicando questo concetto all’insieme dei termini di una successione, possiamo dire che ha senso chiedersi:
- Qual è un intervallo che contiene tutti i termini della successione
- Qual è un intervallo che contiene quasi tutti i termini della successione
Come abbiamo visto, nel caso della successione mostrata in Figura 1, un intervallo che ne contiene tutti i termini è [-\frac{7}{2}, 5], mentre uno che li contiene quasi tutti è [-1, 2]; infatti quest’ultimo intervallo contiene tutti i termini tranne due, che è una quantità finita. Questi intervalli sono particolari, perché sono anche i più piccoli possibili, ciascuno per la propria categoria di appartenenza. Infatti:
- Anche [-4, 6], [-5, 10], [-10, 10], … sono intervalli che contengono tutti i termini della successione, ma non sono i più piccoli con questa caratteristica. Il più piccolo è [-\frac{7}{2}, 5] perché, se lo restringessimo a destra, non includerebbe il termine a_4 = 5; se lo restringessimo a sinistra, non includerebbe il termine a_7 = -\frac{7}{2}.
- Anche [-2, 5], [4, 4] e [-3, 4] sono intervalli che contengono quasi tutti i termini della successione, ma non sono i più piccoli intervalli con questa caratteristica. Il più piccolo è [-1, 2] perché, se lo restringessimo a destra, non includerebbe tutti i termini della successione pari a 2, che sono infiniti; analogamente, se lo restringessimo a sinistra, non includerebbe tutti i termini pari a -1, che sono anch’essi infiniti.
Abbiamo già usato diverse volte la parola “infinito”, e continueremo ad usarla spesso in questo articolo. È bene precisare che ci stiamo sempre riferendo ad un infinito di tipo numerabile, ossia lo stesso tipo di infinito dell’insieme dei numeri naturali. Esistono altri tipi di infinito che sono detti non numerabili, ma non li consideriamo in questo articolo.
Estremo inferiore, estremo superiore, limite inferiore e limite superiore di una successione reale
A questo punto ci potremmo chiedere: esiste sempre, per qualsiasi successione, il più piccolo intervallo che ne contiene tutti i termini, o il più piccolo che ne contiene quasi tutti?
La risposta è tutt’altro che banale. Per il primo quesito è affermativa, considerando gli intervalli chiusi:
Esistenza del più piccolo intervallo chiuso che contiene tutti i termini di una successione
Per ogni successione reale (a_n), esiste uno e un solo intervallo chiuso che:
- Contiene tutti i termini della successione
- È il più piccolo intervallo chiuso con la precedente proprietà
Cosa si intende esattamente per “intervallo più piccolo”?
Quando in matematica si parla di un oggetto che è più piccolo, o più grande, di un altro, bisognerebbe sempre chiarire in che senso. Quando si parla di numeri interi o reali, la questione è abbastanza banale, ma se abbiamo due intervalli I e J, come facciamo a stabilire quale dei due è il più piccolo? Ci sono almeno due modi:
- L’intervallo più piccolo è quello che ha ampiezza minore (dove l’ampiezza è data dalla differenza tra i due estremi)
- L’intervallo più piccolo è quello che è contenuto nell’altro
Entrambi questi modi di intendere il concetto di intervallo più piccolo hanno i propri problemi:
- Se ci si basa sull’ampiezza, non si possono trattare adeguatamente gli intervalli illimitati. Ad esempio gli intervalli [-1, +\infty], [-\infty, 1000] e [-\infty, +\infty] hanno tutti la stessa ampiezza (infinita), ma sono molto diversi tra loro.
- Se ci si basa su quale intervallo contiene l’altro, si possono confrontare facilmente alcuni intervalli illimitati tra loro (per esempio [-1, +\infty] è più grande di [3, +\infty], perché lo contiene). D’altra parte, molte coppie di intervalli non sono confrontabili, nel senso che non si può stabilire qual è il più piccolo (ad esempio gli intervalli [0, 2] e [1, 3] non sono confrontabili, perché nessuno dei due contiene l’altro).
In questo articolo utilizzeremo la seconda definizione, quella basata sul contenimento. Questa definizione è anche la più generale, essendo applicabile ad insiemi qualsiasi, non solo ad intervalli. L’uso di una definizione piuttosto che di un’altra comunque ha un’importanza relativa in questo articolo, perché tutto quello che diremo, con piccole modifiche di forma, varrebbe anche se si confrontassero gli intervalli per ampiezza.
La seguente proprietà, di cui tralasciamo la dimostrazione, permette di definire l’estremo inferiore (\inf) e l’estremo superiore (\sup) di una successione reale, che sono semplicemente gli estremi dell’intervallo individuato dalla Proprietà A.1:
\inf e \sup di una successione reale
Data una successione reale (a_n), sia I = [i, s] il più piccolo intervallo chiuso che contiene tutti i termini della successione. Allora si definiscono:
Ad esempio, nel nostro caso:
Si può notare che nella Definizione A.5 non è specificato se l’\inf e il \sup sono due termini della successione. Nella successione a_n della Figura 2 è così, ma in generale l’\inf e il \sup potrebbero essere solamente dei valori limite che di fatto non corrispondono a nessun termine particolare. Ad esempio, l’\inf della successione 1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \ldots è 0, ma nessun termine della successione è uguale a zero.
Nel caso di successioni non limitate, l’\inf o il \sup possono essere infiniti. In questo caso l’intervallo I della Definizione A.5 può essere del tipo [-\infty, s], [i, +\infty] o [-\infty, +\infty]. Ad esempio, la successione di Fibonacci 1, 2, 3, 5, \ldots (in cui ogni termine è la somma dei due precedenti) ha come \inf 1 e come \sup +\infty. Si noti che gli intervalli del tipo [-\infty, s], [i, +\infty] o [-\infty, +\infty] sono comunque chiusi, come richiesto dalla Definizione A.5. Infatti +\infty e/o -\infty, a seconda dei casi, appartengono a tali intervalli, come se fossero dei numeri reali. Gli intervalli [-\infty, s], [i, +\infty] e [-\infty, +\infty] non sono quindi intervalli in \mathbb{R}, ma nell’insieme \mathbb{R} \cup \{-\infty, +\infty\}.
La Definizione A.5 definisce simultaneamente l’\inf e il \sup di una successione, ma c’è anche il modo di definirli in modo separato. Vediamo questa definizione alternativa, che è quella canonica:
\inf e \sup di una successione reale, definizione canonica
Data una successione reale (a_n), si definiscono:
Le due definizioni sono equivalenti, nel senso che, se si assume la Definizione A.5 come definizione di \inf e \sup, allora la Definizione A.6 si può dimostrare come proprietà; viceversa, se si parte dalla Definizione A.6 allora si può dimostrare la Definizione A.5 come proprietà. In questo articolo abbiamo scelto come definizione la A.5 perché la riteniamo più semplice ed intuitiva.
Sulla base dell’esempio precedente, si sarebbe tentati di dire che vale una proprietà analoga alla Proprietà A.1 per quanto riguarda gli intervalli che contengono quasi tutti i termini della successione, ossia che ne esiste sempre uno che è il più piccolo. Vedremo che invece questo non è vero, prendendo come esempio la successione mostrata in Figura 3.
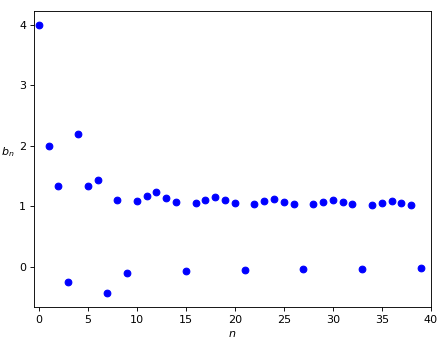
Questa successione, che chiameremo (b_n)_{n \geq 0}, è definita partendo da (a_n), come segue:
Come è evidente dal grafico, i termini positivi della successione tendono ad 1, mentre quelli negativi tendono a zero. La successione nel complesso non ha limite, ma è suddivisibile in due sottosuccessioni che hanno due limiti diversi. Ma non è questa la vera differenza rispetto alla precedente successione a_n, perché anche in a_n si possono trovare delle sottosuccessioni che hanno un limite: ad esempio i termini a_0, a_6, a_{12}, a_{18}, \ldots, a_{6k}, \ldots sono tutti uguali a 2, quindi a maggior ragione hanno come limite 2.
La differenza più importante tra le successioni (a_n) e (b_n) è che nella prima esiste il più piccolo intervallo che contiene quasi tutti i termini della successione, nella seconda no. Vediamo perché. Innanzitutto nella successione (b_n) nessun termine è uguale a 1 o a 0, anche se i termini positivi tendono a 1 e quelli negativi tendono a 0: ciò è evidente dal grafico.
Perché nessun termine della successione b_n è uguale a 1 o a 0?
Il motivo è molto semplice. Qualunque termine della successione b_n è dato dalla formula \frac{a_n + 1}{n + 1} + 1 o dalla formula \frac{a_n}{n}. Supponiamo che sia b_n = 0. Se b_n fosse ottenuto dalla formula \frac{a_n}{n} = 0, a_n dovrebbe essere 0, ma nessun termine della successione (a_n) è 0; se invece fosse ottenuto dalla formula \frac{a_n + 1}{n + 1} + 1 = 0, a_n dovrebbe essere -n - 2, ma non può essere perché, secondo la (1), la formula b_n = \frac{a_n + 1}{n + 1} + 1 = 0 vale solo quando a_n \gt 0. Si può ragionare allo stesso modo per dimostrare anche che nessun termine della successione è uguale a 1.
I valori 0 e 1 sono quindi dei limiti teorici che non vengono di mai fatto raggiunti: tutti i termini della successione sono o minori di 0, o maggiori di 1. Ne segue che l’intervallo [0, 1] non contiene nessun termine. Allora, se vogliamo trovare il più piccolo intervallo che contiene quasi tutti i termini della successione, dobbiamo estendere l’intervallo [0, 1] sia a destra che a sinistra, per includere sia i termini maggiori di 1 che quelli minori di 0 (entrambi infiniti).
In realtà, si può dimostrare che qualunque intervallo più grande di [0, 1] contiene quasi tutti i termini della successione, e che non ne esiste uno che è più piccolo di tutti gli altri.
Perché qualunque intervallo più grande di [0, 1] contiene quasi tutti i termini della successione, e non ne esiste uno che è più piccolo di tutti gli altri?
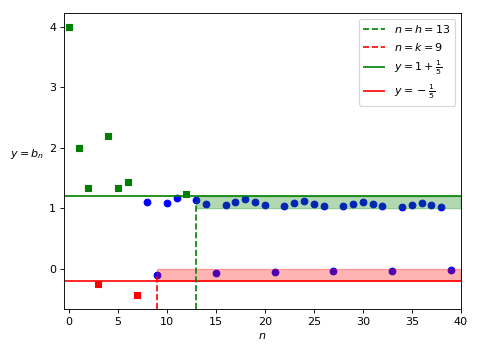
Supponiamo per semplicità di estendere l’ampiezza dell’intervallo della stessa quantità sia a destra che a sinistra; ad esempio, se come quantità scegliamo \frac{1}{5} otteniamo l’intervallo I := [0 -\frac{1}{5}, 1 + \frac{1}{5}] = [-\frac{1}{5}, \frac{6}{5}]. Quanti termini della successione contiene questo intervallo?
Cominciamo da quelli negativi. Dato che essi tendono a zero, diventando sempre più piccoli in valore assoluto, da un certo punto della successione in poi (cioè “definitivamente”, per usare la terminologia dell’analisi asintotica) essi saranno sempre maggiori o uguali di -\frac{1}{5}. Esiste cioè una certa costante k tale che, per ogni n \geq k, tutti i termini b_n negativi sono maggiori o uguali di -\frac{1}{5}. Quindi gli unici termini della successione che possono essere negativi e non rientrare nell’intervallo I sono b_0, b_1, b_2, \ldots, b_{k-1}: si tratta di al più k termini (in realtà sono meno di k, perché i termini elencati comprendono anche quelli positivi; ma nella peggiore delle ipotesi, cioè se non ci fosse nessun termine positivo, sarebbero k).
Per i termini positivi possiamo ragionare in maniera analoga. Dato che essi tendono ad 1, diventando sempre più piccoli, essi saranno definitivamente minori o uguali di \frac{6}{5}. Esiste cioè una certa costante h tale che, per ogni n \geq h, tutti i termini b_n positivi sono minori o uguali di \frac{6}{5}. Quindi gli unici termini della successione che possono essere positivi e non rientrare nell’intervallo I sono b_0, b_1, b_2, \ldots, b_{h-1}: si tratta di al più h termini.
Ricapitolando, al di fuori dell’intervallo I = [-\frac{1}{5}, \frac{6}{5}] possono esserci al più k + h termini della successione, cioè un numero finito. Quindi questo intervallo contiene quasi tutti i termini della successione (v. Figura 4).
Ma allora, se l’intervallo [0, 1] non contiene nessun termine b_n, e l’intervallo [-\frac{1}{5}, \frac{6}{5}] li contiene quasi tutti, certamente il più piccolo intervallo che contiene quasi tutti i termini deve essere intermedio tra i due. Tuttavia, per quanto possiamo sforzarci di cercare questo intervallo, non lo troveremmo mai… perché non esiste! Infatti, come per costruire l’intervallo I siamo partiti dall’intervallo [0, 1] allargandolo di \frac{1}{5} a destra e a sinistra, se al posto di \frac{1}{5} considerassimo un’altra costante positiva \epsilon, ottenendo l’intervallo I_{\epsilon} := [-\epsilon, 1 + \epsilon], non cambierebbe nulla, perché anche questo intervallo conterrebbe quasi tutti i termini, per qualsiasi \epsilon. Infatti, anche supponendo che la costante \epsilon sia molto piccola, esisteranno sempre degli indici k_{\epsilon} e h_{\epsilon} tali che tutti i termini negativi della successione di indice maggiore o uguale di k_{\epsilon} sono maggiori o uguali di -\epsilon, e tutti i termini positivi di indice maggiore o uguale di h_{\epsilon} sono minori o uguali di 1 + \epsilon. Più è piccolo \epsilon, più saranno grandi k_{\epsilon} e h_{\epsilon}, ma essi saranno pur sempre finiti. Quindi l’intervallo I_{\epsilon} esclude al più k_{\epsilon} + h_{\epsilon} termini della successione, ossia un numero finito, quindi li contiene quasi tutti.
Da ciò si può dedurre che non esiste un intervallo più piccolo che contiene quasi tutti i termini della successione. Ciò deriva dal fatto che non esiste un numero reale positivo che è più piccolo di tutti (a differenza dei numeri interi). Infatti, abbiamo visto che qualunque costante \epsilon \gt 0 determina un intervallo I_{\epsilon} = [-\epsilon, 1 + \epsilon] che contiene quasi tutti i termini della successione; diminuendo \epsilon questo intervallo si riduce sempre di più, ma non esiste un intervallo più piccolo di tutti, perché non esiste un \epsilon positivo più piccolo di tutti.
Ricapitolando, abbiamo visto che l’intervallo [0, 1], pur non contenendo nessun termine della successione (b_n), ha una proprietà particolare: qualunque intervallo che lo contiene propriamente, contiene quasi tutti i termini della successione. In altre parole, si passa da zero a quasi tutti i termini anche con un piccolissimo ampliamento dell’intervallo, senza vie di mezzo. Ma un’altra cosa interessante è che l’intervallo [0, 1] è il più piccolo intervallo con questa proprietà. Infatti, si può dimostrare che la proprietà vale anche per tutti gli intervalli più grandi di [0, 1], mentre non vale per tutti quelli più piccoli:
- Abbiamo detto che, se A è un intervallo più grande di [0, 1], contiene quasi tutti i termini della successione. Allora la proprietà vale per A in quanto, se già A stesso contiene quasi tutti i termini, a maggior ragione questo sarà vero anche per qualunque intervallo più grande di A.
- Se B è un intervallo più piccolo di [0, 1], la proprietà non vale per B, perché non è vero che tutti gli intervalli più grandi di B contengono quasi tutti i termini della successione; infatti [0, 1] è più grande di B ma non contiene nessun termine.
Quindi [0, 1] non è il più piccolo intervallo che contiene quasi tutti i termini della successione (che non esiste), ma il più piccolo intervallo tale che qualunque intervallo più grande contiene quasi tutti i termini della successione. Si può dimostrare (ma non lo facciamo) che un tale intervallo esiste per ogni successione reale:
Esistenza del più piccolo intervallo tale che qualunque intervallo più grande contiene quasi tutti i termini di una successione reale
Per ogni successione reale (a_n), esiste un intervallo tale che:
- Qualunque intervallo più grande contiene quasi tutti i termini della successione
- È il più piccolo intervallo con la precedente proprietà
Si può osservare che l’intervallo che soddisfa la Proprietà A.2 non contiene necessariamente esso stesso quasi tutti i termini della successione: sono gli intervalli più grandi che li contengono. Questo è proprio ciò che accade nel nostro esempio: l’intervallo [0, 1] non contiene quasi tutti i termini della successione, anzi non ne contiene proprio nessuno!
Proprio come la Proprietà A.1 ci ha consentito di definire l’\inf e il \sup di una successione, così la Proprietà A.2 ci consente di definire il \lim \inf e il \lim \sup, che sono gli estremi dell’intervallo che la soddisfa:
\lim \inf e \lim \sup di una successione reale
Data una successione reale (a_n), sia I = [i, s] l’intervallo che soddisfa la Proprietà A.2. Allora si definiscono:
Nel caso della successione b_n, come abbiamo visto:
Definizione alternativa di \lim \inf and \lim \sup
Come abbiamo puntualizzato prima a proposito dell’\inf e del \sup, analogamente la definizione canonica del \lim \inf e del \lim \sup di una successione non è la Definizione A.7, ma la seguente, che li definisce in modo separato:
\lim \inf e \lim \sup di una successione reale, definizione canonica
Sia (a_n) una successione reale.
Si definisce \lim \sup a_n il numero reale s tale che:
- Se (a_n) è limitata superiormente:
- Quasi tutti i termini della successione sono minori o uguali di s
- È il più piccolo numero con la precedente proprietà
- Altrimenti, s = +\infty
Si definisce \lim \inf a_n il numero reale i tale che:
- Se (a_n) è limitata inferiormente:
- Quasi tutti i termini della successione sono maggiori o uguali di i
- È il più grande numero con la precedente proprietà
- Altrimenti, i = -\infty
Come le Definizioni A.5 ed A.6, così anche le Definizioni A.7 ed A.8 sono equivalenti: scelta una delle due, l’altra si può dimostrare come proprietà.
Relazione tra limite superiore, limite inferiore e limite di una successione
Concludiamo enunciando due importanti proprietà che legano il \lim \inf ed il \lim \sup di una successione, da una parte, ed il limite della stessa, dall’altra parte.
Abbiamo visto che, nella successione (b_n) mostrata in Figura 3, il \lim \inf e il \lim \sup sono diversi, e la successione non ha limite, ma oscilla continuamente tra il \lim \inf (0) e il \lim \sup (1), avvicinandosi ora all’uno ora all’altro. Questa caratteristica non riguarda solo il nostro esempio, ma vale in generale. Infatti si può dimostrare la seguente Proposizione:
Ogni successione reale avente \lim \inf e \lim \sup diversi non ammette limite
Ogni successione reale (a_n) tale che \lim \inf a_n \neq \lim \sup a_n non ammette limite.
Vediamo invece cosa accade quando \lim \inf e \lim \sup sono uguali.
Consideriamo a tal proposito la successione (c_n) definita come segue:
Disegnando il grafico si vede chiaramente che questa successione tende a zero:
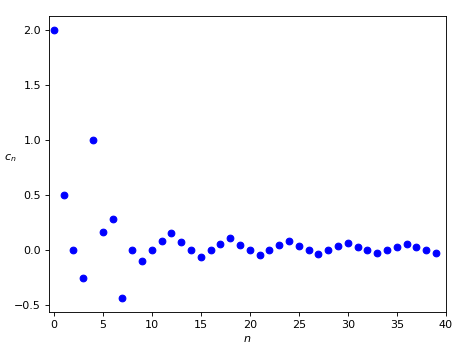
Chiediamoci ora: in base alla Definizione A.7, quali sono il \lim \inf e il \lim \sup di questa successione? Cominciamo, come prima, dall’analisi degli intervalli che contengono quasi tutti gli elementi della successione. Intuitivamente, dato che i termini della successione tendono a concentrarsi attorno allo zero, sia sopra che sotto, un intervallo che li contiene quasi tutti deve necessariamente contenere lo zero.
In realtà, analogamente a prima, si può dimostrare che qualunque intervallo che contiene al suo interno lo zero, contiene quasi tutti i termini della successione.
Possiamo considerare per semplicità un intervallo con la stessa ampiezza a destra e a sinistra dello zero, cioè del tipo [-\epsilon, \epsilon], per qualche costante \epsilon \gt 0. In effetti, si può dimostrare (utilizzando la definizione di limite) che un tale intervallo contiene, per qualunque \epsilon, quasi tutti i termini della successione, in particolare tutti i termini con indice maggiore o uguale di una certa costante k_{\epsilon} \gt 0 (v. Figura 6).
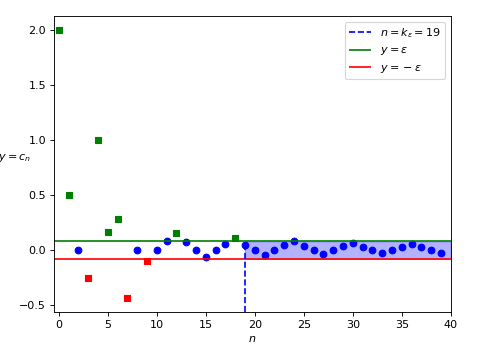
Torniamo allora allo stesso discorso di prima: diminuendo \epsilon possiamo trovare infiniti intervalli del tipo [-\epsilon, \epsilon], tutti i quali contengono quasi tutti i termini della successione.
Ma noi vogliamo trovare un intervallo chiuso che soddisfi la Definizione A.7. Questo intervallo deve essere quindi più piccolo di tutti gli intervalli che contengono 0 al loro interno… Allora c’è una sola possibilità, ed è un intervallo molto particolare: si tratta dell’intervallo [0, 0], avente 0 come entrambi gli estremi, quindi non come punto interno. È praticamente l’insieme ridotto al solo numero 0, ma è pur sempre un intervallo chiuso, ed inoltre soddisfa la Definizione A.7.
L’intervallo [0, 0] soddisfa la Definizione A.7 perché ne soddisfa entrambi i punti:
- Tutti gli intervalli del tipo [-\epsilon, \epsilon], che sono più grandi di [0,0], contengono quasi tutti i termini della successione (la stessa cosa vale per qualsiasi intervallo più grande, anche con estremi diversi in valore assoluto, ma per semplicità non consideriamo questo caso più generale).
- Quanto al fatto di essere il più piccolo intervallo con la precedente proprietà, il problema non si pone nemmeno, perché essendo esso già ridotto ad un solo punto, non esistono intervalli più piccoli (l’insieme vuoto non è un intervallo).
Quindi, in base alla Definizione A.7:
Si può notare una forte analogia tra questa successione e la precedente: ad esempio, come l’intervallo [0,1] non contiene nessun termine della successione (b_n), così anche l’intervallo [0,0] non contiene nessun termine di (c_n).
Tra le due successioni vi è però una differenza sostanziale: la successione (c_n) ammette limite, ed il suo \lim \inf coincide col suo \lim \sup, mentre la successione (b_n) ha \lim \inf e \lim \sup diversi e, per la Proposizione A.1, non ammette limite. Anche nel caso di (c_n), il legame che si osserva tra il limite inferiore, il limite superiore e il limite vale in generale per qualsiasi successione reale:
Ogni successione reale avente \lim \inf e \lim \sup uguali ammette limite
Ogni successione reale (a_n) tale che \lim \inf a_n = \lim \sup a_n ammette limite, e \lim a_n = \lim \inf a_n = \lim \sup a_n.
Unendo le Proposizioni A.1 e A.2, si ottiene immediatamente la seguente Proprietà:
Una successione reale ammette limite se e solo se il suo \lim \inf e il suo \lim \sup coincidono.
Una successione reale (a_n) ammette limite se e solo se \lim \inf a_n = \lim \sup a_n, ed in tal caso \lim a_n = \lim \inf a_n = \lim \sup a_n.
Teoricamente si potrebbe utilizzare la precedente Proprietà come definizione del limite di una successione: in questo modo il limite di una successione sarebbe definito non come entità a sé stante, ma sulla base del limite inferiore e superiore.
Nel prossimo articolo applicheremo questa Proprietà alla funzione \frac{\pi(x)}{x}.
Grazie per la spiegazione chiara ed intuitiva! Ci stavo sbattendo la testa da un pò..