Prerequisiti:
- Il postulato di Bertrand
- Il prodotto dei primi numeri primi: una maggiorazione
- Logaritmi e loro proprietà
- Massimo comun divisore e minimo comune multiplo
Sappiamo che un modo per calcolare il minimo comune multiplo tra due o più numeri è scomporli in fattori primi, e poi prendere ciascun fattore primo distinto con la massima potenza con cui compare in uno dei numeri considerati. Procedendo così, si otterrà la fattorizzazione del minimo comune multiplo. Ad esempio, volendo calcolare il minimo comune multiplo tra 4 = 2^2, 6 = 2 \cdot 3 e 45 = 3^2 \cdot 5, vediamo che i fattori primi distinti sono 2, 3 e 5; il 2 compare con esponente massimo 2 nel 4, il 3 compare con esponente massimo 2 nel 45, il 5 compare con esponente massimo 1 sempre nel 45; per cui il minimo comune multiplo cercato è 2^2 \cdot 3^2 \cdot 5 = 180.
Esiste un caso particolarmente interessante in cui si può calcolare il minimo comune multiplo attraverso un ragionamento, senza scomporre i numeri in fattori primi: è il calcolo del minimo comune multiplo dei numeri interi positivi fino ad un certo numero x, ossia \mathrm{MCM}(1, 2, \dots, x). Naturalmente questa espressione coincide con \mathrm{MCM}(2, \dots, x) per x \geq 2, dato che in questo caso il numero 1 non apporta alcun contributo nel calcolo. Questa quantità, in funzione di x, è così importante in teoria dei numeri che conviene indicarla con una notazione specifica:
Minimo comune multiplo degli interi positivi fino ad x
Si definisce la funzione
dove x > 0 è un intero.
Per arrivare a calcolare \psi^{\star}(x) senza una esplicita scomposizione in fattori primi, cominciamo a suddividere in due fasi il metodo di calcolo del minimo comune multiplo che già conosciamo:
- Individuazione dei numeri primi: scorriamo le fattorizzazioni dei numeri dati ed annotiamo quelli primi che troviamo, ignorando le ripetizioni;
- Ricerchiamo ciascun primo p, individuato nel passo precedente, nelle fattorizzazioni dei numeri dati ed annotiamo il massimo esponente con cui compare: quello sarà l’esponente di p nel risultato finale.
Nel caso dei numeri da 2 ad x, è immediato vedere che, scorrendo le loro fattorizzazioni, gli unici numeri primi che troveremo saranno quelli minori o uguali ad x: abbiamo quindi la risposta per il primo punto. Per quanto riguarda gli esponenti invece dobbiamo chiederci: dato un numero primo p \leq x, qual è il massimo esponente che esso può avere nelle fattorizzazioni dei numeri 2, \dots, x? Sembra una domanda complessa, ma basta osservare che questo esponente k non può superare \log_{p} x, dato che, per definizione di logaritmo, si scrive \log_{p} x = k per indicare che p^k = x; ma allora, dato che k è un numero intero, esso non può superare \left \lfloor \log_p x \right \rfloor. Ora consideriamo il numero intero p^{\left \lfloor \log_p x \right \rfloor}. Per costruzione è minore o uguale ad x, quindi abbiamo trovato un numero, tra quelli di cui calcolare il minimo comune multiplo, nella cui fattorizzazione p ha esponente \left \lfloor \log_p x \right \rfloor. Ma abbiamo detto che questo è l’esponente più grande possibile per p, dunque abbiamo trovato il massimo esponente richiesto nel secondo punto. Ricapitolando, possiamo enunciare la seguente Proposizione:
Calcolo di \psi^{\star}(x)
Per ogni intero x > 0:
Maggiorazioni e minorazioni
Possiamo fare un’importante osservazione guardando l’equazione (1). Nell’esponente di p, \left \lfloor \log_p x \right \rfloor, l’utilizzo della parte intera è stato necessario per il calcolo esatto di \psi^{\star}(x), ma se decidiamo di trascurarla abbiamo che
è un prodotto di termini tutti uguali ad x. Ma il numero di termini, dato dalla condizione p \leq x, è il numero di primi minori o uguali ad x:
La quantità all’esponente, che compare qui per la prima volta, è di centrale importanza in teoria dei numeri, pertanto ne forniamo una definizione:
Numero di primi minori o uguali ad x
Si definisce la funzione
dove x è un intero positivo.
Partendo dalle equazioni (2) e (3), utilizzando la Definizione N.6, otteniamo la seguente maggiorazione della funzione \psi^{\star}:
Maggiorazione di \psi^{\star}(x) mediante \pi(x)
Per ogni intero x > 0:
Possiamo ottenere anche una minorazione della funzione \psi^{\star}, partendo dal Lemma N.1 che abbiamo incontrato nel percorso verso il postulato di Bertrand. Questo Lemma è una proprietà della fattorizzazione di un particolare numero: il binomiale \binom{2n}{n}. Il Lemma asserisce che, nella fattorizzazione di questo numero, un numero primo p non può avere un esponente maggiore di \log_p 2n. Ma, essendo l’esponente di p un numero intero, ciò equivale a dire che esso non può superare \left \lfloor \log_p 2n \right \rfloor. Possiamo esprimere questo concetto con la seguente formula:
dove la produttoria è estesa a tutti i fattori primi del binomiale. Ma, come conseguenza della definizione del binomiale \binom{2n}{n}, come abbiamo osservato all’inizio dell’articolo sul postulato di Bertrand, i suoi fattori primi non possono essere maggiori di 2n, quindi possiamo estendere la produttoria considerando tutti i numeri primi minori o uguali a 2n, riallacciandoci così alla Proposizione N.2:
Questa disuguaglianza è una minorazione di \psi^{\star}(2n), cioè di \psi^{\star}(x) quando x è pari. Ora dobbiamo:
- Estenderla al caso di x dispari;
- Eliminando il binomiale per renderla facilmente trattabile mediante l’analisi asintotica.
Così facendo, si ottiene la seguente disuguaglianza:
Minorazione di \psi^{\star}(x)
Per ogni intero x > 0:
Essa ci permetterà, già nel prossimo articolo, di ottenere un teorema sorprendentemente simile al Teorema dei numeri primi.
Per quanto riguarda l’eliminazione del binomiale, in vista di adoperare gli strumenti dell’analisi asintotica, conviene partire già da ora con delle funzioni più semplici possibili. Perciò utilizziamo la Proprietà N.3, ottenendo che \sqrt{2^{2n}} \leq \binom{2n}{n}, dove il primo termine si semplifica in 2^n, per cui
Unendo la (4) e la (5) otteniamo quindi
Ora se x è pari possiamo porre 2n := x e sostituire nella (6), ottenendo:
Dalla Definizione N.5 possiamo notare che la funzione \psi^{\star} è strettamente crescente, ossia
dove la limitazione x \geq 2 è necessaria per fare in modo che l’argomento di \psi^{\star}(x - 1) sia almeno 1, come richiede la definizione. Se nella (8) supponiamo x dispari (ed in particolare x \geq 3, vista la limitazione), certamente x - 1 è pari, dunque possiamo utilizzare la (7) con x - 1 al posto di x ed estendere così la (8):
Questo vale per ogni x dispari maggiore o uguale a 3. Tra le possibili x dispari resta fuori solo il caso x = 1 che discuteremo a parte.
Riconciliando la (9), che vale per i numeri dispari maggiori o uguali a 3, con la (7), che vale per i pari, possiamo scrivere:
Infatti \left \lfloor \frac{x}{2} \right \rfloor è uguale a \frac{x}{2} se x è pari; \frac{x - 1}{2} se x è dispari.
La parte intera può dare fastidio nei calcoli, per cui è bene eliminarla, osservando ad esempio che \left \lfloor \frac{x}{2} \right \rfloor \geq \frac{x}{3} per ogni x \geq 2. Quindi il termine a sinistra può essere a sua volta minorato con 2^{\frac{x}{3}} = \sqrt[3]{2^x}:
Resta da esaminare il caso x = 1, per il quale la (10) continua a valere: infatti \sqrt[3]{2} \leq \psi^{\star}(1) = 1. Quindi la (10) vale in realtà per ogni possibile x, come asserito dalla Proposizione N.3.
Collegamento con la funzione \theta^{\star}(x)
Confrontiamo la (1) con la definizione della funzione \theta^{\star}(x):
Ciò che cambia sono gli esponenti dei primi p, che in \theta^{\star}(x) sono sempre 1, mentre in \psi^{\star}(x) dipendono da x. In effetti le due funzioni sono strettamente collegate tra loro, ed è importante stabilire esattamente come.
Per prima cosa, il prodotto (1) che definisce \psi^{\star}(x), con un po’ di fantasia può essere visto come il prodotto delle colonne di una opportuna tabella. Partendo poi da questa tabella, ma moltiplicandone le righe invece delle colonne, si ottiene lo stesso risultato (sempre \psi^{\star}(x)), ma in una forma diversa. Questo ragionamento, che vi invitiamo a leggere nel dettaglio, dà il nome al Lemma seguente:
Riformulazione di \psi^{\star}(x) (“calcolo per righe”)
Per ogni intero x > 0:
dove R := \left \lfloor \log_2 x \right \rfloor.
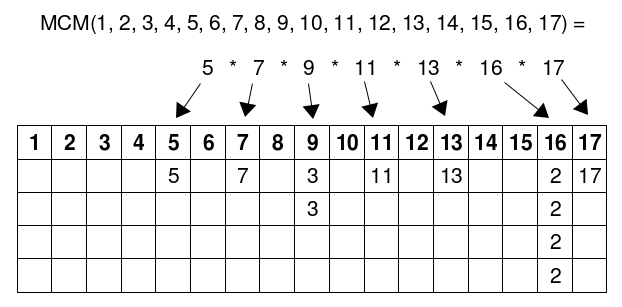
Nella (1), il primo p ha esponente \left \lfloor \log_p x \right \rfloor. Questo è, come abbiamo osservato all’inizio, l’esponente della più grande potenza intera di p minore o uguale ad x. Proviamo ad analizzare queste potenze, al variare di p, con l’ausilio di una tabella. Per ogni p consideriamo la colonna p^{\left \lfloor \log_p x \right \rfloor} e scriviamo p all’incrocio con la riga i = 1, 2, 3, \dots se e solo se i \leq \left \lfloor \log_p x \right \rfloor, cioè p^i \leq x. Ad esempio, per x = 17 abbiamo che:
- Per p = 2, la più grande potenza di p minore o uguale a 17 è 16 = 2^4, quindi scriviamo 2 all’incrocio tra la colonna 16 e le righe 1, 2, 3 e 4;
- Per p = 3, la più grande potenza di p minore o uguale a 17 è 9 = 3^2, quindi scriviamo 3 all’incrocio tra la colonna 9 e le righe 1 e 2;
- Per p = 5, la più grande potenza di p minore o uguale a 17 è 5 = 5^1, quindi scriviamo 5 all’incrocio tra la colonna 5 e la riga 1;
Procedendo in questo modo si ottiene la seguente tabella:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 5 | 0 | 7 | 0 | 3 | 0 | 11 | 0 | 13 | 0 | 0 | 2 | 17 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 |
Possiamo notare che la (1) è il prodotto dei numeri diversi da zero di questa tabella calcolato per colonne:
dove C_j è il prodotto dei numeri sulla colonna j. Alla fine abbiamo il prodotto dei numeri non nulli di tutte le colonne “piene”, cioè contenenti almeno un numero diverso da zero. Quindi possiamo dire che la Tabella 1 è solo un modo alternativo di scrivere il minimo comume multiplo degli interi positivi minori o uguali a 17, come si può vedere nell’immagine seguente:
Con l’ausilio della Tabella 1 possiamo calcolare lo stesso prodotto, ma procedendo per righe. Indicando con R_i il prodotto dei numeri diversi da zero della riga i, si ha:
Ma chi sono R_1, R_2, R_3, R_4? Abbiamo detto che un primo p compare nella riga i se e solo se p^i \leq x; inoltre se vi compare, per come abbiamo costruito la tabella, vi compare una volta sola. Quindi nella riga 1 compaiono tutti e soli i primi minori o uguali ad x, nella riga 2 compaiono tutti e soli i primi p tali che p^2 \leq x e così via. Quindi la (11) si può sviluppare in questo modo:
Il ragionamento portato avanti per x = 17 vale per qualsiasi x; resta solo da capire come calcolare il numero di righe della tabella in funzione di x. Per come abbiamo costruito la tabella, per ogni primo p scriviamo nelle righe 1, 2, \dots, \left \lfloor \log_p x \right \rfloor. Quindi l’ultima riga della tabella su cui scriviamo almeno una volta è il massimo valore possibile di \left \lfloor \log_p x \right \rfloor, al variare di p. Ma questa quantità cresce al decrescere di p, perciò il massimo che cerchiamo è in generale \left \lfloor \log_2 x \right \rfloor (per x = 17 abbiamo, come previsto, \left \lfloor \log_2 17 \right \rfloor = 4).
Ricapitolando, possiamo generalizzare la (12) enunciando il Lemma N.2.
Partendo dalla (13), è facile stabilire il collegamento tra le funzioni \psi^{\star} e \theta^{\star}. Innanzitutto il primo fattore del prodotto, \prod_{p \leq x} p, è proprio \theta^{\star}(x). Per quanto riguarda il secondo fattore, la condizione p^2 \leq x equivale a p \leq \sqrt{x}, per cui \prod_{p^2 \leq x} p = \prod_{p \leq \sqrt{x}} p = \theta^{\star}(\sqrt{x}). Si può ragionare analogamente per gli altri fattori, fino a \prod_{p^R \leq x} p = \prod_{p \leq \sqrt[R]{x}} p = \theta^{\star}(\sqrt[R]{x}). Possiamo quindi esprimere il collegamento tra le due funzioni con la seguente Proposizione:
Collegamento tra le funzioni \psi^{\star} e \theta^{\star}
Per ogni intero x > 0:
dove R := \left \lfloor \log_2 x \right \rfloor.