Prerequisiti:
Le proprietà dei divisori dei numeri naturali che abbiamo visto nell’articolo precedente ci permettono di definire una funzione molto importante in teoria dei numeri, la funzione di Möbius, indicata col simbolo \mu. Essa viene utilizzata spesso nelle sommatorie la cui variabile non varia tra un minimo e un massimo, ma assume come possibili valori tutti e soli i divisori positivi di un numero naturale.
Generalizzazione delle due proprietà dei divisori e definizione della funzione di Möbius
Riprendiamo la Proprietà N.9 (Una proprietà del prodotto dei divisori di un numero intero positivo avente almeno due fattori primi distinti), secondo la quale, se n è un numero intero positivo avente almeno due fattori primi distinti, presi i suoi divisori privi di quadrati, il prodotto di quelli che sono il prodotto di un numero pari di fattori primi è uguale al prodotto di quelli che sono il prodotto di un numero dispari di fattori primi. Ad esempio, se n = 60:
dove a destra compaiono i divisori di 60 privi di quadrati che sono prodotto di un numero dispari di fattori primi (ad esempio 30 = 2 \cdot 3 \cdot 5), e a sinistra compaiono i suoi divisori privi di quadrati che sono prodotto di un numero pari di fattori primi (tra cui 1, prodotto di zero fattori primi).
La (1) si può riscrivere come segue:
In questa formulazione è evidente che i divisori che sono il prodotto di un numero pari di fattori primi sono elevati all’esponente 1, mentre quelli che sono il prodotto di un numero dispari di fattori primi sono elevati a -1. Possiamo scrivere in modo compatto quest’uguaglianza introducendo una funzione che, dato un divisore d di 60 privo di quadrati, restituisce l’esponente appropriato. Chiameremo questa funzione \mu. Possiamo definirla utilizzando le notazioni P_n e D_n introdotte con la Proprietà N.8:
per ogni d \in \{\text{divisori di } 60 \text{ privi di quadrati}\}.
Utilizzando questa notazione, la (2) si può riscrivere come segue:
Questa formula può essere resa ancora più semplice considerando anche i divisori di 60 che non sono privi di quadrati. Possiamo includere questi divisori nella (2) elevandoli ad un esponente nullo, in modo che non modifichino il prodotto finale:
Ora ci è utile estendere la precedente definizione di \mu, includendo anche i divisori che non sono privi di quadrati. A tale scopo, introduciamo le seguenti notazioni, che riprendono ed estendono quelle della Proprietà N.8, e che ci consentiranno di alleggerire le prossime formule:
Insiemi di divisori di un numero intero positivo
Sia n \in \mathbb{N}^{\star}. Si definiscono i seguenti insiemi:
- P_n := \left\{ \text{divisori di $n$ privi di quadrati che sono prodotto di un numero pari di fattori primi} \right\}
- D_n := \left\{ \text{divisori di $n$ privi di quadrati che sono prodotto di un numero dispari di fattori primi} \right\}
- Q_n := \left\{ \text{divisori di $n$ non privi di quadrati} \right\}
Si può osservare che ogni divisore di n appartiene ad uno ed uno solo degli insiemi P_n, D_n e Q_n. In altri termini, l’insieme \{P_n, D_n, Q_n\} è una partizione dell’insieme dei divisori di n.
Utilizzando la Definizione N.17, la funzione \mu può essere definita in modo più generale come segue:
per ogni d \in \{\text{divisori di $60$}\}.
Il vantaggio di questa definizione è che, partendo dalla (2′), otteniamo una semplice produttoria estesa a tutti i divisori di 60:
Questo procedimento può essere generalizzato per qualsiasi intero positivo n che soddisfa la Proprietà N.9, ossia avente almeno due fattori primi distinti, come segue:
dove la funzione \mu è definita come nella (3′), sostituendo n al posto di 60; quindi
per ogni d \in \{\text{divisori di $n$}\}.
Come si semplifica la formula (5) se n è privo di quadrati?
Se n è privo di quadrati, anche tutti i suoi divisori sono privi di quadrati, per cui
e
mentre
per cui la (5) diventa:
Possiamo osservare che la definizione di \mu data dalla (3”) non dipende da n, ma solo da d. Infatti, il fatto che un divisore d sia privo di quadrati, ed il fatto che esso sia il prodotto di un numero pari o dispari di fattori primi, dipende solo da d stesso, non dal numero di cui è divisore. Possiamo quindi definire \mu per qualunque intero positivo, che comunque continueremo a chiamare d per ricordarci che di solito è un divisore di qualche altro numero fissato in precedenza, pur irrilevante ai fini della definizione:
Funzione di Möbius
Si definisce la funzione \mu: \mathbb{N}^{\star} \rightarrow \{-1, 1, 0\} tale che:
per ogni d \in \mathbb{N}^{\star}. La funzione \mu è chiamata funzione di Möbius.
La (5) può essere considerata una forma alternativa della Proprietà N.9:
Una proprietà del prodotto dei divisori di un numero intero positivo avente almeno due fattori primi distinti
Sia n un numero intero positivo avente almeno due fattori primi distinti. Allora:
La funzione di Möbius può essere utilizzata per scrivere in modo diverso anche la Proprietà N.8 (Una proprietà del conteggio dei divisori di un numero intero maggiore di 1). Questa Proprietà afferma che, per ogni intero n \gt 1:
Per calcolare la cardinalità di un insieme finito, basta associare il numero 1 a ciascun elemento dell’insieme, e sommare il tutto:
Da cui, per la (6):
In pratica, la Proprietà N.8 afferma che, se si calcola 1 per ogni elemento di P_n e -1 per ogni elemento di D_n, e si somma il tutto, il risultato finale è zero.
In questo calcolo potrebbero rientrare gli eventuali divisori di n che non sono privi di quadrati (che quindi non appartengono né a P_n né a D_n, ma appartengono a Q_n): l’importante è contarli come 0, in modo che non influiscano sulla somma:
È evidente ora che quest’equazione si può esprimere in forma compatta utilizzando la definizione di \mu(d), che vale 1 se d \in P_n, -1 se d \in D_n, e 0 se d \in Q_n:
Abbiamo così ottenuto la seguente forma alternativa della Proprietà N.8:
Una proprietà del conteggio dei divisori di un numero intero maggiore di 1
Sia n \gt 1 un numero intero. Allora:
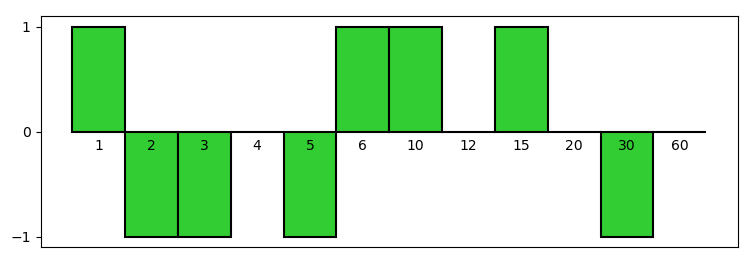
La Figura 1 visualizza questa Proprietà per n = 60. I valori della funzione di Möbius sono rappresentati come dei rettangoli, come nella Figura 1 dell’articolo Dai numeri interi ai numeri reali – seconda parte.
Connessione tra la funzione di Möbius e la funzione \Lambda
I vantaggi della funzione di Möbius non si limitano alla possibilità di scrivere in modo più conciso alcune formule. Il vantaggio principale è che essa si presta molto bene ad essere utilizzata in espressioni algebriche che coinvolgono sommatorie o produttorie estese a tutti i divisori di un certo numero naturale, come la (7). Come vedremo in seguito, in questo articolo e nei prossimi, le sommatorie di questo tipo sono molto comuni in teoria dei numeri. Prima di continuare, però, bisogna prima risolvere alcune piccole limitazioni delle Proprietà N.9 (seconda forma) e N.8 (seconda forma). La prima, infatti, vale solamente per i numeri interi positivi aventi almeno due fattori primi distinti, mentre la seconda vale solo per i numeri maggiori di 1. Per studiare adeguatamente le proprietà dei divisori dei numeri naturali, occorrono proprietà che siano valide per tutti i numeri interi positivi; possiamo trascurare solo lo 0, perché è l’unico numero naturale che, in base alla Definizione N.2 (Divisibilità) non ha divisori. Dunque, nella Proprietà N.9 (seconda forma) mancano i numeri interi positivi che hanno un solo fattore primo distinto (cioè le potenze con esponente positivo di un numero primo) ed il numero 1, che non ha fattori primi, mentre nella Proprietà N.8 (seconda forma) manca solo il numero 1. Cerchiamo ora di colmare queste mancanze.
Cominciamo dalla Proprietà N.9 (seconda forma). Innanzitutto, se n = 1, si ha:
dove abbiamo usato il fatto che \mu(1) = 1, perché 1 è privo di quadrati, non essendo divisibile per nessun quadrato maggiore di 1, ed è il prodotto di un numero pari (zero) di fattori primi.
Se invece n = p^a, con a \in \mathbb{N}^{\star}, bisogna osservare che i divisori di n sono 1, p, p^2, \ldots, p^a, e che tra questi solamente 1 e p sono privi di quadrati, ed essi sono rispettivamente il prodotto di un numero pari e di un numero dispari di fattori primi. Quindi:
Ricapitolando, possiamo dire che:
- se n è una potenza di un numero primo p con esponente positivo, allora \prod_{d \mid n} d^{\mu(d)} = \frac{1}{p};
- negli altri casi, ossia quando n = 1 oppure quando n è il prodotto di almeno due fattori primi distinti, \prod_{d \mid n} d^{\mu(d)} = 1.
Riconoscete qualcosa di familiare? Questa funzione è l’inverso della funzione \Lambda^{\star}, che abbiamo introdotto parlando del fattoriale; infatti \Lambda^{\star} vale p nel primo caso e 1 nel secondo. Possiamo allora generalizzare la Proprietà N.9 (seconda forma) come segue:
Una proprietà del prodotto dei divisori di un numero intero positivo
Sia n \in \mathbb{N}^{\star}. Allora:
Molte volte ci sarà utile anche la versione logaritmica di questa proprietà:
Una proprietà del prodotto dei divisori di un numero intero positivo
Sia n \in \mathbb{N}^{\star}. Allora:
Applicando il logaritmo ad ambo i membri della Proprietà N.10, ed utilizzando la definizione della funzione \Lambda, abbiamo:
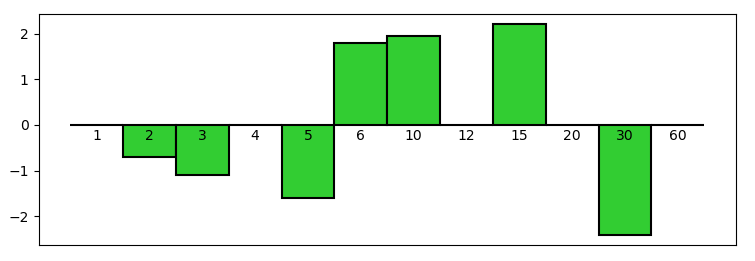
Quest’ultima Proprietà è visualizzata nella Figura 2, nel caso di n = 60.
Vediamo ora come possiamo estendere la Proprietà N.8 (seconda forma), considerando il numero 1. Se n = 1, si ha che:
Quindi possiamo dire che la funzione \sum_{d \mid n} \mu(d) è 1 se n = 1 e 0 altrimenti:
Una proprietà del conteggio dei divisori di un numero intero positivo
Sia n \in \mathbb{N}^{\star}. Allora:
Possiamo avere una prima idea di quanto la funzione di Möbius sia versatile nelle espressioni algebriche, sostituendo semplicemente \frac{n}{d} al posto di una d nella Proprietà N.10, come segue:
Il risultato è abbastanza sorprendente. Se per la Proprietà N.10 la produttoria \prod_{d \mid n} d^{\mu(d)} è pari a \frac{1}{\Lambda^{\star}(n)}, effettuando la sostituzione di cui sopra si ottiene esattamente l’inverso, ossia \Lambda^{\star}(n):
Espressione di \Lambda^{\star} mediante \mu
Sia n \in \mathbb{N}^{\star}. Allora:
Per dimostrare questa Proprietà, distinguiamo gli stessi casi che ci hanno portato alla dimostrazione della Proprietà N.10:
- n ha almeno due fattori primi distinti
- n è la potenza di un numero primo con esponente positivo
- n = 1
Innanzitutto possiamo riscrivere il prodotto \prod_{d \mid n} \left( \frac{n}{d} \right)^{\mu(d)} come segue:
Ritroviamo così, al denominatore, un prodotto che conosciamo, per la Proprietà N.10. Vediamo allora a cosa è uguale il numeratore. Si tratta di un altro prodotto, che possiamo spezzare distinguendo i tre tipi di divisori di n: quelli che appartengono a P_n, quelli che appartengono a D_n, e quelli che appartengono a Q_n. Ricordando che in questi tre casi il valore di \mu(d) è rispettivamente 1, -1 e 0, e ricordando che |P_n| = |D_n| per la Proprietà N.8, abbiamo che:
Allora, sostituendo nella (a) ed applicando la Proprietà N.10, otteniamo:
e questo completa la dimostrazione.
Come abbiamo fatto in precedenza per la Proprietà N.10, anche per la Proprietà N.12 possiamo enunciare la forma logaritmica:
Espressione di \Lambda mediante \mu
Sia n \in \mathbb{N}^{\star}. Allora: