Prerequisito:
Abbiamo notato che le funzioni \theta^{\star}(x) e \psi^{\star}(x) si comportano, in un certo senso, in maniera opposta. Infatti, confrontando la Proposizione N.3 (Minorazione di \psi^{\star}(x)) con la Proposizione N.1 (Maggiorazione del prodotto dei numeri primi fino ad x) si vede che, mentre \psi^{\star}(x) si presta ad essere minorata, \theta^{\star}(x) si presta ad essere maggiorata. La stessa cosa accade quando si introduce la funzione \pi(x): abbiamo visto nel Corollario della Proposizione N.2 che \psi^{\star}(x) può essere maggiorata da un’espressione contenente \pi(x); allo stesso modo, ora vedremo come \theta^{\star}(x) può essere minorata da un’espressione analoga.
Fissiamo un numero intero x e supponiamo che x \gt 1, in modo che vi sia almeno un primo fino a x. Un modo ovvio per minorare la funzione \theta^{\star} consiste nell’escludere alcuni dei primi coinvolti nel suo calcolo, cioè considerare il prodotto di un sottoinsieme di essi. Ma quali escludere? Dato che si tratta di effettuare una minorazione, essa è tanto migliore quanto più il numero ottenuto è grande, cioè vicino a \theta^{\star}(x). Allora la migliore minorazione possibile si ha escludendo i numeri primi più piccoli: potete capirlo facilmente con un esempio, come \theta^{\star}(7) = 2 \cdot 3 \cdot 5 \cdot 7: volendo escludere dal prodotto un numero primo, tra i quattro prodotti possibili (3 \cdot 5 \cdot 7, 2 \cdot 5 \cdot 7, 2 \cdot 3 \cdot 7 e 2 \cdot 3 \cdot 5), il più grande è proprio quello ottenuto escludendo il numero primo più piccolo, cioè 3 \cdot 5 \cdot 7.
È questo il principio alla base della minorazione di \theta^{\star}: dal prodotto completo si escludono i fattori primi più piccoli, e poi si cerca una stima per difetto del prodotto di quelli rimasti. In questo modo si ottiene il Lemma N.3.
Minorazione di \theta^{\star}(x) mediante \pi(x)
Per ogni numero reale \delta \geq 0 e per ogni x \gt 1:
Volendo possiamo includere anche il caso x = 1 mettendo \geq al posto di \gt. Questo comunque ha poca importanza, perché ci interessano i valori grandi di x.
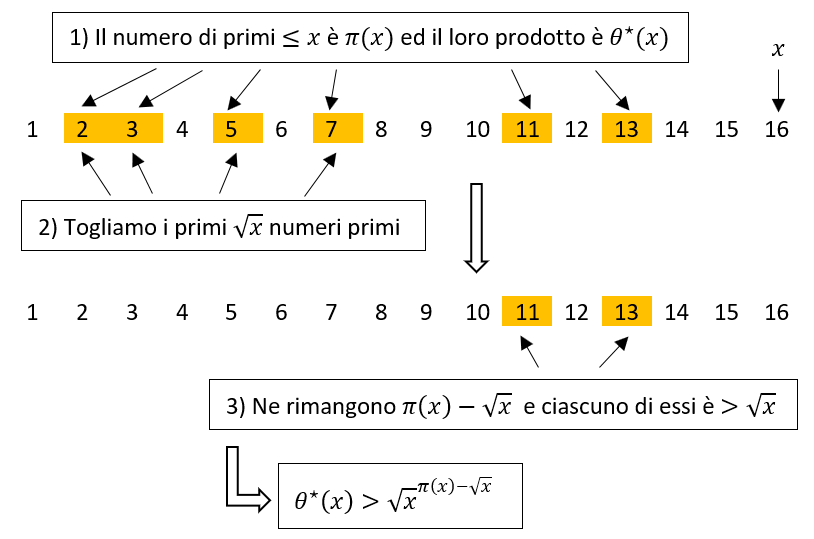
Abbiamo visto che, per ottenere una buona stima per difetto, conviene escludere, dal prodotto dei numeri primi fino a x, quelli più piccoli, partendo da 2 fino ad un certo p_i. Ma qual è questo p_i? Dove dobbiamo fermarci nel togliere i primi? È naturale che questo numero dipenda da x, come il numero totale di fattori primi, che è \pi(x). Le scelte più ovvie in questo caso sono \delta x o x^\delta, per qualche costante \delta. Ad esempio, per \delta = \frac{1}{2}, possiamo scegliere di escludere i primi \frac{x}{2} o i primi x^{\frac{1}{2}} = \sqrt{x} numeri primi (supponendo per il momento, per semplicità, che questi siano numeri interi). L’esperienza insegna che è più conveniente la seconda scelta. Il motivo è abbastanza sottile e lo vedremo nel prossimo articolo. Per il momento stabiliamo di escludere, dal prodotto \theta^{\star}(x), i primi \sqrt{x} numeri primi. Così facendo, il numero di primi considerati scende da \pi(x) a \pi(x) - \sqrt{x}. Tutto ciò naturalmente ha senso solo se \sqrt{x} \leq \pi(x), caso limite in cui elimineremmo tutti i fattori, ottenendo un prodotto di zero fattori che, come abbiamo convenuto, vale 1. Di certo non può essere \sqrt{x} \gt \pi(x): non possiamo eliminare più fattori di quanti ne abbiamo. Non conviene però perdersi in questi dettagli: andiamo avanti supponendo che \sqrt{x} \leq \pi(x) e alla fine vedremo se la conclusione a cui giungeremo è valida anche se questa supposizione fosse falsa.
Ora, osservando i \pi(x) - \sqrt{x} fattori rimanenti, notiamo che ciascuno di essi è maggiore di \sqrt{x}. Questo deriva da un principio generale. In una successione finita strettamente crescente di interi positivi 0 \lt a_1 \lt a_2 \lt \ldots \lt a_{n-1} \lt a_n, l’i-esimo elemento a_i è maggiore o uguale ad i (infatti a_1 \gt 0 \implies a_1 \geq 1, a_2 \gt a_1 \geq 1 \implies a_2 \geq 2, eccetera). Allora se togliamo i primi k elementi, cioè a_1, a_2, \ldots, a_{k}, gli elementi rimasti a_{k+1}, \ldots, a_{n-1}, a_{n} saranno tutti maggiori di k. Infatti, per l’osservazione precedente, a_{k+1} \geq k+1 \gt k ed i successivi elementi saranno anch’essi maggiori di k perché la succeessione è crescente. Nel nostro caso la successione strettamente crescente è quella dei numeri primi minori o uguali ad x: 2, 3, \ldots, p_{\pi(x) - 1}, p_{\pi(x)}, ed il numero k è \sqrt{x}. Dopo la rimozione, il più piccolo numero primo rimasto sarà p_{\sqrt{x} + 1} e, per questo semplice principio, possiamo essere certi che esso sarà maggiore di \sqrt{x}, come anche tutti gli altri primi rimasti, che saranno ancora più grandi.
Ricapitolando, dopo la rimozione restano \pi(x) - \sqrt{x} fattori primi, ciascuno dei quali maggiore di \sqrt{x}. Allora il loro prodotto è maggiore di
Essendo inoltre il prodotto dei fattori rimasti minore del prodotto completo, che è \theta^{\star}(x), abbiamo che
Tutto il ragionamento che ha portato alla formula (1) è riassunto nella seguente figura.
Se ora riconsideriamo l’ipotesi che \sqrt{x} \leq \pi(x), vediamo che non è poi così importante, perché la formula (1) vale in ogni caso: se \sqrt{x} \gt \pi(x), l’esponente è negativo ed il numero \sqrt{x}^{\pi(x) - \sqrt{x}} è minore di 1, e quindi anche di \theta^{\star}(x), che è almeno 1 (ricordiamo infatti che \theta^{\star}(1) = 1). Anche l’ipotesi che \sqrt{x} sia un numero intero non è fondamentale: in caso contrario il numero di fattori primi da togliere sarebbe \left \lfloor \sqrt{x} \right \rfloor, quelli rimasti sarebbero maggiori di \left \lfloor \sqrt{x} \right \rfloor, quindi almeno \left \lfloor \sqrt{x} \right \rfloor + 1 e perciò maggiori di \sqrt{x}, e la formula (1) diventerebbe
da cui si ottiene di nuovo la (1).
Questa approssimazione può sembrare grossolana per come è stata ottenuta, ma nasconde un grande potenziale. Infatti il ragionamento che abbiamo portato avanti con la radice quadrata di x, cioè x^{\frac{1}{2}}, può essere ripetuto analogamente con qualsiasi altra potenza di x con esponente reale \delta \geq 0 (non consideriamo le potenze negative perché in tal caso x^{\delta} sarebbe minore di 1, quindi non toglieremmo nessun numero primo e non varrebbe più il ragionamento svolto finora). Grazie a quest’ultima osservazione si ottiene appunto il Lemma N.3.
A titolo di esempio, applichiamo il Lemma per x = 64 e per due valori di \delta, \delta = \frac{1}{3} e \delta = \frac{1}{2}:
Entrambe, per il Lemma N.3, sono delle approssimazioni per difetto di \theta^{\star}(64) = 117.288.381.359.406.970.983.270. La seconda è un po’ più vicina al valore reale, ma sono entrambe molto lontane. Eppure, come vedremo nei prossimi articoli, questo tipo di approssimazione è sufficiente per dire qualcosa di interessante sui numeri primi.