Prerequisiti:
Se ci si sofferma a sufficienza ad osservare la successione dei numeri primi fino ad un certo numero x (per esempio https://primes.utm.edu/lists/small/1000.txt, si nota che è difficile trovare delle regolarità. Tuttavia questa successione gode di molte proprietà interessanti, alcune delle quali anche evidenti da un’analisi prettamente empirica, ma dalla difficile dimostrazione. Ciò che faremo da ora in avanti sarà esaminare sempre più a fondo la successione ricostruendo la catena di ragionamenti che porta fino al famoso Teorema dei numeri primi, evitando il più possibile di perdere il contatto coi numeri, sebbene lungo la strada introdurremo vari concetti “superiori”.
Un modo per cominciare ad indagare sulla successione dei numeri primi è considerarne, partendo dall’inizio, porzioni sempre più grandi. Ad esempio, si può partire con lo studio dei numeri primi fino a 10 (2, 3, 5, 7), poi fino a 20, fino a 30, eccetera, incrementando ogni volta di una quantità fissa la grandezza della porzione considerata. Oppure si può partire con lo studio dei numeri primi fino a 10, poi fino a 20, poi fino a 40, eccetera, raddoppiando di volta in volta la grandezza della porzione considerata. Quest’ultimo approccio si rivelerà efficace, in quanto basato sul prodotto. Infatti, essendo i numeri primi definiti partendo dai concetti di divisibilità (Definizione N.1) e di prodotto (Definizione N.2), è abbastanza naturale aspettarsi che, nello studio dei questi numeri, l’operazione principalmente utilizzata sia proprio il prodotto. In particolare, possiamo fissare un numero x e considerare il prodotto di tutti i numeri primi fino ad x. Chiameremo questa quantità, funzione di x, \theta^{\star}(x):
Prodotto dei primi fino ad x
Si definisce la funzione
Dove x è un intero positivo.
Si intende, d’ora in avanti, che la variabile p indica un numero primo. I casi banali sono:
- \theta^{\star}(1) = 1, perché non ci sono numeri primi fino a 1 e si assume che il prodotto di un insieme vuoto di termini sia 1 (nella pagina Definizione di un numero primo abbiamo già convenuto che il prodotto di un solo numero è il numero stesso);
- \theta^{\star}(2) = 2, perché 2 è l’unico numero primo fino a 2.
Un caso non banale si ha ad esempio per x = 20:
È un numero grande per il calcolo manuale, ma non ci interessa scriverlo esplicitamente.
Possiamo notare che \theta^{\star}(19) = \theta^{\star}(20), perché 20 non è primo. Ci fa comodo però partire da 20 che è un numero pari, perché in questo modo possiamo dividere l’insieme \{1, \dots, 20\} esattamente a metà, confrontando il prodotto dei numeri primi fino a 20 con quello dei numeri primi fino a 10:
Abbiamo 4 primi tra 1 e 10 ed altrettanti tra 10 e 20: si tratta di una coincidenza, infatti non è quasi mai verificato che tra un generico intero y e 2y vi sia lo stesso numero di numeri primi che vi sono tra 1 ed y, soprattutto al crescere di y.
Se moltiplichiamo \theta^{\star}(20) per i numeri non primi fino a 20, otteniamo il prodotto di tutti i numeri fino a 20, ossia 20! (il cosiddetto “fattoriale” di 20). Scriviamo questo prodotto evidenziando i numeri primi:
Possiamo fare la stessa cosa con x = 10:
Naturalmente il prodotto dei primi 10 numeri, che abbiamo nella (2), lo ritroviamo anche nella (1), per cui possiamo dividere membro a membro ed ottenere:
Ora abbiamo il prodotto dei numeri compresi tra 11 e 20, primi e non: sarebbe un’ottima cosa isolare tra questi i numeri primi, sopra evidenziati. Svolgere matematicamente questa operazione richiederebbe una conoscenza della successione dei primi che non abbiamo, tuttavia con un piccolo trucco è possibile fare qualcosa del genere.
Notiamo che l’espressione \frac{20!}{10!} ricorda molto il coefficiente binomiale
Di fatto per ottenere il coefficiente binomiale \binom{20}{10} partendo da \frac{20!}{10!} basta dividere ancora per 10!, per cui partendo dalla (3) si ottiene:
Ora torniamo ai numeri primi: volevamo separare il più possibile i numeri primi da quelli non primi, nella (3). Ebbene, dividendo per 10! abbiamo fatto proprio questo: infatti nessuno dei numeri primi evidenziati al numeratore della (4) divide 10!, perché sono tutti maggiori di 10, quindi nella divisione per 10! non possono essere eliminati. In pratica abbiamo trovato un divisore del prodotto (3) che contiene tutti i primi compresi tra 11 e 20. Facciamo esplicitamente la divisione per verificare che, in effetti, stiamo eliminando solo fattori non primi:
Abbiamo ottenuto il prodotto dei primi che cercavamo a meno di un fattore 4: non male per una tecnica così semplice.
Sostituendo nella (4) abbiamo:
In particolare, si ha sicuramente che:
In questa relazione c’è l’essenza di ciò che cerchiamo: una stima (in questo caso per eccesso) di un prodotto di numeri primi consecutivi, contenuti in un intervallo di numeri interi. Tuttavia, il ragionamento va ancora raffinato in quanto:
- Finora abbiamo tacitamente assunto che x sia pari: infatti, partendo da x = 20 abbiamo suddiviso l’insieme \{1, \dots, x\} in due parti esattamente equipotenti (cioè con lo stesso numero di elementi), ma ciò è possibile solo se x è pari. Bisogna vedere cosa succede se x è dispari.
- Ci serve una stima del prodotto di tutti i numeri primi fino a x, non solo quelli da un certo punto in poi. Bisogna iterare il procedimento per ottenere una stima che include anche i numeri primi mancanti.
- Il coefficiente binomiale non è un oggetto facilmente gestibile nei calcoli: possiamo maggiorare anche questo, sostituendolo con un’espressione più semplice. A questo proposito si possono utilizzare le stime che abbiamo visto nell’articolo Stime dei binomiali.
Per quanto riguarda il caso di x dispari, è sufficiente vedere cosa cambia tra lo sviluppo precedente, con x = 20, e lo sviluppo che si avrebbe con x = 21. In questo caso non possiamo partizionare l’insieme \{1, \dots, 21\} in due sottoinsiemi equipotenti, ma dobbiamo scegliere tra le partizioni \{\{1, \dots, 10\}, \{11, \dots, 21\}\} ed \{\{1, \dots, 11\}, \{12, \dots, 21\}\}.
Nel primo caso, il passaggio (3) diventerebbe:
Ora per ottenere un binomiale, come nel passaggio (4), dobbiamo procedere come segue:
Questo passaggio però non è nella logica di quanto svolto in precedenza, perché i numeri primi al numeratore non vengono tutti conservati, ma l’11 si semplifica.
Vediamo allora se le cose vanno diversamente nel secondo caso. Il passaggio (3) sarebbe:
Da cui, passando al binomiale più simile alla parte sinistra, abbiamo ancora \binom{21}{11}:
Ora non si semplifica nessun numero primo tra numeratore e denominatore, ma comunque abbiamo perso l’11. Quindi possiamo dire che in entrambi i casi stiamo parlando del prodotto dei numeri primi compresi tra 12 e 21, dove 12 è la metà di 21 approssimata per eccesso, ossia \left \lceil\frac{21}{2}\right \rceil. Questa volta semplificando abbiamo:
Da cui, sostituendo nella (6):
Quindi otteniamo l’analoga della (5):
Generalizzando questo procedimento, in modo tale che valga sia per i numeri pari che per quelli dispari, si ottiene, partendo da un intero x (rispettivamente 20 e 21 nella (5) e nella (5′)), la seguente stima per eccesso del prodotto dei numeri primi compresi tra \left \lceil\frac{x}{2}\right \rceil + 1 ed x:
Ricordiamo che \left \lceil\frac{x}{2}\right \rceil è la metà di x approssimata per eccesso, che però è semplicemente la metà di x se x è pari.
Passiamo ora al secondo punto. Partendo dalla (7), bisogna ottenere una stima per eccesso del prodotto completo dei numeri primi fino ad x:
Questo prodotto si può scrivere come il prodotto dei numeri primi compresi tra \left \lceil\frac{x}{2}\right \rceil + 1 ed x, per il prodotto dei numeri primi compresi tra 1 e \left \lceil\frac{x}{2}\right \rceil:
Il prodotto subito dopo l’uguale è dato dalla (7), per cui:
A questo punto, per l’ultimo prodotto si può applicare nuovamente la (7) con \left \lceil\frac{x}{2}\right \rceil al posto di x, ottenendo una maggiorazione del prodotto dei numeri primi compresi tra \left \lceil\frac{\left \lceil\frac{x}{2}\right \rceil}{2}\right \rceil + 1 e \left \lceil\frac{x}{2}\right \rceil. Iterando questo procedimento si ottiene:
Questo processo deve aver termine perché, continuando a dividere per due, a un certo punto si arriverà a 1 o a 2, e a quel punto non ha senso continuare a dividere, perché è noto il prodotto dei numeri primi fino a 2 (cioè 2 stesso) o fino a 1 (cioè 1): sono i casi banali della funzione \theta^{\star}, che abbiamo discusso inizialmente.
Ad esempio, per x = 21 si ha:
dove \binom{2}{1} = 2: a questo punto non ha senso continuare; anche se lo facessimo, otterremo un prodotto di infiniti 1 che non modifica in nessun modo la stima (9).
Resta ora il terzo punto: semplificare la (8) e la (9) sostituendo il binomiale con un’espressione più semplice da utilizzare nei calcoli. In particolare, utilizzeremo la Proprietà N.1, per la quale
I dettagli di come si arriva a questa formula si trovano nella pagina Stime dei binomiali. Qui però non interessa come si arriva alla formula, ma ci basta sostituirla nella (8) e nella (9) per ottenere delle stime più semplici per \theta^{\star}(x). Per semplicità proseguiamo con l’esempio numerico di x = 21:
Si può notare che, per passare da un esponente al successivo, bisogna dividere per due ed approssimare per difetto: 10 = \left \lfloor \frac{20}{2} \right \rfloor, 5 = \left \lfloor \frac{10}{2} \right \rfloor, 2 = \left \lfloor \frac{5}{2} \right \rfloor ed infine 1 = \left \lfloor \frac{2}{2} \right \rfloor. In particolare, nessun esponente può superare la metà del precedente: 10 \leq \frac{20}{2}, 5 \leq \frac{10}{2}, 2 \leq \frac{5}{2} ed infine 1 \leq \frac{2}{2}. Ciò è conseguenza del tipo di binomiali che stiamo utilizzando, dato dalla (8). Ad esempio, il primo binomiale è \binom{21}{11} = \binom{x}{\left\lceil\frac{x}{2}\right\rceil}, dal quale provengono i primi due esponenti 20 = 21 - 1 = x - 1 e 10 = 11 - 1 = \left\lceil\frac{x}{2}\right\rceil - 1. Il secondo esponente \left\lceil\frac{x}{2}\right\rceil - 1 non può superare \left(\frac{x}{2} + \frac{1}{2}\right) - 1, perché x è un intero e quindi, approssimando per eccesso \frac{x}{2}, possiamo aggiungere al massimo \frac{1}{2}. Ma \left(\frac{x}{2} + \frac{1}{2}\right) - 1 = \frac{x}{2} - \frac{1}{2} = \frac{x-1}{2}, che è proprio la metà del primo esponente. Questo dimostra che il secondo esponente non può superare la metà del primo, e questo meccanismo resta valido per tutti gli esponenti: allo stesso modo si dimostra che il terzo esponente non può superare la metà del secondo, cioè un quarto del primo, e così via:
Possiamo allora estendere la (10) con un’ulteriore disuguaglianza:
Questo discorso si generalizza facilmente ad un x generico:
Dove la somma 1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\dots+\frac{1}{2^k} si ferma al denominatore 2^k che è la più grande potenza di due minore o uguale ad x-1. Ma, per quanti termini di questa serie possiamo considerare, la loro somma sarà sempre al di sotto di un valore limite, che si indica con \sum_{n=1}^{\infty} \frac{1}{2^n} e che sappiamo essere 2:
Il fatto che questa somma limite esista e sia 2, è una facile applicazione della teoria delle serie numeriche. D’altra parte però, è facile comprendere come la somma a partire dal secondo termine, \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\dots+\frac{1}{2^k}, non possa superare 1 (da cui si ottiene che l’intera somma non può superare 2): basta immaginare un segmento di lunghezza unitaria del quale si taglia la metà (cioè \frac{1}{2}), poi la metà della rimanente metà (cioè \frac{1}{4}), ancora la metà, e così via: per quanto possiamo tagliare, la somma dei frammenti non potrà mai superare la lunghezza del segmento iniziale, cioè 1.
Sostituendo la (12) nella (11) si ottiene:
Alla fine otteniamo la seguente stima, per eccesso, del prodotto dei numeri primi fino ad x:
Maggiorazione del prodotto dei numeri primi fino ad x
Per ogni x > 0:
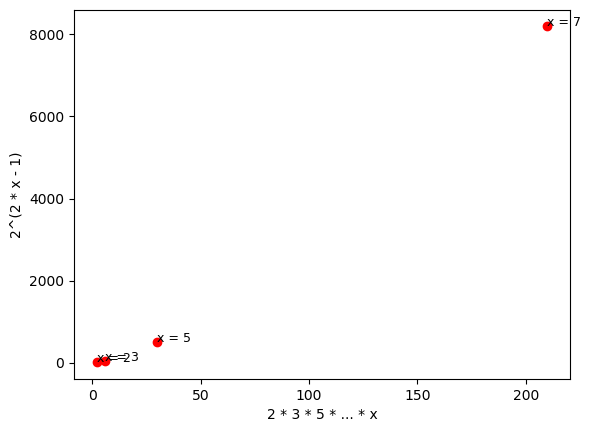
È interessante notare che la stima data dalla Proposizione N.1 non si può considerare buona, ai fini pratici: come si vede dai due grafici sottostanti, uno coi due assi nella stessa scala e l’altro con scale diverse, l’espressione 2^{2(x-1)} assume valori molto più alti del prodotto dei primi fino ad x, già per valori di x molto piccoli.