Prerequisiti:
- Elementi di analisi asintotica
- Il limite inferiore e il limite superiore di una successione
- Proprietà degli ordini asintotici
- Le funzioni W e V
- La media integrale e la funzione di errore assoluto R
- Una conseguenza del Teorema di Selberg, in forma integrale
Con questo articolo concluderemo la parte principale della dimostrazione del Teorema dei numeri primi, che si gioca tutta sulla relazione che intercorre tra le costanti \alpha e \beta che sono state introdotte nell’articolo La media integrale e la funzione di errore assoluto R, pari rispettivamente al limite superiore del valore assoluto della funzione V e al limite superiore della media integrale dello stesso valore assoluto. Per il Lemma N.7, per dimostrare il Teorema dei numeri primi è sufficiente dimostrare che \alpha = 0: in questo articolo ci avvicineremo a questo risultato.
Le due parti della dimostrazione del Teorema dei numeri primi
Per prima cosa ricordiamo le definizioni delle costanti \alpha e \beta (Definizione N.14):
dove x, come sempre sottinteso nei nostri articoli, è una variabile che assume solo valori interi (in questo caso solo valori interi positivi).
Come spesso accade in teoria dei numeri, le tecniche che utilizzeremo richiedono il passaggio dai numeri interi ai numeri reali. Definiremo perciò due nuove costanti, che chiameremo \alpha^{\prime} e \beta^{\prime}, che sono i corrispettivi di \alpha e \beta, dove la variabile rispetto a cui si calcola il limite superiore assume valori in un intervallo reale:
Costanti \alpha^{\prime} e \beta^{\prime}
Data la variabile \xi che può assumere valori nell’intervallo reale [1, +\infty), si definiscono le seguenti costanti:
dove per la variabile reale abbiamo utilizzato il simbolo \xi, la “x” greca, per ricordare che è il corrispettivo della variabile intera x della definizione di \alpha e \beta.
Quindi, rispetto ad \alpha, per calcolare \alpha^{\prime} si considerano tutti i valori della funzione f(\xi) := |V(\log \xi)| per \xi \in [1, +\infty), non solo per i valori interi di \xi (che sarebbero i valori di x), cioè non solo per |V(\log 1)|, |V(\log 2)|, |V(\log 3)|, \ldots. Analogamente, per calcolare \beta^{\prime} si considerano tutti i valori della funzione g(\xi) := \frac{1}{\log \xi} \int_0^{\log \xi} |V(u)|\ du per \xi \in [1, +\infty), non solo \frac{1}{\log 1} \int_0^{\log 1} |V(u)|\ du, \frac{1}{\log 2} \int_0^{\log 2} |V(u)|\ du, \frac{1}{\log 3} \int_0^{\log 3} |V(u)|\ du, \ldots. Stiamo calcolando quindi dei limiti superiori non di successioni, ma di funzioni. In uno dei nostri precedenti articoli abbiamo visto qual è l’idea che sta dietro la definizione del limite superiore di una successione, e ne abbiamo dato una definizione formale. Adesso si potrebbe fare lo stesso discorso per il limite superiore di una funzione, evidenziando le differenze rispetto al caso di una successione; tuttavia ci limiteremo solamente ad una proprietà essenziale, che ci consentirà di andare avanti e di raggiungere i nostri scopi. Questa proprietà è che, se abbiamo una funzione reale h definita su in intervallo I illimitato a destra, e consideriamo una successione ottenuta scegliendo un sottoinsieme numerabile dei valori della funzione, cioè una successione del tipo h(a_1), h(a_2), \ldots, h(a_n), \ldots, con a_1, a_2, \ldots, a_n, \ldots \in I, allora il limite superiore della funzione è maggiore o uguale del limite superiore della successione. Applicando questa proprietà al caso di \alpha^{\prime}, abbiamo che I = [1, +\infty), h(\xi) = f(\xi) = |V(\log \xi)| e scegliamo i valori della funzione ottenuti per valori interi di \xi (cioè h(a_1), h(a_2), \ldots, h(a_n), \ldots = h(1), h(2), \ldots, h(n), \ldots = |V(\log 1)|, |V(\log 2)|, \ldots, |V(\log n)|, \ldots). Secondo questa proprietà, il limite superiore della funzione f(\xi) = |V(\log \xi)| è maggiore o uguale del limite superiore della successione |V(\log 1)|, |V(\log 2)|, \ldots, |V(\log n)|, \ldots. Ma il limite superiore della funzione lo abbiamo chiamato \alpha^{\prime}, mentre il limite superiore della successione lo abbiamo chiamato \alpha, per cui:
Potete notare che in tutto ciò non abbiamo ancora detto cos’è il limite superiore di una funzione; abbiamo solo detto che esso è maggiore o uguale al limite superiore di qualsiasi successione ottenuta calcolando la funzione su un insieme numerabile di punti del suo dominio (a proposito, le successioni di questo tipo si chiamano successioni estratte). In realtà, da qui alla definizione il passo è breve, perché a questo punto si può definire il limite superiore di una funzione come il più piccolo numero reale che è maggiore o uguale dei limiti superiori di tutte le sue successioni estratte. Al momento però questa definizione ci interessa poco, perché ci basta sapere che \alpha^{\prime} \geq \alpha.
Naturalmente si può ripetere lo stesso ragionamento per \beta e \beta^{\prime}, ottenendo che:
Guardando queste proprietà dal punto di vista di \alpha e \beta, possiamo enunciare la seguente Proprietà:
Relazione tra \alpha e \alpha^{\prime}, e tra \beta e \beta^{\prime}
Con riferimento alla Definizione N.23 (Costanti \alpha^{\prime} e \beta^{\prime}):
Come per \alpha e \beta, grazie alla limitatezza della funzione |V| possiamo escludere che \alpha^{\prime} = +\infty e che \beta^{\prime} = +\infty:
\alpha^{\prime} e \beta^{\prime} sono reali
Le costanti \alpha^{\prime} e \beta^{\prime} definite dalla Definizione N.23 sono numeri reali.
La dimostrazione è praticamente la stessa del Corollario I della Proposizione N.7A.
In questo articolo dimostreremo la seguente Proposizione:
Relazione tra \alpha e \beta^{\prime}
Con riferimento alle Definizioni N.23 e N.14:
Ricordiamo che il nostro obiettivo, per il Lemma N.7, è dimostrare che \alpha = 0. Nei prossimi articoli useremo la Proposizione N.23 per dimostrarlo per assurdo: supporremo che \alpha \gt 0 e da ciò dedurremo che \beta^{\prime} \lt \alpha; ma questo è in contraddizione con la Proposizione N.23, perciò l’ipotesi che \alpha \gt 0 deve essere falsa, cioè \alpha deve essere zero (in quanto non può essere negativo, perché è il limite superiore di una funzione non negativa).
Ma perché complicare le cose con \beta^{\prime}, invece di dimostrare direttamente che \alpha = 0? In realtà, come vedremo nei prossimi articoli, è relativamente semplice dimostrare l’implicazione \alpha \gt 0 \Rightarrow \beta^{\prime} \lt \alpha, mentre nessuno finora è riuscito a dimostrare che \alpha = 0 in modo più diretto, senza ricorrere a \beta^{\prime}. L’introduzione di \beta^{\prime} è proprio una delle idee chiave dell’intera dimostrazione del Teorema dei numeri primi, non solo perché di fatto è l’unico modo che si conosce per dimostrare che \alpha = 0, ma anche perché consente di dividere la dimostrazione in due parti principali:
- La dimostrazione che \alpha \leq \beta^{\prime}: è la parte, lunga e complicata, che termina con questo articolo;
- La dimostrazione dell’implicazione \alpha \gt 0 \Rightarrow \beta^{\prime} \lt \alpha: è la parte, relativamente semplice, che tratteremo nei prossimi articoli.
Nel prossimo paragrafo vedremo la dimostrazione della Proposizione N.23.
Volendo considerare anche \alpha^{\prime} e ricordando che \alpha \leq \alpha^{\prime}, partendo dalla Proposizione N.23 si potrebbe ipotizzare che:
Oppure, ricordando che \beta \leq \beta^{\prime}, si potrebbe ipotizzare che:
Quindi, ferma restando la seconda parte della dimostrazione, ossia che \alpha \gt 0 \Rightarrow \beta^{\prime} \lt \alpha, due obiettivi alternativi per la prima parte potrebbero essere, rispettivamente, dimostrare che \alpha^{\prime} \leq \beta^{\prime}, o che \alpha \leq \beta. La prima relazione è vera, e la discuteremo nel prossimo articolo. La seconda non sappiamo è vera, ma, non essendo necessario dimostrarla per dimostrare il Teorema dei numeri primi, questo non è un grosso problema.
Si potrebbe osservare che la definizione di \beta è sostanzialmente inutile, perché le costanti di interesse sono in fin dei conti \alpha e \beta^{\prime}: sarebbe bastato definire direttamente queste ultime fin dall’inizio.
Quest’osservazione è corretta, tuttavia abbiamo introdotto in un primo momento \beta perché preferiamo sempre lavorare con i numeri interi fin quando è possibile: in questo modo si arriva a dei punti in cui, per poter continuare, è necessario passare ai numeri reali. Queste situazioni secondo noi sono molto interessanti, perché permettono di apprezzare il valore dell’analisi reale, rispondendo alla domanda che spesso alcuni si pongono: “perché per dimostrare delle cose semplici a volte è necessario utilizzare delle tecniche matematiche sofisticate?”.
La dimostrazione che \alpha \leq \beta^{\prime}
Partiamo dalla Proposizione N.12, che abbiamo dimostrato nell’articolo precedente:
Confrontiamo questa disuguaglianza con il nostro obiettivo, \alpha \leq \beta^{\prime}, che possiamo scrivere in modo più esplicito utilizzando le Definizioni N.23 e N.14:
Evidentemente, per passare dalla (1) alla (2), dobbiamo in qualche modo sostituire la funzione R con la funzione V. Come abbiamo osservato nell’articolo La media integrale e la funzione di errore assoluto R in corrispondenza della formula (11), le due funzioni sono legate dalla seguente relazione che vale per ogni u \in [0, +\infty):
Possiamo far comparire questa funzione nell’integrale al secondo membro della (1) mediante la sostituzione t := \frac{x}{e^u}:
Prima di cominciare, osserviamo che la sostituzione t := \frac{x}{e^u} è conveniente perché, effettuandola partendo dall’espressione R\left(\frac{x}{t}\right) che compare nell’integrale, si ottiene R\left(x / \frac{x}{e^u}\right) = R\left(\frac{x e^u}{x}\right) = R(e^u), che è proprio il numeratore della (3). Questa sostituzione consente quindi di passare dalla funzione R alla funzione V.
Così facendo dobbiamo però considerare che la nuova variabile di integrazione diventa u, per cui dobbiamo esprimere dt in funzione di du e ricalcolare gli estremi di integrazione:
- Da t := \frac{x}{e^u} si ottiene dt = d\left(\frac{x}{e^u}\right) = x d\left(\frac{1}{e^u}\right) = x \left(- \frac{1}{e^{2u}} d(e^u) \right) = x \left(- \frac{1}{e^{2u}} e^u du \right) = - x \frac{1}{e^{u}} du
- Se t = 1, abbiamo che \frac{x}{e^u} = t = 1. Essendo x \neq 0, possiamo dividere per x, ottenendo \frac{1}{e^u} = \frac{1}{x}. Essendo ambo i mebri diversi da zero, otteniamo e^u = x, cioè u = \log x. Quindi il nuovo estremo inferiore di integrazione sarà \log x.
- Se t = x, abbiamo che \frac{x}{e^u} = t = x, da cui \frac{1}{e^u} = 1 \Rightarrow e^u = 1 \Rightarrow u = 0. Quindi il nuovo estremo superiore di integrazione sarà 0.
Quindi abbiamo:
La costante x può essere portata fuori dall’integrale, mentre il segno meno può essere eliminato scambiando gli estremi di integrazione (in modo che l’estremo inferiore sia, come di consueto, più piccolo di quello superiore):
Combinando le due formule precedenti si ottiene il passaggio (*).
Per prima cosa osserviamo che \log x - u = \int_u^{\log x} dv. Così possiamo trasformare l’integrale di partenza in un integrale doppio:
Dato che il termine |V(u)| non dipende da v, possiamo portarlo dentro l’integrale più interno:
Ora scambiamo l’ordine di integrazione. Procederemo con un approccio intuitivo, basato sull’idea di trattare l’integrale come una sommatoria (questa idea non è molto distante dalla realtà, dato che l’integrale è definito come il limite di una sommatoria, ma richiederebbe di essere formalizzata).
L’integrale sulla destra si può leggere così: “Fai variare u tra 0 e \log x; per ogni valore di u fai variare v tra u e \log x; per ogni coppia (u, v) così ottenuta calcola |V(u)|; alla fine somma il tutto”. Concentriamoci ora sull’insieme delle possibili coppie (u, v). Abbiamo detto come generare queste coppie fissando prima un valore per u e poi un valore per v, ma se facessimo il contrario?
Abbiamo detto che v varia tra u e \log x, e con ciò intendiamo che essa assume, per ciascun valore di u, tutti i valori compresi tra u e \log x (d’ora in poi, intenderemo sempre questo quando useremo l’espressione “varia tra”). Ma u varia tra 0 e \log x, allora in particolare, se u = 0, v varia tra 0 e \log x (per valori di u maggiori di zero, v assumerà comunque valori in questo intervallo, ma non li assumerà tutti, perché il minimo valore da essa assunto sarà u \gt 0). Quest’osservazione è importante perché ci dice che, comunque scegliamo un valore c \in [0, \log x], esiste almeno una coppia (u, v) con tale valore per v: basta prendere u := 0 e v := c. Per verificarlo, basta osservare che la coppia (u, v) := (0, c) soddisfa i vincoli delle variabili di integrazione, ossia 0 \leq u \leq \log x e u \leq v \leq \log x.
Ora facciamo un passo ulteriore. Fissato un valore per la variabile v \in [0, \log u], vediamo quali sono tutti e soli i valori di u tali che esista la coppia (u, v) (posto che, come abbiamo appena visto, u = 0 è uno di questi valori). In generale, dato che v varia tra u e \log x, si deve avere che u \leq v. Questo è il massimo valore possibile per u. Il minimo è certamente 0 perché, come abbiamo visto prima, u := 0 è un valore ammissibile per qualunque valore di v, e u non può essere negativo. Quindi, fissato un valore per v, l’intervallo dei valori ammissibili per u è [0, v]: non esistono coppie del tipo (u, v) con valori di u al di fuori di questo intervallo. Allora, se consideriamo l’integrale come una somma estesa a tutte le coppie (u, v), possiamo rileggerlo in questo modo: “Fai variare v tra 0 e \log x; per ogni valore di v fai variare u tra 0 e v; per ogni coppia (u, v) così ottenuta calcola |V(u)|; alla fine somma il tutto”. Ciò corrisponde alla seguente scrittura:
Ma l’insieme delle coppie (u, v) considerate in questo modo sono le stesse di prima, perché per ogni possibile valore di v abbiamo trovato tutti e soli i corrispondenti valori di u, quindi abbiamo semplicemente esaminato le stesse coppie di prima in ordine diverso. Per questo principio (che è valido per le sommatorie, ma che per gli integrali rimane una spiegazione di tipo intuitivo), abbiamo che:
Questa formula, assieme alle precedenti, spiega il passaggio (**).
L’ultima espressione tra parentesi è formalmente molto simile all’argomento del secondo \limsup della (2); per ricollegarci a questa formula, dobbiamo appunto introdurre il \limsup. A tal proposito, dobbiamo sapere che in generale vale la seguente Proprietà:
Maggiorazione di una funzione col suo limite superiore
Sia f una funzione reale definita su un insieme illimitato superiormente. Allora:
Prima di capire perché vale questa Proprietà, ricordiamo che, per la Definizione A.9, essa significa che esiste una funzione h tale che f \leq \left( \limsup_{x \to \infty} f(x) \right) + h, e h \to 0 (dove \limsup_{x \to +\infty} f(x) è un numero reale, che in questa relazione rappresenta la funzione costante pari a quel numero).
Non dimostreremo formalmente questa Proprietà, ma possiamo capirla intuitivamente almeno nel caso delle successioni: utilizzando la terminologia dell’articolo Il limite inferiore e il limite superiore di una successione, la funzione h rappresenta quanto i valori della funzione superano il suo limite superiore (la differenza tra essi e il limite superiore deve tendere a zero perché, se così non fosse, tali valori sarebbero abbastanza per dar luogo a un limite superiore maggiore di quello effettivo, il che sarebbe assurdo).
Applicando questa Proprietà alla funzione f(v) := \frac{1}{v} \int_0^v |V(u)|\ du, possiamo continuare lo sviluppo della (4) come segue:
In quest’ultimo limite superiore, la variabile v assume tutti i valori reali compresi nell’intervallo [0, +\infty). Quindi se poniamo \xi := e^v (da cui v = \log \xi), abbiamo che \xi assume tutti i valori reali nell’intervallo [1, +\infty), proprio come la \xi della Definizione N.23; inoltre se v = \log \xi \to \infty, allora anche \xi \to \infty. Quindi:
Per cui, sostituendo nella (5), abbiamo:
dove nell’ultimo passaggio abbiamo applicato il Corollario 1 della Proprietà A.8, che si dimostra per gli o piccoli come si dimostra per gli O grandi.
Facendo un po’ di calcoli, l’ultima espressione della (6) si può semplificare come segue:
Per le proprietà degli integrali:
Sviluppiamo il primo integrale:
Il secondo integrale si sviluppa in maniera simile, ma come primo passaggio bisogna applicare la Proprietà A.15 per portare il simbolo di o piccolo fuori dall’integrale (la Proprietà citata è stata formulata per O grande, ma vale anche per o piccolo):
dove nell’ultimo passaggio abbiamo applicato la Proprietà A.8A, che è stata formulata per O grande ma vale anche per o piccolo.
Sostituendo la (b) e la (c) nella (a), abbiamo quindi che:
da cui:
La (7) segue dall’uguaglianza x o(\log^2 x) = o(x \log^2 x), conseguenza della Corollario 1 della Proprietà A.8 nel caso degli o piccoli.
In definitiva, unendo le formule (4), (5), (6) e (7), si ottiene:
Sostituendo nella (1), si ottiene:
Semplificando gli ordini asintotici, si ottiene:
Essendo x \log x = o(x \log^2 x), abbiamo che O(x \log x) = O(o(x \log^2 x)) = o(x \log^2 x), dove nell’ultima uguaglianza abbiamo applicato la Proprietà A.16. Quindi o(x \log^2 x) + O(x \log x) = o(x \log^2 x) + o(x \log^2 x) = o(x \log^2 x), dove nell’ultimo passaggio abbiamo applicato il Corollario della Proprietà A.9, che si dimostra allo stesso modo per gli o piccoli.
Quest’ultima disuguaglianza si può sviluppare come segue:
- Nel passaggio (*) abbiamo diviso tutto per \log^2 x, assumendo che x \gt 1 ed applicando la Proprietà A.8A per quanto riguarda l’o piccolo;
- Nel passaggio (**) abbiamo assunto che, se una successione è minore o uguale di un’altra, anche il suo limite superiore è minore o uguale di quello dell’altra. Non dimostreremo questa proprietà, ma la riteniamo abbastanza intuitiva.
- Nel passaggio (***) abbiamo considerato che il limite di una costante è la costante stessa e che per definizione il limite di un o(1) è zero, cioè \lim_{x \to +\infty} \beta^{\prime} = \beta^{\prime} e \lim_{x \to +\infty} o(1) = 0, per cui \lim_{x \to +\infty} \left( \beta^{\prime} + o(1) \right) = \beta^{\prime}; quindi, in base alla Proprietà A.3, anche \limsup_{x \to +\infty} \left( \beta^{\prime} + o(1) \right) = \beta^{\prime}.
Considerazioni finali
Terminiamo questo articolo con una rappresentazione grafica della relazione \alpha \leq \beta^{\prime} che abbiamo appena dimostrato. Sappiamo che si tratta di una relazione tra due limiti superiori, perché \alpha è definito come il limite superiore della funzione |V(\log x)| e \beta^{\prime} è definito come il limite superiore della funzione \frac{1}{\log \xi} \int_0^{\log \xi} |V(u)|\ du (la prima definita sugli interi positivi, la seconda sui reali maggiori o uguali di 1). Le due funzioni sono rappresentate nel seguente grafico:
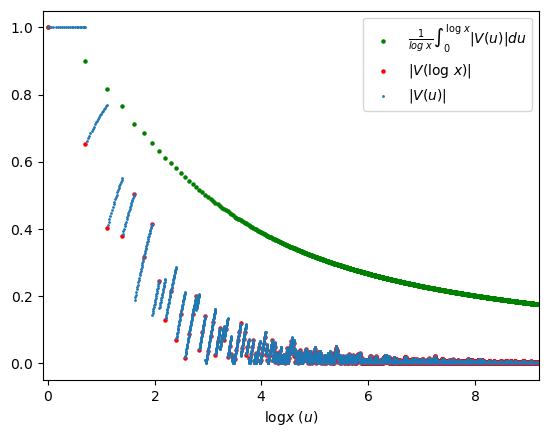
Dal grafico si vede chiaramente che la funzione |V(\log x)| tende a zero, per cui \limsup_{x \to +\infty} |V(\log x)| = \alpha = 0. Questa relazione, ricordando il Lemma N.7, in sostanza coincide con l’enunciato del Teorema dei numeri primi. Considerando i valori interi x = \xi = 1, 2, 3, \ldots, la relazione |V(\log x)| \leq \frac{1}{\log \xi} \int_0^{\log \xi} |V(u)|\ du è soddisfatta per tutti valori puntuali di x e \xi mostrati nel grafico, però bisogna considerare che la discesa della funzione \frac{1}{\log \xi} \int_0^{\log \xi} |V(u)|\ du è molto lenta, perché \log \xi cresce molto lentamente al crescere di \xi, per cui non si può escludere che esistano delle x tali che |V(\log x)| \gt \frac{1}{\log x} \int_0^{\log x} |V(u)|\ du. Comunque, anche se esistessero dei tali valori di x, ciò non sarebbe in contraddizione col fatto che \alpha \leq \beta^{\prime}; ad esempio, la successione mostrata nella Figura 3 dell’articolo Il limite inferiore e il limite superiore di una successione ha come limite superiore 1 anche se infiniti suoi valori sono maggiori di 1 (ma sempre più vicini ad esso man mano che ci si sposta verso destra nel grafico).