Prerequisiti:
- Dai numeri interi ai numeri reali
- Elementi di analisi asintotica
- Serie numeriche, serie numeriche divergenti
- Numero di Nepero (e)
- Integrali e loro proprietà
- Significato geometrico dell’integrale
La teoria dei numeri è piena di somme “notevoli” (termine che in matematica non significa “molto grandi”, ma “degne di nota”). La prima che analizziamo è la somma degli inversi dei primi numeri interi positivi:
Si tratta di una somma infinita di numeri, chiamata anche serie numerica. La teoria delle serie numeriche ci dice che questa serie, chiamata serie armonica, diverge, ossia la somma dei suoi primi n termini diventa arbitrariamente grande al crescere di n. In altri termini, possiamo fissare qualsiasi numero M e star certi che, per quanto grande sia M, calcolando nell’ordine le cosiddette somme parziali:
ad un certo punto arriveremo a superare il numero M che avevamo fissato. Questo è il comportamento asintotico della serie, ossia ciò che succede quando il numero di termini della somma tende all’infinito.
Conoscere il comportamento asintotico è importante, ma in molti casi non basta. Ad esempio, fissiamo M = 10 e supponiamo di applicare, per gioco o per esercizio, la definizione di serie divergente: supponiamo cioè di sommare nell’ordine i termini della serie, fino a superare M. Supponendo di avere a disposizione solo una classica calcolatrice, quanto pensereste di metterci? Quante somme secondo voi sarebbero necessarie? Provate ad indovinare. Probabilmente riterreste necessarie alcune decine di somme, al più poche centinaia, ed in termini di tempo non più di qualche decina di minuti. Se provaste a svolgere l’esercizio, comincereste forse con entusiasmo, ma ben presto vi accorgereste che l’impresa non è affatto semplice. Fareste decine, centinaia, migliaia di somme… arrivereste a superare 10 solo dopo aver sommato ben 12.368 termini della serie! Anche ipotizzando di fare un calcolo al secondo senza mai fermarvi, per completare l’impresa impieghereste più di tre ore.
Fortunatamente oggi abbiamo dei computer che possono svolgere questo calcolo in una frazione di secondo, ma questo esempio ci fa capire quanto povera sia la conoscenza del solo comportamento asintotico, senza avere la minima idea della velocità di crescita di una serie. Nel nostro esempio, se fossimo stati in grado di stimare la somma dei primi n termini della serie, avremmo potuto capire in anticipo che l’esercizio proposto era in realtà, più che un esercizio, una folle impresa.
Vediamo allora cosa possiamo dire sulla somma dei primi n termini della serie:
Possiamo vedere ogni termine come l’area di un rettangolo avente come altezza il termine stesso e come base 1. Ad esempio, per n = 6, la somma (2) non è altro che l’area del seguente istogramma:
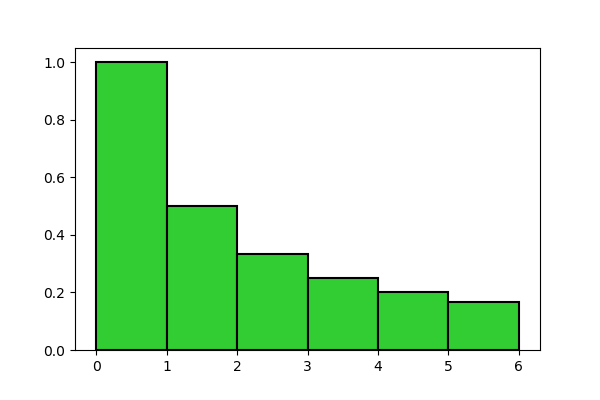
Per calcolare l’area, che indicheremo con la lettera A, possiamo applicare il Lemma dell’area dell’istogramma, nella sua seconda forma (Lemma N.5), secondo cui
Ricordiamo che, nel Lemma citato, la funzione C(n) calcola la somma delle prime n basi dell’istogramma, mentre la funzione f(n) restituisce le altezze dei singoli rettangoli; inoltre \overline{C} e \widetilde{f} sono rispettivamente l’estensione semplice di C ed un’estensione di classe C^1 di f. Vediamo quali sono queste funzioni nel nostro caso.
Essendo tutte le basi unitarie, la somma delle prime k basi è semplicemente k, per cui
La sua estensione semplice \overline{C} è la funzione mostrata nella Figura 1 dell’articolo Dai numeri interi ai numeri reali, che riportiamo qui per comodità:
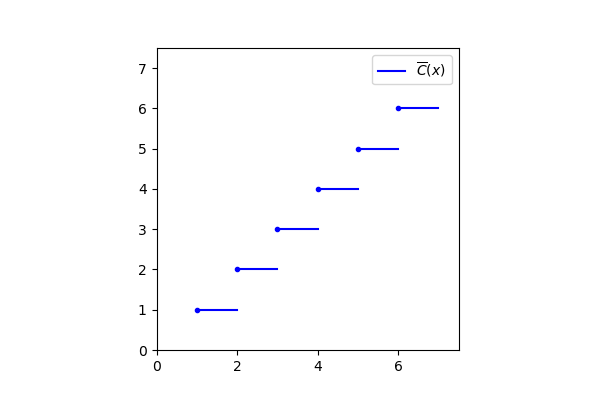
Ma questa funzione la conosciamo già: è la parte intera approssimata per difetto (o semplicemente “parte intera”):
Se volessimo dimostrarlo, dovremmo definire formalmente la parte intera e confrontarla con la definizione di estensione semplice, ma si tratterebbe di un mero esercizio formale, che possiamo trascurare. Piuttosto, è importante notare come la formula (5) sia evidente dal grafico: ad esempio la funzione \overline{C}(t) assume sempre valore 1 per tutti i numeri reali compresi tra 1 incluso e 2 escluso, che sono appunto quelli che, approssimati all’intero immediatamente precedente, sono pari ad 1.
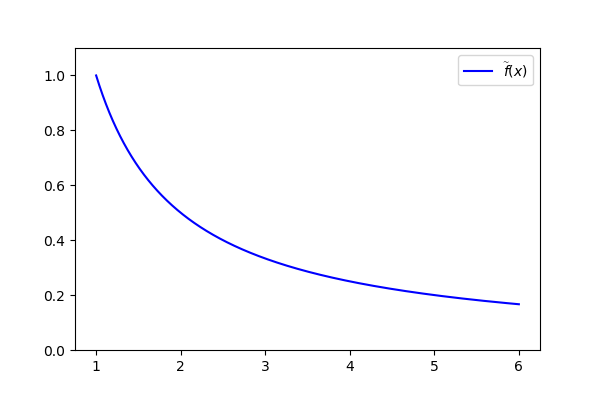
Per quanto riguarda la funzione f, quella che calcola le altezze, nel nostro caso si tratta della funzione
Come estensione scegliamo quella più “naturale”:
che possiamo vedere nell’immagine seguente:
Sostituendo le formule (4), (5), (6) e (7) nella (3), otteniamo:
Proviamo a capire meglio cosa significa questa formula. Essa calcola l’area dell’istogramma mostrato in Figura 1, ma osservando la sua formulazione possiamo notare che abbiamo scomposto quest’area in una somma, il cui primo termine è 1, e il secondo è l’integrale \int_1^n \left \lfloor t \right \rfloor \frac{1}{t^2} dt. L’1 si può identificare col primo rettangolo, che ha base 1 ed altezza 1, per cui l’integrale non può che essere pari all’area di tutti gli altri rettangoli messi insieme:
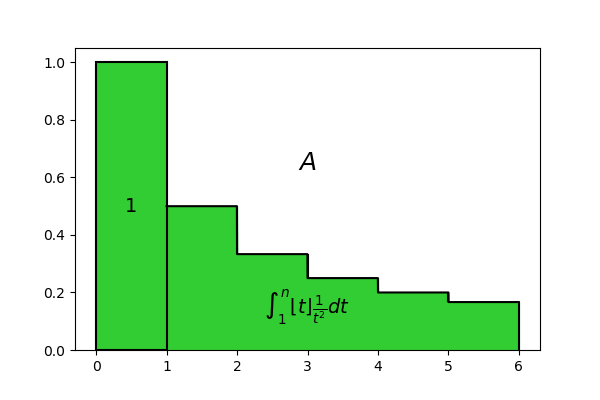
Abbiamo così calcolato l’area dell’istogramma in Figura 1, ma la formula che abbiamo trovato contiene la parte intera, che è poco gestibile con metodi analitici per via della sua non continuità. Proviamo ad eliminarla. Così facendo otteniamo l’espressione seguente, il cui risultato possiamo chiamare A^{\prime}:
Questa espressione ha un’interpretazione geometrica simile a quella della formula (8). Ricordiamo che il significato geometrico dell’integrale di una funzione continua positiva è l’area della figura ottenuta proiettando verticalmente gli estremi del grafico della funzione sull’asse orizzontale. In questo caso, se consideriamo il grafico della funzione f(t) = \frac{1}{t} tra 1 ed n e proiettiamo i punti (1, f(1)) ed (n, f(n)) sull’asse orizzontale, otteniamo una figura la cui area è pari all’integrale \int_1^n \frac{1}{t} dt. Se poi a questa figura accostiamo il nostro rettangolo di area unitaria, otteniamo una figura molto simile alla precedente, la cui area è proprio il numero A^{\prime} = 1 + \int_1^n \frac{1}{t} dt:
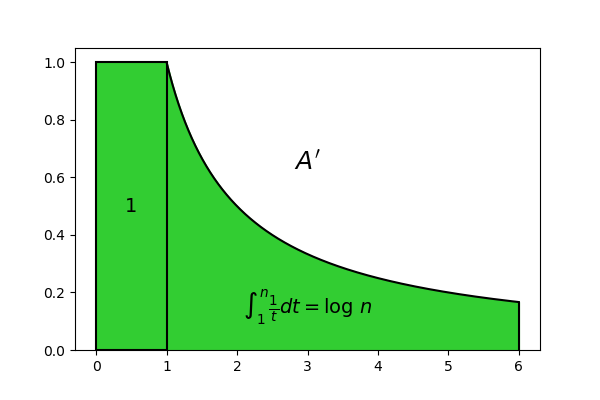
Rispetto alla Figura 4, i rettangoli dal secondo in poi sono stati sostituiti col grafico della funzione f(t) = \frac{1}{t}. Le aree delle due figure sembrano essere molto simili, tanto che possiamo considerare A^{\prime} come un’approssimazione di A. Il vantaggio è che A^{\prime} è molto più semplice da calcolare:
dove la base del logaritmo è il numero di Nepero e (ed in tal caso siamo soliti non indicarla esplicitamente, seguendo una convenzione piuttosto diffusa).
Usando A^{\prime} come approssimazione di A, possiamo scrivere quindi:
Se sovrapponiamo le Figure 4 e 5, possiamo visualizzare la differenza tra le due aree, e quindi l’errore che commettiamo con quest’approssimazione:
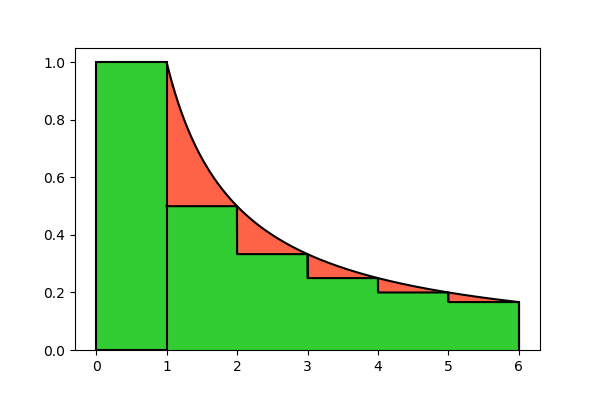
Possiamo notare che il grafico della funzione f(t) passa sempre sopra le sommità dei rettangoli, perciò A^{\prime} \gt A. Allora la (9) è un’approssimazione per eccesso. Per quantificare quanto sia in eccesso, dovremmo stimare l’area complessiva delle parti rosse, che costituiscono la differenza tra A e A^{\prime}. Considereremo quest’area negativa, perché va sottratta dalla stima A^{\prime} per ottenere il valore esatto A:
Stimare l’area delle parti rosse è più semplice di quanto possa sembrare. Infatti esse si riducono di dimensioni così rapidamente, procedendo verso destra, che non è poi così sbagliato sommarle tutte fino all’infinito, e prendere questa somma infinita come approssimazione:
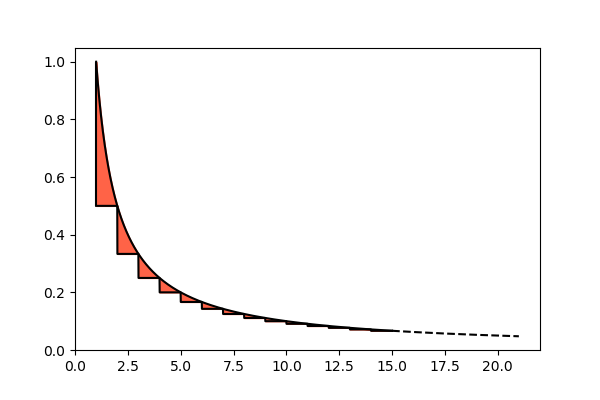
Questa figura, sebbene si estenda all’infinito verso destra, ha un’area finita. La misura di quest’area si può ottenere sperimentalmente e, approssimata alle prime due cifre decimali, vale 0,42. Possiamo quindi raffinare la nostra approssimazione come segue:
Il nuovo termine costante 0,58 che abbiamo ottenuto sottraendo 0,42 (l’area della striscia infinita delle piccole parti rosse) da 1 (l’area del primo rettangolo) è noto come costante di Eulero e viene indicato con la lettera \gamma. Perciò in definitiva possiamo scrivere
Possiamo tradurre questa formula in termini grafici come segue:
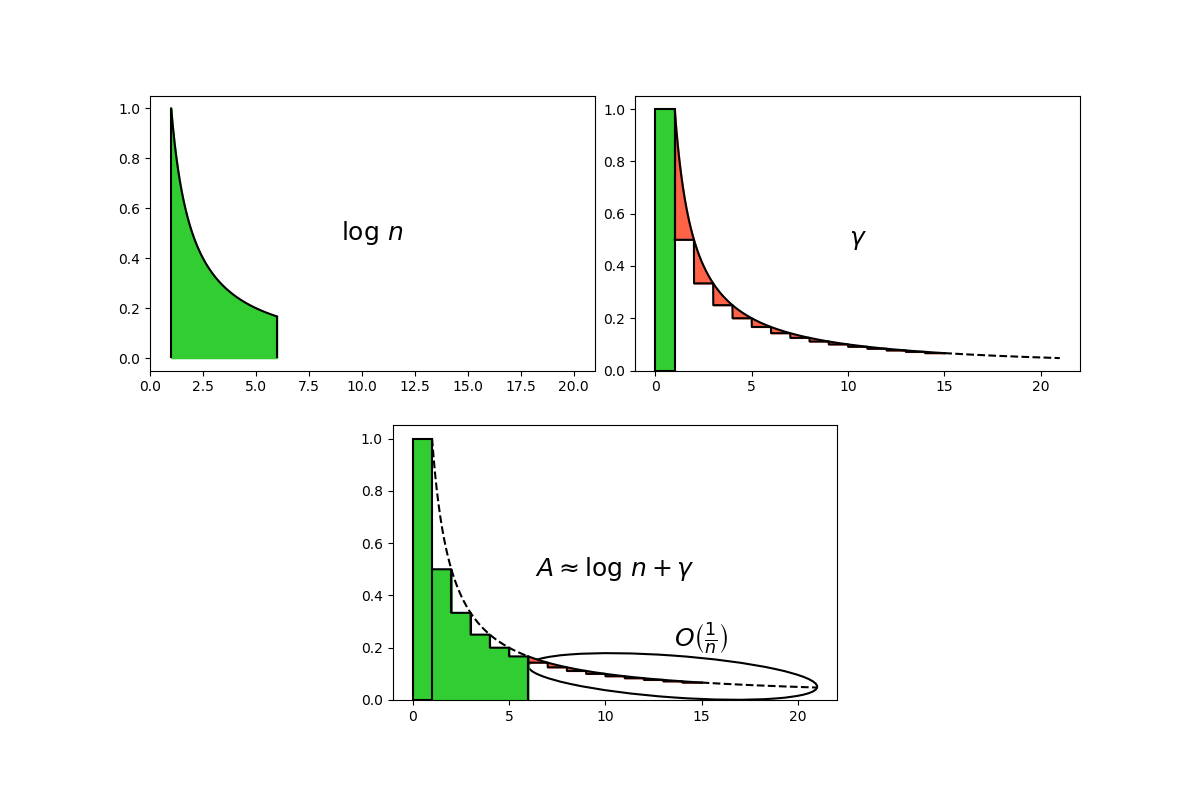
Dalla Figura 8 è evidente che si tratta di un’approssimazione per difetto, in quanto l’errore, evidenziato nell’immagine, è un’area negativa (in rosso).
Resta da capire quanto sia buona questa approssimazione. Usando gli strumenti dell’analisi asintotica, si può dimostrare che l’errore che si commette è un O grande di \frac{1}{n}, ossia, indicando con h questo errore, |h| \leq \frac{K}{n}, per qualche costante K. Il valore dell’espressione \frac{K}{n} decresce al crescere di n, per cui l’approssimazione migliora per numeri più grandi (cosa che si può intuire guardando la Figura 8: infatti, se n cresce, la striscia delle parti rosse che rappresenta l’errore diventa sempre più sottile). Tenendo conto di ciò, possiamo formulare la seguente versione asintotica della (11):
Notiamo che sia la (11) che la (12) sono formule approssimate; tuttavia mentre nella (11) l’errore è generico, nascosto nel simbolo di uguaglianza approssimata (\approx) e completamente sconosciuto, nella (12) non solo esso diventa più esplicito, ma ne conosciamo almeno l’andamento asintotico. A seconda dei casi, adotteremo entrambe le forme come nostra approssimazione dell’area dell’istogramma:
Approssimazione della somma degli inversi dei primi numeri interi positivi
Per ogni intero n \gt 0:
dove la base del logaritmo è il numero di Nepero e, mentre \gamma \approx 0,58 è la costante di Eulero. In particolare:
In aggiunta a quanto detto sopra, restano da dimostrare due cose:
- Che la Figura 7, la striscia infinita delle parti rosse, ha un’area finita
- Che l’errore dell’approssimazione (11) è asintoticamente O(\frac{1}{n})
Cominciamo ad esprimere con una formula l’area della Figura 7. Per fare ciò, partiamo dall’area delle parti rosse della Figura 6. Come si può vedere facilmente confrontando le Figure 4 e 5, quest’area è data da:
Facendo tendere n all’infinito, abbiamo che l’area della Figura 7 è data da:
Ma ogni numero reale t differisce dalla sua parte intera di meno di un’unità, cioè t - \left \lfloor t \right \rfloor \lt 1. Ciò consente di maggiorare l’integrale come segue (tenendo conto che quando il segno di \lt “passa fuori” dall’integrale, in generale diventa \leq):
Questo integrale converge, perché la serie associata \sum_{n=1}^{\infty} \frac{1}{n^2} converge (supponiamo che abbiate familiarità con questo principio, ma in uno dei prossimi articoli ne parleremo dal punto di vista della teoria dei numeri). Ciò significa che la Figura 7 ha un’area finita: abbiamo completato il primo punto.
Per quanto riguarda l’errore dell’approssimazione (11), confrontando le Figure 6, 7 e 8, si vede che esso è dato dall’area di quella parte della Figura 7 che si trova sulla destra dell’ultimo rettangolo dell’istogramma. In formule:
L’errore che si commette con l’approssimazione (11) è quindi esattamente \int_n^{\infty} \frac{t - \left \lfloor t \right \rfloor}{t^2} dt, quantità che indicheremo con h_n per evidenziare il fatto che dipende solo da n. Vediamo come si comporta asintoticamente questo errore, al crescere di n. Possiamo applicare la stessa idea del passaggio (15): essendo, per ogni t, 0 \leq t - \left \lfloor t \right \rfloor \lt 1, abbiamo che
L’integrale sulla destra si può calcolare in maniera esatta:
Dunque la (16) si può riscrivere come segue:
Per cui a maggior ragione h_n = O\left(\frac{1}{n}\right), come volevamo dimostrare.
In alternativa, chi è più familiare con le relazioni asintotiche potrebbe procedere in modo più veloce come segue:
Tuttavia il passaggio di O(1) fuori dall’integrale è una proprietà che andrebbe dimostrata e potrebbe dar luogo ad errori se non applicata correttamente, perciò consigliamo questo modo di procedere solo ai più esperti.
Come abbiamo osservato nell’articolo sul Teorema di Chebyshev, i logaritmi hanno un’importanza fondamentale nella teoria dei numeri. Il Teorema N.6 ne è un’ulteriore conferma, in quanto esso costituisce uno dei mattoni fondamentali di tutta la costruzione che vedremo nei prossimi articoli e che ci porterà fino al Teorema di numeri primi.
Ma il Teorema N.6 riveste grande importanza anche per un’altra ragione: è qui che compare per la prima volta il logaritmo naturale, ossia quello avente come base il numero di Nepero e. Questo tipo di logaritmo lo ritroveremo quasi sempre, da qui in poi. Saranno pochi i teoremi dove la base del logaritmo è ininfluente, come il Teorema di Chebyshev. Nella maggior parte dei Teoremi il logaritmo sarà in base e, perché uno degli anelli della catena di ragionamenti che ci condurranno ad essi, sarà proprio il Teorema N.6.
Proviamo ad usare l’approssimazione del Teorema N.6 per risolvere l'”esercizio” proposto inizialmente, ossia calcolare il numero di termini della serie (1) che bisogna sommare per arrivare almeno a 10. Cerchiamo quindi il più piccolo n tale che:
Possiamo usare l’approssimazione (13) trasformando questa disuguaglianza in:
Facendo un po’ di conti, si ottiene:
Quindi, secondo la nostra stima, per raggiungere una somma di 10, n deve essere almeno 12.406. Osserviamo che si tratta di una stima per eccesso, essendo il numero corretto 12.368. Si potrebbe obiettare: “ma non abbiamo detto che la stima era per difetto?”. In realtà la stima dell’area dell’istogramma, ossia la stima della somma della serie, è per difetto, ma proprio perché la somma della serie è sottostimata, sono necessari, secondo la stima, più termini del necessario per arrivare ad un numero prefissato, in questo caso 10. Comunque, al di là del fatto che la stima di n sia per eccesso, il valore ottenuto è molto vicino a quello reale: l’errore che abbiamo commesso è di circa lo 0,3%, ed esso può essere ulteriormente ridotto usando più cifre decimali della costante \gamma (noi abbiamo considerato per semplicità solo due cifre decimali).