Prerequisiti:
In questo articolo vedremo come si arriva alla formula per il calcolo della funzione \mathrm{t\_spazio} per i tratteggi lineari di secondo ordine. Come abbiamo già fatto per le funzioni \mathrm{t} e \mathrm{t\_valore}, l’approccio generale che seguiremo sarà quello del downcast. Nel caso di \mathrm{t\_spazio}, questo approccio risulta più semplice, essendo la funzione down-conservativa (v. Proprietà T.6 (Down-conservatività delle funzioni \mathrm{t}, \mathrm{t\_valore} e \mathrm{t\_spazio})). Infatti, considerato l’x-esimo spazio di un tratteggio lineare T di secondo ordine, sappiamo che esso sarà anche uno spazio di qualsiasi sottotratteggio di primo ordine T[i], quindi esiste sempre, qualunque sia x, un intero y tale che
Il membro di destra, riferito ad un tratteggio di primo ordine, può essere calcolato con la formula del Teorema T.1, quindi il problema principale del calcolo di \mathrm{t\_spazio}_T(x) sta nel trovare il numero y. Prima di trovarlo, lo caratterizzeremo, esprimendolo come soluzione di un’equazione, in modo simile a come abbiamo fatto per il primo ordine nella Proposizione T.3 (Equazione caratteristica di \mathrm{t\_spazio} lineare di primo ordine). Vedremo però che il passaggio dalla caratterizzazione alla formula vera e propria non è facile, e per riuscirci ci converrà trovare prima una formula approssimata, che poi modificheremo in modo opportuno per arrivare alla formula esatta.
Equazione caratteristica di \mathrm{t\_spazio} lineare di secondo ordine
Siano T = (n_1, n_2) un tratteggio lineare di secondo ordine, x un intero positivo fissato, ed s := \mathrm{t\_spazio}_T(x). Allora:
- Essendo s l’x-esimo spazio di T, le prime s colonne di T si possono dividere in x spazi ed s - x colonne contenenti almeno un trattino
- Tra le s - x colonne contenenti almeno un trattino, solo quelle divisibili sia per n_1 che per n_2, cioè quelle divisibili per \mathrm{mcm}(n_1, n_2), contengono due trattini; le altre ne contengono uno solo.
Chiediamoci ora: quanti trattini sono presenti nelle prime s colonne di T? Per rispondere a questa domanda, è possibile contare i trattini in almeno due modi: per colonne e per righe.
- Se contiamo i trattini per colonne, dobbiamo contare 1 per tutte le colonne che contengono un solo trattino, e 2 per quelle che ne contengono due (più di due non è possibile, perché il tratteggio è di secondo ordine).
- Se invece contiamo i trattini per righe, dobbiamo sommare il numero di trattini presenti sulla prima riga col numero di quelli presenti sulla seconda riga, in entrambi i casi limitandoci a quelli di valore minore o uguale di s. Possiamo calcolare questi numeri applicando la Proposizione T.2 (Conteggio dei trattini fino a un certo valore in un tratteggio lineare di primo ordine).
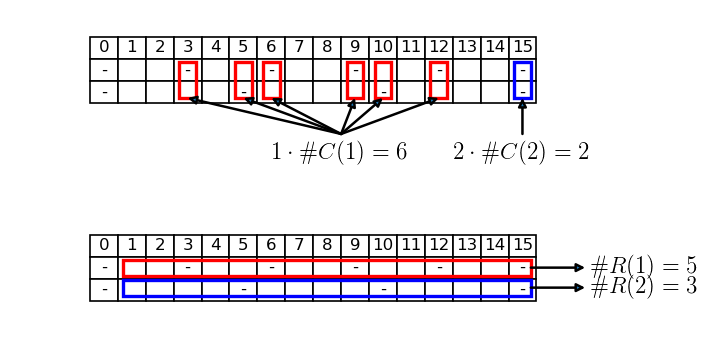
Facendo un po’ di conti, si ottengono così due formule diverse che però, siccome calcolano la stessa quantità di trattini, possono essere uguagliate, dando origine alla seguente equazione:
Indichiamo con \#C(i) il numero di colonne che contengono i trattini, per i = 1,2. Allora, contando i trattini per colonne, il loro numero totale, che chiameremo \#t, è dato dalla formula:
Possiamo osservare che \#C(1) + \#C(2) è il numero di colonne contenenti almeno un trattino, perché in un tratteggio di secondo ordine, se una colonna contiene almeno un trattino, o ne contiene o uno solo (e quindi viene contata in \#C(1)), o ne contiene due (e quindi viene contata in \#C(2)). Ma abbiamo detto che il numero di colonne contenenti almeno un trattino è s - x, per cui
Sostituendo la (2) nella (1), abbiamo che
Resta da capire come calcolare \#C(2). Se una colonna contiene due trattini, vuol dire che è divisibile sia per n_1 che per n_2, quindi è divisibile per \mathrm{mcm}(n_1, n_2). Viceversa, tutti i multipli di \mathrm{mcm}(n_1, n_2) sono divisibili per n_1 e per n_2, quindi sono colonne che contengono due trattini. Perciò i concetti di “colonna con due trattini” e “multiplo di \mathrm{mcm}(n_1, n_2)” coincidono perfettamente. Allora \#C(2) è pari al numero di multipli di \mathrm{mcm}(n_1, n_2) minori o uguali ad s, che possiamo pensare come il numero di trattini del tratteggio (\mathrm{mcm}(n_1, n_2)) aventi valore minore o uguale ad s. Questo a sua volta, per la Proposizione T.2 (Conteggio dei trattini fino a un certo valore in un tratteggio lineare di primo ordine), è dato dalla formula \left \lfloor \frac{s}{\mathrm{mcm}(n_1, n_2)} \right \rfloor:
Sostituendo nella (3) abbiamo:
Vediamo cosa succede se invece contiamo i trattini per righe. Indichiamo con \#R(i) il numero di trattini presenti sulla riga i, aventi valore minore o uguale ad s. Come abbiamo detto, possiamo calcolare questo numero applicando la Proposizione T.2, per cui il numero totale di trattini è
Contando i trattini in modi diversi, abbiamo ottenuto formule diverse; ma, dato che abbiamo contato sempre la stessa quantità di trattini, che abbiamo chiamato \#t, le due formule devono coincidere. Allora, unendo le formule (4) e (5), si ottiene la formula (6).
Come abbiamo osservato a proposito dei tratteggi di primo ordine, nel conteggio dei trattini per riga è possibile fermarsi alla colonna s - 1 anziché alla colonna s, perché quest’ultima è per ipotesi uno spazio. In altri termini, applicando la Proposizione T.2 ed il suo Corollario, abbiamo che
La condizione (7) a sua volta è esprimibile dicendo che s è uno spazio di T:
Caratterizzazione degli spazi di un tratteggio lineare di secondo ordine mediante un sistema di equazioni con la parte intera
Sia T = (n_1, n_2) un tratteggio lineare di secondo ordine. Per ogni intero positivo s vale la seguente equivalenza:
Questa Proposizione è una semplice estensione della Proposizione T.5 (Caratterizzazione degli spazi di un tratteggio lineare di primo ordine mediante un’equazione con la parte intera), secondo cui la prima equazione equivale a dire che s è uno spazio del tratteggio di primo ordine (n_1), ed analogamente la seconda equazione equivale a dire che s è uno spazio di (n_2). Quindi
In altri termini, s non è divisibile né per n_1 (perché è uno spazio di (n_1)), né per n_2 (perché è uno spazio di (n_2)). Ma questo significa che s è uno spazio di T = (n_1, n_2).
Unendo la formula (6), dove per facilità di lettura portiamo tutte le parti intere sulla destra, con la condizione che s sia uno spazio di T, che abbiamo caratterizzato nella Proposizione precedente, si ottiene la cosiddetta equazione caratteristica di \mathrm{t\_spazio} lineare di secondo ordine:
Equazione caratteristica di \mathrm{t\_spazio} lineare di secondo ordine
Sia T = (n_1, n_2) un tratteggio lineare di secondo ordine. Allora
La formula (8) è detta equazione caratteristica di \mathrm{t\_spazio} lineare di secondo ordine
Per semplicità chiamiamo “equazione” la formula (8) anche se si tratta, in realtà, di un’equazione unita ad un vincolo sulle sue soluzioni.
Conteggio degli spazi in un periodo di un tratteggio lineare di secondo ordine
Prima di vedere la formula per il calcolo di \mathrm{t\_spazio}, fermiamoci un attimo per rispondere alla seguente domanda che ci porremo spesso nel seguito: “in un periodo di un tratteggio lineare di secondo ordine, quanti spazi ci sono?”.
Innanzitutto questa domanda ha senso perché, per il Corollario della Proprietà T.3 (Numero di spazi di un periodo), tutti i periodi di un tratteggio periodico hanno lo stesso numero di spazi, ed i tratteggi lineari sono periodici, per la Proprietà T.4. Possiamo dire, in altri termini, che la risposta alla domanda non dipende dal periodo che si sceglie, ma solo dal tratteggio. Dato che questo numero comparirà spesso nel seguito, conviene dargli un nome:
Numero di spazi in un periodo di un tratteggio periodico
Sia T un tratteggio periodico. Il numero di spazi in un periodo di T si denota col simbolo S(T).
Se T è un tratteggio lineare di secondo ordine, il numero S(T) è dato dalla seguente Proprietà:
Calcolo del numero di spazi in un periodo di un tratteggio lineare di secondo ordine
Sia T = (n_1, n_2) un tratteggio lineare di secondo ordine. Allora il numero di spazi presenti in un periodo di T è
Inoltre, il numero delle rimanenti colonne che non sono spazi è dato dalla formula:
Nella Proprietà T.7, oltre alla formula che calcola il numero di spazi, è presentata anche quella che calcola il numero di colonne che non sono spazi. Quest’ultimo tuttavia potrebbe essere ricavato sottraendo il numero di spazi dalla lunghezza totale del periodo, che come sappiamo è \mathrm{mcm}(n_1, n_2). Perché allora presentare due formule? Questa scelta è motivata da due fattori:
- La formula che calcola il numero di colonne che non sono spazi è più semplice da calcolare, tanto che potrebbe convenire partire da questa per calcolare S(T):
S(T) = \mathrm{mcm}(n_1, n_2) - (\mathrm{mcm}(n_1, n_2) - S(T)) = \mathrm{mcm}(n_1, n_2) - \left( \frac{n_1 + n_2}{\mathrm{MCD}(n_1, n_2)} - 1 \right)
- La dimostrazione (Teoria dei tratteggi, pagg. 122-123) risulta più semplice se si dimostra prima la (10) e poi la (9)
Osserviamo infine che, se le componenti del tratteggio sono coprime, la formula per S(T) si semplifica parecchio:
Formula approssimata per il calcolo di \mathrm{t\_spazio} lineare di secondo ordine
Se si prova a calcolare la funzione \mathrm{t\_spazio} risolvendo l’equazione caratteristica (8), ben presto ci si accorge che il termine che crea maggiori problemi nei calcoli è - \left \lfloor \frac{s}{\mathrm{mcm}(n_1, n_2)} \right \rfloor. Comunque, questo termine è il più piccolo in valore assoluto tra quelli con la parte intera, essendo quello che ha il denominatore più grande. Perciò in prima battuta possiamo pensare di trascurarlo, ottenendo così l’equazione:
L’incognita è sempre s, che ora non sarà \mathrm{t\_spazio}_T(x), ma qualcosa di simile, come andiamo a precisare col seguente Teorema:
Soluzione dell’equazione caratteristica modificata di \mathrm{t\_spazio} lineare di secondo ordine
Sia T = (n_1, n_2) un tratteggio lineare di secondo ordine diverso da (2, 2), sia x \gt 0 un intero fissato. Consideriamo la seguente equazione, ottenuta modificando l’equazione caratteristica (8), nell’incognita s:
Allora si possono verificare due casi:
- Se x è del tipo k (S(T) - 1) + 1 (per il calcolo di S(T) si veda la Proprietà T.7), con k \gt 0, allora l’equazione (8′) ammette due soluzioni, date da
k \cdot \mathrm{mcm}(n_1, n_2) \pm 1
- Altrimenti, l’equazione (8′) ammette una sola soluzione. In tal caso, si scelgano i e j tali che \{i, j\} = \{1, 2\}, e si definisca la funzione s^{\prime}_{i}: \mathbb{N}^{\star} \rightarrow \mathbb{N} come
s^{\prime}_i (x) := \left \lfloor \frac{(n_i - 1)(n_j x - 1) - 1}{(n_i - 1)(n_j - 1) - 1} \right \rfloor
Allora la soluzione della (8′) è data da \mathrm{t\_spazio}_T^{\prime}(x), dove la funzione \mathrm{t\_spazio}_T^{\prime}: \mathbb{N}^{\star} \rightarrow \mathbb{N} è definita come
\mathrm{t\_spazio}_T^{\prime}(x) := \mathrm{t\_spazio}_{(n_i)} \left( s^{\prime}_{i}(x) \right) \tag{11}e la funzione così definita è la stessa per entrambe le possibili scelte di i.
Infine, nel primo caso l’equazione (11) fornisce il valore della soluzione più grande delle due esistenti.
Si può notare che la definizione (11) somiglia molto ad un downcast, perché fa ricorso alla funzione di primo ordine \mathrm{t\_spazio}_{(n_i)}. In questo caso però non possiamo parlare in senso stretto di downcast, perché la funzione calcolata con la (11) non è la funzione \mathrm{t\_spazio} di secondo ordine, ma una sua approssimazione.
Tuttavia, vi è una notevole somiglianza formale tra la formula (11) e quella del downcast di \mathrm{t\_spazio} di secondo ordine. Mediante l’approccio del downcast, infatti, calcoliamo la funzione \mathrm{t\_spazio}_T mediante una formula del tipo
dove s_{i}(x) è una funzione di downcast di \mathrm{t\_spazio} da T a T[i]. Confrontando la (11′) con la (11), si può notare che la funzione di downcast esatta s_{i}(x) è stata sostituita con la funzione s^{\prime}_{i}(x), che è una sua approssimazione, generando così un’approssimazione nel risultato, che diventa una nuova funzione chiamata \mathrm{t\_spazio}_T^{\prime}(x) invece di \mathrm{t\_spazio}_T(x).
È interessante notare che, nel fare questa approssimazione, non si è persa la simmetria: come la formula (11′) vale per qualunque scelta di i, generando due diverse formule che calcolano \mathrm{t\_spazio}_T(x), una per i = 1 ed una per i = 2, allo stesso modo la formula (11) definisce la funzione \mathrm{t\_spazio}_T^{\prime} in due modi diversi a seconda della scelta di i, ma la funzione definita nei due casi è la stessa. Questa proprietà deriva dal fatto che l’equazione (8′), da cui si ottiene \mathrm{t\_spazio}^{\prime}_T, è simmetrica rispetto alle variabili n_1 ed n_2 proprio come la (8), da cui si ottiene \mathrm{t\_spazio}_T. Questa simmetria dell’equazione originale fa sì che, se dimostriamo che vale una formula per calcolare \mathrm{t\_spazio}_T o \mathrm{t\_spazio}^{\prime}_T, automaticamente vale la formula ottenuta da essa scambiando n_1 ed n_2. Infatti, se n_1 ed n_2 possono essere scambiati nell’equazione di partenza, senza cambiarla, essi possono essere scambiati anche nella formula che esprime la soluzione, senza cambiare il risultato.
La dimostrazione è abbastanza complicata e si trova in Teoria dei tratteggi, pagg. 208-220. Tuttavia, più che la dimostrazione, che è molto tecnica, la cosa importante è capire il senso dell’enunciato. Innanzitutto la funzione \mathrm{t\_spazio}_T^{\prime} è di un certo interesse, perché si tratta di un “generatore di spazi”. Infatti il Teorema T.12 afferma che il risultato della formula (11) è uno spazio, essendo soluzione dell’equazione (8′) che, come la (8), ammette come soluzioni solamente spazi. Un’altra caratteristica interessante della funzione \mathrm{t\_spazio}_T^{\prime} è che essa genera spazi in modo ordinato, essendo una funzione crescente in x.
In realtà non è difficile trovare funzioni con queste caratteristiche: degli esempi molto semplici sono le funzioni \mathrm{mcm}(n_1, n_2) \cdot x - 1 e \mathrm{mcm}(n_1, n_2) \cdot x + 1, che restituiscono spazi per ogni x e sono crescenti in x. Tuttavia queste formule generano un numero molto esiguo di spazi, solamente uno per ciascun periodo del tratteggio, su S(T) spazi totali. Ad esempio, considerando il tratteggio T = (3, 5), l’unico valore assunto dalla prima funzione nel periodo che va dalla colonna 0 alla colonna \mathrm{mcm}(n_1, n_2) - 1 = 14 è proprio \mathrm{mcm}(n_1, n_2) - 1 = 14, mentre in questo periodo, come in qualsiasi periodo, vi sono 8 spazi (lo verificheremo coi calcoli nell’esempio seguente). Il pregio della funzione \mathrm{t\_spazio}_T^{\prime} è quello di generare, invece, molti spazi: essa genera S(T) - 1 spazi per ogni periodo, saltandone uno solo. Illustriamo con un esempio questo comportamento, che è una conseguenza del Teorema T.12 e che per il momento non dimostriamo.
Consideriamo il tratteggio T = (n_1, n_2) = (3, 5). Per la Proprietà T.7, il numero di spazi in un periodo del tratteggio è S(T) = \frac{(n_1 - 1)(n_2 - 1) - 1}{\mathrm{MCD}(n_1, n_2)} + 1 = \frac{2 \cdot 4 - 1}{1} + 1 = 7 + 1 = 8. La funzione \mathrm{t\_spazio}_T^{\prime}(x) per questo tratteggio è la seguente:
I primi 15 valori assunti da questa funzione, per x = 1, 2, 3, \ldots, sono i seguenti:
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| \mathrm{t\_spazio}_{(n_1,n_2)}^{\prime}(x) | 1 | 2 | 4 | 7 | 8 | 11 | 13 | 16 | 17 | 19 | 22 | 23 | 26 | 28 | 31 |
Il Teorema T.12 afferma che, per ciascuna x, il numero s := \mathrm{t\_spazio}_{(n_1,n_2)}^{\prime}(x) è soluzione dell’equazione (8′), che nel nostro caso è
Ad esempio, sostituendo la coppia (x, s) = (8, 16) evidenziata in grassetto nella tabella, abbiamo:
In effetti l’equazione è soddisfatta, essendo \left \lfloor \frac{16}{3} \right \rfloor + \left \lfloor \frac{16}{5} \right \rfloor = 5 + 3 = 8 = 16 - 8, ed essendo 16 non divisibile né per 3, né per 5. La stessa cosa vale per le altre coppie della tabella.
Rappresentando graficamente queste coppie (x, s) assieme al tratteggio, possiamo vedere come in ciascun periodo tutti gli spazi, tranne l’ultimo, siano valori assunti dalla funzione \mathrm{t\_spazio}_{(n_1,n_2)}^{\prime}, ossia degli “s“. In altri termini, la funzione “salta” tutti gli spazi del tipo \mathrm{mcm}(n_1, n_2) \cdot k - 1 = 15 k - 1:
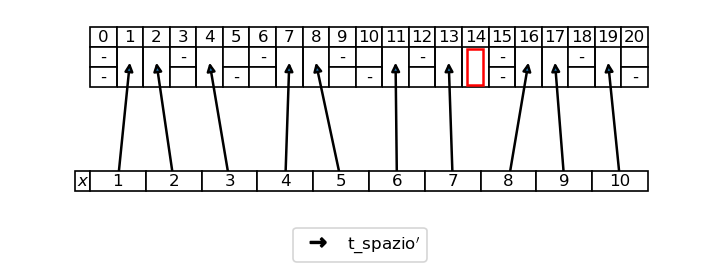
I valori di x più interessanti sono quelli che rientrano nel primo caso del Teorema T.12, ossia quelli del tipo k (S(T) - 1) + 1, con k \gt 0: la prima di queste x è S(T) e le successive sono 2 \cdot S(T) - 1, 3 \cdot S(T) - 2, eccetera. Soffermiamoci sulla prima, ottenuta con k = 1, che nel nostro caso è 8. La Proposizione citata ci dice che, per x = 8, l’equazione (8′) ha due soluzioni, che sono
Il 16 lo abbiamo visto prima: è uno dei valori assunti dalla funzione \mathrm{t\_spazio}_{(n_1,n_2)}^{\prime}, ed abbiamo verificato che soddisfa l’equazione (8′), che nel nostro caso è la (12). La stessa equazione è soddisfatta però anche dall’altro numero:
Abbiamo che \left \lfloor \frac{14}{3} \right \rfloor + \left \lfloor \frac{14}{5} \right \rfloor = 4 + 2 = 6 = 14 - 8, ed anche 14 è uno spazio del tratteggio, per cui anche 14 è una soluzione dell’equazione. Il Teorema T.12 ci dice che questi casi, in cui l’equazione ha una doppia soluzione, si verificano solo quando x è del tipo k (S(T) - 1) + 1, con k \gt 0; inoltre, quando ciò accade, la soluzione è data dalla formula (13), molto più semplice di quella che esprime \mathrm{t\_spazio}_{(n_1,n_2)}^{\prime}(x). Tuttavia, anche in questi casi la formula di \mathrm{t\_spazio}_{(n_1,n_2)}^{\prime}(x) non sbaglia, ma semplicemente “sceglie” una delle due soluzioni, quella più grande. Infatti, come abbiamo visto, \mathrm{t\_spazio}_{(3,5)}^{\prime}(8) = 16 e non 14.
Si può notare che nell’enunciato del Teorema T.12 è stato escluso il tratteggio (2,2). Infatti, se fosse n_1 = n_2 = 2, il denominatore della frazione che compare nell’espressione di s^{\prime}_i sarebbe zero, per cui questa funzione non sarebbe definita, e lo stesso varrebbe per \mathrm{t\_spazio}^{\prime}, che è definito attraverso s^{\prime}_i.
Alla luce dell’esempio precedente, il motivo dell’esclusione del tratteggio (2,2) appare più chiaro. Innanzitutto questo tratteggio può essere considerato degenere, perché ha due componenti uguali, e per lo stesso motivo è poco utile in pratica, ma a livello teorico è un caso possibile. Esso ha periodi di lunghezza 2, aventi ciascuno un solo spazio. Quindi, dato che la funzione \mathrm{t\_spazio}^{\prime} salta uno spazio per ogni periodo, essa non potrebbe mai restituire gli spazi di questo tratteggio. Affinché la funzione \mathrm{t\_spazio}^{\prime} sia applicabile, devono esserci almeno due spazi per periodo, in modo che, saltato uno spazio, ne resti almeno un altro da calcolare. Questo si verifica in tutti i tratteggi lineari di secondo ordine tranne, appunto, il tratteggio (2,2). Questa spiegazione completa quella precedente, puramente algebrica.
Formula esatta per il calcolo di \mathrm{t\_spazio} lineare di secondo ordine
Ora che abbiamo visto nel dettaglio la funzione \mathrm{t\_spazio}^{\prime}, che alla luce dell’esempio precedente possiamo considerare a tutti gli effetti una funzione \mathrm{t\_spazio} “approssimata”, grazie ad un artificio tecnico possiamo costruire la funzione esatta. I dettagli matematici sono in Teoria dei tratteggi, pagg. 221-224, ed il risultato finale è il seguente:
Downcast di \mathrm{t\_spazio} lineare dal secondo ordine al primo
Sia T = (n_1, n_2) un tratteggio lineare di secondo ordine, siano i e j tali che \{i, j\} = \{1, 2\}. Allora una funzione di downcast di \mathrm{t\_spazio} da T a T[i] è la funzione s_i: \mathbb{N}^{\star} \rightarrow \mathbb{N}^{\star} tale che:
dove S(T) è il numero di spazi in un periodo di T (v. Proprietà T.7), ed s^{\prime}_i è la funzione definita nel Teorema T.12.
Nella definizione (14) compaiono due casi:
- Il primo caso si applica quando x è multiplo di S(T), ossia x = S(T), 2 \cdot S(T), 3 \cdot S(T), \ldots. Ma, dato che ogni periodo di T ha S(T) spazi, l’S(T)-esimo spazio è l’ultimo spazio del primo periodo, il 2 \cdot S(T)-esimo spazio è l’ultimo del secondo periodo, eccetera. Questo caso quindi serve per calcolare l’ultimo spazio di ciascun periodo. Non a caso, questi spazi sono esattamente quelli che vengono “saltati” dalla funzione \mathrm{t\_spazio}^{\prime}, come abbiamo visto nell’esempio precedente.
- Nel secondo caso abbiamo che s_i(x) = s^{\prime}_i \left (x - \left \lfloor \frac{x}{S(T)} \right \rfloor \right ), ossia la funzione di downcast s_i utilizza la sua approssimata, introducendo però nell’argomento di quest’ultima il termine - \frac{x}{S(T)}, che è una “correzione” per tener conto degli spazi saltati.
Per capire meglio la definizione (14), conviene innanzitutto schematizzarla identificando tre principali funzioni in gioco:
- La funzione che ad x associa \frac{x}{S(T)} (n_i - 1) \frac{\mathrm{mcm}(n_i, n_j)}{n_i}, che si applica nel primo caso e che chiameremo f_i
- La funzione che ad x associa x - \left \lfloor \frac{x}{S(T)} \right \rfloor , che chiameremo g
- La funzione s^{\prime}_i
Così la formula (14) diventa:
Il ruolo delle funzioni f_i, g ed s^{\prime}_i, è chiarito dal seguente esempio.
Riprendiamo il tratteggio T = (3, 5) dell’esempio precedente, avente S(T) = 8. Applicando la definizione (14′) con i = 1, calcoliamo la funzione s_1(x) per x = 1, \ldots, 11:
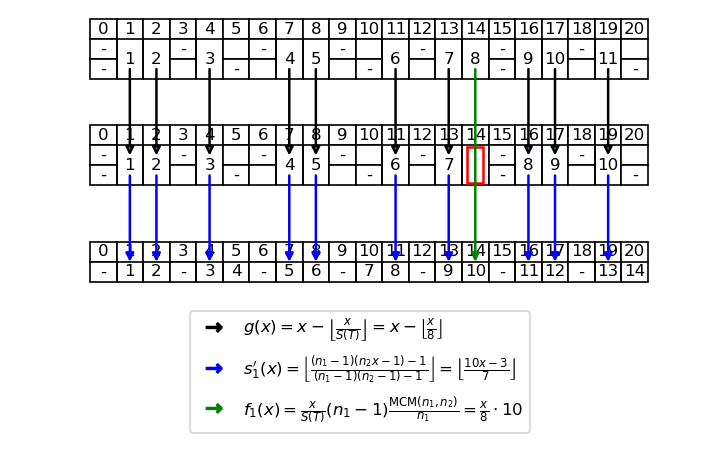
Possiamo notare come lo scopo della funzione g sia quello di trasformare l’ordinale x relativo al tratteggio T nel corrispondente argomento della funzione s^{\prime}_1, tenendo conto che questa “salta” uno spazio ogni S(T), in questo caso uno spazio ogni 8. In questo modo si può fare il downcast per tutti gli spazi che non sono gli ultimi di un periodo. Per gli altri spazi, il corrispondente ordinale del primo ordine viene calcolato in un solo passaggio mediante la funzione f_1 (ad esempio, nella Figura 3 si passa direttamente dall’ordinale 8 all’ordinale 10). Infatti, esso non potrebbe mai essere ottenuto applicando la funzione s^{\prime}_1, perché non fa parte della sua immagine (che sono i numeri “raggiunti” dalle frecce blu).
Partendo dal Teorema T.13, possiamo ottenere una formula esplicita per calcolare la funzione \mathrm{t\_spazio} di secondo ordine:
Formule per il calcolo di \mathrm{t\_spazio} lineare di secondo ordine
Sia T = (n_1, n_2) un tratteggio lineare di secondo ordine, siano i e j tali che \{i, j\} = \{1, 2\}. Allora:
dove S(T) è il numero di spazi in un periodo di T (v. Proprietà T.7).
La formula esplicita per la funzione \mathrm{t\_spazio} di secondo ordine si ottiene dall’equazione del downcast (11′), dove la funzione \mathrm{t\_spazio}_{(n_i)} è data dal Teorema T.1 e la funzione s_i è data dal Teorema T.13, che a sua volta fa riferimento al Teorema T.12. Si tratta quindi di una semplice sostituzione di una formula nell’altra, che tuttavia vale la pena analizzare nel primo caso, quando S(T) \mid x. In questo caso infatti si ha che:
In questi passaggi si può notare come la funzione di downcast s_i e la funzione \mathrm{t\_spazio}_{(n_i)} si semplifichino a vicenda: ciò è segno che l’approccio del downcast in questo caso non era necessario, ma il problema si poteva risolvere in modo più diretto. Questo è un problema dovuto al fatto che abbiamo ricavato la formula esatta partendo da una approssimata, in modo non proprio “pulito”. Se si possa fare di meglio, è ancora un punto aperto (v. fine dell’articolo).
Nella forma esplicita è più evidente la complessità della formula per il calcolo di \mathrm{t\_spazio} di secondo ordine. Questa complessità è anche dovuta alla presenza di tre operazioni di parte intera annidate:
- quella più esterna proviene dalla funzione di primo ordine \mathrm{t\_spazio}_{(n_i)}
- quella centrale proviene dalla funzione di downcast approssimata s^{\prime}_i
- quella più interna è necessaria per trasformare la funzione di downcast approssimata in una funzione di downcast esatta
Verifichiamo, mediante calcoli espliciti, che \mathrm{t\_spazio}_{(3, 5)}(10) = 17 (come visibile in Figura 3, aprendo i dettagli).
Innanzitutto S(T) = 8 non divide 10, quindi dobbiamo applicare il secondo caso della formula. Scegliamo la formula con i = 1:
I più curiosi potranno verificare che si perviene allo stesso risultato, con calcoli diversi, utilizzando la formula con i = 2.
Si potrebbe pensare che il Teorema T.13 (seconda forma) risolva definitivamente il problema della funzione \mathrm{t\_spazio} lineare di secondo ordine. Beh, un’espressione algebrica della funzione l’abbiamo trovata, ma secondo noi non è ancora abbastanza. In particolare, nutriamo forti dubbi sulla scalabilità della formula agli ordini superiori al secondo. Infatti, la formula per \mathrm{t\_spazio} è stata ottenuta da quella di \mathrm{t\_spazio}^{\prime} mediante un artificio tecnico, ma non è detto che si riesca a fare la stessa cosa per gli ordini superiori al secondo, dove le cose si complicano notevolmente. D’altra parte, se per gli ordini superiori ci limitassimo ad usare la formula di \mathrm{t\_spazio}^{\prime}, non è detto che questa sia sufficientemente precisa per essere utilizzata nelle dimostrazioni: infatti, se nel secondo ordine salta solo uno spazio per ogni periodo, la frazione di spazi saltati, sul numero di spazi totali del periodo, potrebbe crescere al crescere dell’ordine.
Quindi per noi la questione di \mathrm{t\_spazio} è ancora aperta, anche per il secondo ordine. Infatti la formula che calcola \mathrm{t\_spazio} di secondo ordine ha almeno tre difetti che ne rendono l’impiego poco agevole:
- è complicata
- è definita per casi
- contiene ben tre operazioni di parte intera, mentre la formula del primo ordine ne contiene una sola
Ci chiediamo quindi: è davvero necessaria una formula così complicata, definita per casi, e con tre parti intere, per calcolare la funzione \mathrm{t\_spazio} di secondo ordine? Oppure esiste una formula più semplice per calcolare la stessa funzione, magari non definita per casi e con meno di tre parti intere? Eventualmente, è possibile calcolare \mathrm{t\_spazio} di secondo ordine rinunciando all’approccio del downcast, ossia senza far ricorso alla funzione \mathrm{t\_spazio} di primo ordine? Per ora queste domande restano ancora senza risposta.