Prerequisito: Da un problema sulla corsa ai tratteggi
Nell’articolo precedente abbiamo visto che uno dei problemi fondamentali della teoria dei tratteggi è il calcolo delle funzioni \mathrm{t}, \mathrm{t\_valore} e \mathrm{t\_spazio}. Ora vediamo come si effettua questo calcolo per tratteggi lineari di primo ordine, mentre i prossimi articoli saranno dedicati ai tratteggi di ordine più alto. Consideriamo i tratteggi lineari perché, oltre ad essere abbastanza semplici, sono anche i puù importanti, essendo direttamente connessi coi numeri primi (si veda ad esempio Tratteggi e numeri primi).
Funzioni \mathrm{t} e \mathrm{t\_valore} lineari di primo ordine
Le formule per il calcolo delle funzioni \mathrm{t} e \mathrm{t\_valore} lineari di primo ordine (cioè \mathrm{t}_T e \mathrm{t\_valore}_T, con T lineare di primo ordine) derivano direttamente dalle principali definizioni della teoria dei tratteggi. Vediamo come.
Innanzitutto un tratteggio T di primo ordine ha una sola riga, che possiamo supporre abbia indice 1. Allora, essendo un tratteggio lineare, sappiamo che è una funzione del tipo
dove abbiamo chiamato n_1 l’unica componente del tratteggio. Dall’espressione della funzione T è evidente che i valori dei trattini sono tutti e soli i multipli non negativi di n_1.
Ad esempio, per n_1 = 3 abbiamo il seguente tratteggio, del quale visualizziamo sia i trattini in forma matematica, sia i loro ordinali, per x \gt 0:
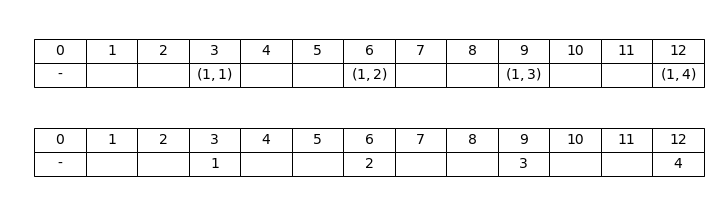
Come è evidente nell’esempio, in generale l’x-esimo trattino è (1, x) ed ha valore n_1 \cdot x. In generale, assumendo un indice generico al posto di 1, vale la seguente Proposizione:
Funzioni \mathrm{t} e \mathrm{t\_valore} lineari di primo ordine
Sia T = (n_i) un tratteggio lineare di primo ordine. Allora:
Poiché T ha solo una riga di indice i, tutti i suoi trattini sono del tipo (i, x). Applicando l’ordinamento (Definizione T.4 (Ordinamento dei trattini)) su questi trattini per x \gt 0, si trova che (1, 1) \lt (1, 2) \lt (1, 3) \lt \ldots. Allora l’x-esimo trattino, cioè \mathrm{t}_T(x) per la Definizione T.7 (Funzione \mathrm{t}), è (i, x).
Per quanto riguarda \mathrm{t\_valore}_T(x), per la Definizione T.8 (Funzione \mathrm{t\_valore}) si ha che \mathrm{t\_valore}_T(x) = T(\mathrm{t}_T(x)). Questo a sua volta, sostituendo la formula per la funzione \mathrm{t} appena ricavata, è uguale a T(i, x) = n_i \cdot x.
Conteggio dei trattini fino a un certo valore
Una proprietà semplice ma fondamentale per i tratteggi lineari di primo ordine è il conteggio dei trattini di valore minore o uguale ad un certo numero naturale v (escluso il trattino di valore 0, dato che le formule assumono una forma più semplice se non lo si considera). Per contare questi trattini possiamo contare i loro valori, ossia, assumendo i=1, i multipli positivi di n_1 minori o uguali a v. Infatti in un tratteggio di primo ordine non possono esserci due trattini con lo stesso valore (formalmente, esiste la corrispondenza biunivoca n_1 \cdot x \leftrightarrow (1, x) tra i trattini ed i loro valori), perciò ogni valore individua univocamente un trattino. Ad esempio, in Figura 1 i valori 3 e 6 individuano univocamente i trattini (1, 1) e (1, 2) rispettivamente, per cui il numero di trattini aventi valore positivo fino a 6 (due trattini) è pari al numero di multipli positivi di 3 minori o uguali a 6.
Si può dimostrare che il numero di multipli positivi di n_1 minori o uguali a v a sua volta è dato dalla parte intera di v diviso n_1, per cui in generale possiamo enunciare la seguente Proposizione:
Conteggio dei trattini fino a un certo valore in un tratteggio lineare di primo ordine
Sia T = (n_i) un tratteggio lineare di primo ordine. Il numero di trattini di T aventi valore positivo minore o uguale ad un certo numero naturale v è dato da:
Proviamo a dare una spiegazione intuitiva del motivo per cui il numero dei multipli di n_i minori o uguali a v è proprio \left \lfloor \frac{v}{n_i} \right \rfloor:
- Se v è multiplo di n_i, il numero di multipli di n_i minori o uguali a v è \frac{v}{n_i} = \left \lfloor \frac{v}{n_i} \right \rfloor. Ad esempio 2 = \frac{6}{3} = \left \lfloor \frac{6}{3} \right \rfloor è il numero di multipli di 3 minori o uguali a 6.
- Se invece v non è multiplo di n_i, il numero che cerchiamo è lo stesso che otterremmo se decrementassimo v di un’unità alla volta, fino ad arrivare ad un multiplo di n_1. Ad esempio, 8 e 7 non sono multipli di 3, mentre 6 lo è, perciò ricercare i multipli di 3 minori o uguali a 8, a 7 o a 6 è la stessa cosa. Quindi una formula che calcola il numero di multipli di n_i minori o uguali a x, se la chiamiamo f(x), deve essere tale f(8) = f(7) = f(6). Ma questo è proprio il comportamento della funzione f(x) = \left \lfloor \frac{x}{3} \right \rfloor, infatti \left \lfloor \frac{8}{3} \right \rfloor = \left \lfloor \frac{7}{3} \right \rfloor = \left \lfloor \frac{6}{3} \right \rfloor = \frac{6}{3} = 2.
È importante osservare che i trattini di valore minore di v sono quelli di valore minore o uguale a v - 1, ottenibili sempre con la Proposizione precedente. Perciò vale il seguente Corollario:
Conteggio dei trattini con valore minore di un certo numero in un tratteggio lineare di primo ordine
Sia T = (n_i) un tratteggio lineare di primo ordine. Il numero di trattini di T aventi valore positivo minore di un certo numero naturale v è dato da:
Funzione \mathrm{t\_spazio} lineare di primo ordine
Il calcolo della funzione \mathrm{t\_spazio} per un tratteggio lineare di primo ordine non è immediato come per \mathrm{t} e \mathrm{t\_valore}, ma ci si può arrivare partendo da un semplice ragionamento.
Supponiamo di avere un tratteggio lineare di primo ordine T = (n_1) e poniamo s := \mathrm{t\_spazio}_T(x). Ciò significa che:
- Tra le prime s colonne positive di T ci sono x spazi, l’ultimo dei quali è proprio s.
- Le s - x colonne che non sono spazi devono contenere per definizione almeno un trattino, ma essendo il tratteggio di primo ordine ne contengono uno solo.
I trattini individuati nel secondo punto sono tutti quelli aventi valore positivo minore o uguale ad s, o anche, dato che s è uno spazio, quelli di valore positivo minore di s. Allora il loro numero, se da una parte per costruzione è s - x, d’altra parte, per la Proposizione T.2 ed il suo Corollario, è dato rispettivamente dalle formule \left \lfloor \frac{s}{n_1} \right \rfloor e \left \lfloor \frac{s - 1}{n_1} \right \rfloor. Possiamo quindi scrivere l’equazione
Si può dimostrare che un intero s soddisfa l’equazione (1) se e solo se s = \mathrm{t\_spazio}_T(x) (finora abbiamo dimostrato solo che se s = \mathrm{t\_spazio}_T(x), allora s soddisfa la (1), non il viceversa). I dettagli di questa dimostrazione si trovano in Teoria dei tratteggi, Proposizione 8.1 pagg. 200-202.
Si può anche dimostrare che la (1) è equivalente alla singola equazione s - x = \left \lfloor \frac{s}{n_1} \right \rfloor, unita però alla condizione che s sia uno spazio. Infatti, il fatto che s è uno spazio equivale alla condizione \left \lfloor \frac{s}{n_1} \right \rfloor = \left \lfloor \frac{s - 1}{n_1} \right \rfloor, come asserito dalla seguente Proposizione:
Caratterizzazione degli spazi di un tratteggio lineare di primo ordine mediante un’equazione con la parte intera
Sia T = (n_1) un tratteggio lineare di primo ordine. Per ogni numero naturale s vale la seguente equivalenza:
Proponiamo due dimostrazioni: una più intuitiva ed una più tecnica. La prima è molto più semplice, ma è istruttivo conoscerle entrambe, per capire come a volte, se si guardano le cose dalla giusta propspettiva, si possono risparmiare molti calcoli.
Dimostrazione più intuitiva
Se s è uno spazio di T, non è il valore di un trattino, quindi il numero di trattini di valore minore o uguale ad s è pari al numero di trattini il cui valore è minore di s. Questo, per la Proposizione T.2 ed il suo Corollario, si traduce immediatamente nella condizione \left \lfloor \frac{s}{n_1} \right \rfloor = \left \lfloor \frac{s - 1}{n_1} \right \rfloor.
Viceversa, se \left \lfloor \frac{s}{n_1} \right \rfloor = \left \lfloor \frac{s - 1}{n_1} \right \rfloor, per la Proposizione ed il Corollario citati, significa che i trattini aventi valore minore di s sono tanti quanti quelli aventi valore minore o uguale ad s. Allora s non può essere il valore di un trattino, perchè, se così fosse, i due conteggi non coinciderebbero (i trattini con valore minore o uguale ad s sarebbero uno in più di quelli con valore minore). Quindi s deve essere uno spazio.
Dimostrazione più tecnica
Per dimostrare la Proposizione si può ricorrere alla Proprietà 2.21 a pag. 65 di Teoria dei tratteggi. Ponendo, nell’enunciato di questa Proprietà, nel caso particolare di k := 1, a := s - 1 e b := n_1, si ha che:
Ma nell’espressione a destra del segno di equivalenza, nell’enunciato da dimostrare, diciamo che \left \lfloor \frac{s}{n_1} \right \rfloor = \left \lfloor \frac{s - 1}{n_1} \right \rfloor: questo, alla luce della (2), significa che ((s - 1) \mathrm{\ mod\ } n_1 = n_1 - 1) = 0, ossia la condizione (s - 1) \mathrm{\ mod\ } n_1 = n_1 - 1 è falsa, cioè (s - 1) \mathrm{\ mod\ } n_1 \neq n_1 - 1:
Ora, per stabilire se s è uno spazio di T, dobbiamo capire quanto vale s \mathrm{\ mod\ } n_1. Applicando la Proprietà 2.4 a pag. 53 dell’op.cit., con a := s - 1, k = 1 ed n := n_1, si ottiene che:
Allora, nella (3), la condizione (s - 1) \mathrm{\ mod\ } n_1 \neq n_1 - 1 è equivalente alla condizione s \mathrm{\ mod\ } n_1 \neq 0, cioè al fatto che s è uno spazio di T. Per cui, ricapitolando:
Partendo dall’equazione (1), utilizzando la Proposizione T.5 e considerando un indice generico i al posto di 1, otteniamo l’equazione che chiameremo equazione caratteristica di \mathrm{t\_spazio} lineare di primo ordine:
Equazione caratteristica di \mathrm{t\_spazio} lineare di primo ordine
Sia T = (n_i) un tratteggio lineare di primo ordine. Allora
dove l’equazione a destra dell’equivalenza è detta equazione caratteristica di \mathrm{t\_spazio} lineare di primo ordine.
Consideriamo ancora il tratteggio (3) della Figura 1 e vediamo quali proprietà ha il suo settimo spazio, che risulta essere 10:
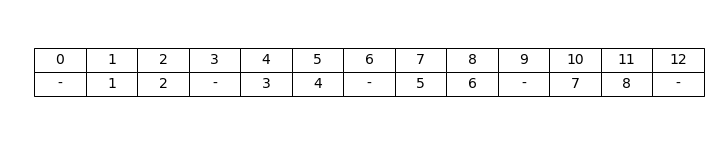
Vediamo che tra le prime 10 colonne positive del tratteggio vi sono:
- 7 spazi (1, 2, 4, 5, 7, 8, 10), l’ultimo dei quali è 10
- 3 colonne contenenti uno ed un solo trattino (3, 6, 9)
I tre trattini che abbiamo individuato sono quelli di valore positivo minore o uguale a 10, ma anche di valore minore di 10, dato che 10 è uno spazio. Allora per la Proposizione T.2 ed il suo Corollario, il loro numero è dato da \left \lfloor \frac{10}{3} \right \rfloor ed anche da \left \lfloor \frac{9}{3} \right \rfloor. In effetti, entrambe queste espressioni sono uguali a 3. Questo, per la
che, per la Proposizione citata, equivale a dire che 10 è uno spazio di T.
Più nello specifico, 10 è il settimo spazio di T, in quanto soddisfa l’equazione caratteristica con x = 7:
che per la Proposizione T.3 equivale a dire che 10 = \mathrm{t\_spazio}_T(7).
Per la Proposizione T.3, per calcolare la funzione \mathrm{t\_spazio} bisogna risolvere l’equazione caratteristica (4) nell’incognita s. La soluzione è data dal seguente Teorema, dimostrato in Teoria dei tratteggi, Teorema 8.1 pag. 202.
Formula per il calcolo di \mathrm{t\_spazio} lineare di primo ordine
Sia T = (n_i) un tratteggio lineare di primo ordine. Allora
Riprendendo l’esempio precedente, possiamo applicare la formula (5) con x = 7 ottenendo:
Ritroviamo così il risultato visibile in Figura 2.
Più in generale, applicando la formula (5) per x = 1, 2, 3, 4, 5, 6, 7, 8, \ldots otteniamo, facendo i conti, che \mathrm{t\_spazio}_{(3)}(x) = 1, 2, 4, 5, 7, 8, 10, 11, \ldots. Questo è un esempio del fatto che la formula (5) calcola nell’ordine tutti e soli gli spazi di un tratteggio lineare di primo ordine, saltando i multipli della componente del tratteggio (in questo caso 3).
L’equazione caratteristica (4) è abbastanza inusuale, per la presenza della parte intera, rispetto a quanto si insegna nella matematica scolastica. In teoria dei tratteggi invece equazioni di questo tipo sono abbastanza comuni, ed un modo per risolverle è applicare alcune proprietà che sono oggetto, per chi volesse approfondire, del Capitolo 2 di Teoria dei tratteggi.
Nonostante ciò, è possibile abbozzare la soluzione semplicemente rimuovendo le parti intere e risolvendo l’equazione algebrica risultante. Ad esempio, se ci soffermiamo sulla prima parte dell’equazione caratteristica:
Rimuovendo le parti intere abbiamo:
La soluzione approssimata ottenuta è molto simile alla soluzione esatta \left \lfloor \frac{n_1 x - 1}{n_1 - 1} \right \rfloor. Il problema principale è capire in generale quanto la soluzione trovata con questo metodo sia vicina a quella esatta: vedremo nei prossimi articoli che questo aspetto è di fondamentale importanza.