The goal
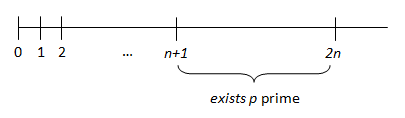
After the Theorem about the infinity of prime numbers, perhaps the simplest theorem which states something important about the distribution of prime numbers is the so called Bertrand’s Postulate.
Initially proposed as a conjecture in 1845 by the French mathematician Joseph Louis François Bertrand, the Postulate was later proved for the first time by the Russian Pafnutij L’vovič Chebyshev. It states that, for every integer number n \gt 0, there exists a prime number between n + 1 and 2n (ends included), as you can see alongside in the picture. So Bertrand’s Postulate establishes the existence of a prime number between 2 and 2, of one between 3 and 4, one between 4 and 6, one between 5 and 8, one between 6 and 10, and so on.
The path
We’ll not illustrate Chebyshev’s proof, which is rather complex, but the proof founded later by the Hungarian Paul Erdős (the same mathematician who, along with the Norwegian Atle Selberg, proved in an “elementary” way the Prime Number Theorem). This proof is interesting because it uses some combinatory techniques, based on the study of binomial coefficients.
From 1950 on, several stronger versions of the Postulate have been proved, but here we’ll propose the original version just because of its proof, that is an excellent example of the application of some elementary number theory techniques.
Map of paths for number theory
General introduction to paths