The proof of Goldbach’s Conjecture is one of the biggest still unsolved problems regarding prime numbers. Originally expressed by the mathematician Christian Goldbach, from whom the Conjecture takes its name, it was cited by Euler for the first time in 1742, in the form in which we know it today:
Every even number greater than 2 can be expressed as a sum of two prime numbers.
Besides this version of the Conjecture, another one exists, the so-called weak Goldbach’s Conjecture, which states that every odd number greater than 5 can be written as the sum of three primes (for example 7 = 2 + 2 + 3, 9 = 3 + 3 + 3, 11, = 3 + 3 + 5, …). It’s called “weak” Conjecture because, if Goldbach’s Conjecture (also known as “strong” Goldbach’s Conjecture, in order to distinguish it from the other one) was proved, the former would be a simple consequence.
On the other hand, while it’s true that Goldbach’s strong Conjecture implies the weak one, the converse is not true. In fact, the weak Conjecture has been proved by the Peruvian mathematician Harald Andrés Helfgott in 2013, but, nevertheless, the strong Conjecture continues to resist against all attempts to prove it.
But numbers look to speak for themselves…
The empirical evidence in favour of the conjecture is overwhelming: not only it looks that every even number greater than 2 can be expressed as a sum of two prime numbers, but, very often, different expressions of this kind exist for the same number. This can be seen even starting from the smallest numbers:
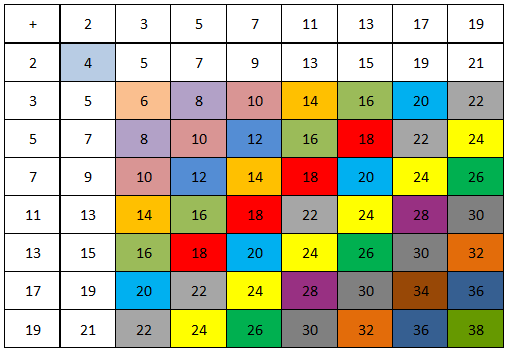
6 = 3 + 3
8 = 3 + 5
10 = 3 + 7 = 5 + 5
12 = 5 + 7
14 = 3 + 11 = 7 + 7
16 = 3 + 13 = 5 + 11
…
In particular, using our Goldbach pairs viewer, you can see that the number of different ways in which an even number can be expressed as a sum of two primes tends to grow as the considered number increases. This growth is shown in the following graph, the so-called Goldbach’s comet:
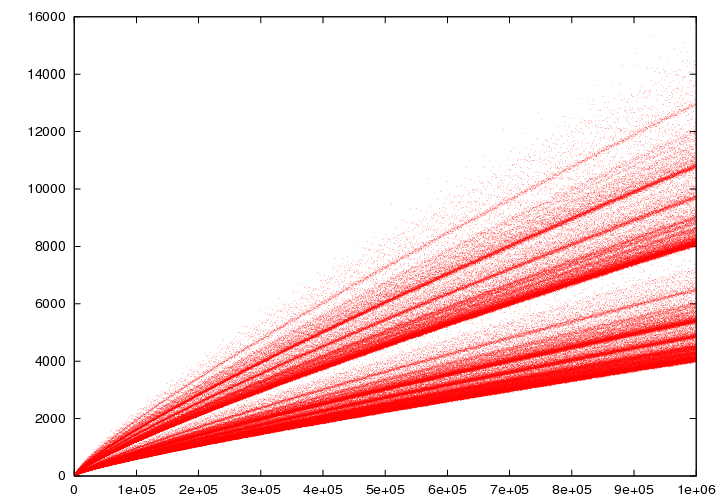
It’s not so easy as it looks
In spite of the empirical evidence and the simplicity of its statement, the Conjecture has been resisting to all proof attempts since almost three centuries. The hardest part to be faced in the proof is surely that the set of even numbers starting from 4 must be completely covered. That is, as the statement itself says, all even numbers greater than 2 must satisfy the relationship. Many proof attempts come to prove only that some even numbers satisfy it, for example the ones with some specific features or with a given algebraic form: as a result, the outcome of the proof isn’t the Conjecture, but something else.
For example, all even numbers of the form 2p, with p prime, are the sum of two primes (in this case, of p with itself), but, of course, not all even numbers respect this form. However, we can note that the set made of even numbers of type 2p is infinite, because primes are infinite, but this isn’t enough: just the fact that a set of even numbers is infinite does not imply that it contains all even numbers starting from 4. Even if we sum two odd prime numbers, we’ll always get an even number (because, generally, the sum of two odd numbers is even), in this case an even number greater or equal to 6, because the smallest sum of odd prime numbers is 6 = 3 + 3. So we’ll obtain an infinite set of even numbers greater or equal to 6, but just the fact that this set is infinite does not mean that it covers all even numbers starting from 6.
Ad additional aspect which you should consider, when you try to prove the Conjecture, is the difficulty of starting from arguments based on intuition and transform them into real proofs. For example, we know that:
- as n increases, the number of possible ways to write 2n as a sum of two positive integers, regardless of the order of the addends, is n, so it increases linearly;
- as a positive integer number x increases, by the Prime Number Theorem the number of primes less than or equal to x grows approximately like the function x / \log x.
These two aspects let us compute approximately, given a sum of the kind 2n = p + q, the number of the cases in which p is prime (regardless of wether q is prime or not). In particular, by the Prime Number Theorem the number of such cases increases as n increases. So the question becomes: among the cases in which p is prime, which increase with n, is there always one in which also q is prime?
This question is equivalent to ask wether the Conjecture is true or not. You may try to answer it affirmatively, starting from intuitive arguments. For example, the ratio between the number of cases in which at least p is prime and those ones in which both p and q are prime, as n increases, may become closer and closer to the the ratio between 2n and the number of prime numbers less than 2n, where the latter ratio in turn can be estimated by the previously cited Prime Number Theorem.
The problem of arguments of this kind is that they are often based on hypothesis, which seem plausible but are not proved (in this example, the hypothesis that the ratio is the same, which may not be true, though it may seem to be), so they are not valid proofs, even though they make use of mathematical formalisms and known theorems. Intuition can be a good guide in the proof of a theorem, but it must never be essential for the proof itself: a proof can contain intuitive arguments for better clarity, but not as an essential part of the argument, which instead must be rigorous.
As an example, we can cite Schinzel’s Hypothesis H_N:
Let f_1(t), f_2(t), \ldots, f_r(t) be irreducible polynomials with integer coefficients, and such that the coefficient of the maximum degree term is positive. Let g(t) be a polynomial with integer coefficients. Suppose that there are infinitely many positive integers N such that N - g(t) is irreducible, and that there is no prime number p such that, for every t, p is divisor of the value of the product f_1(t), \ldots, f_r(t) \cdot (N - g(t)). If N is large enough, then there exists an integer n such that N - g (n) is prime, and f_i(n ) is prime for all i = 1, \ldots, r.
By imposing the condition that N is even, setting r = 1 and f_1 (t) = g (t) = t, we’ll obtain this statement:
Let t be an irreducible polynomial with integer coefficients, and such that the coefficient of the term of greatest degree is positive. Let t be a polynomial with integer coefficients. Suppose there are infinitely many positive even integers N such that N - t is irreducible, and that there is no prime number p such that, for any t, p is divisor of the value of the product t \cdot (N - t). If N is large enough, then N - t is prime, and t is prime.
This statement can in turn be simplified, because:
- The polynomial t has coefficient 1 and its degree is 1, therefore the first two statements about t are obviously true;
- The degree of N - t is 1, so it is certainly irreducible;
- The fact that there is no prime number p such that, for every t, p is a divisor of the value of the product t \cdot (N - t) can be proved easily, for example by contradiction.
Therefore, by eliminating the related statements, we’ll obtain:
Any large enough even number is the sum of two prime numbers.
The final result is therefore a statement which is almost identical to Goldbach’s Conjecture, different from it only for the precondition that the starting even number is large enough. Despite this difference, this statement would still be a good starting point, because it would only remain to prove that the relationship is also valid beyond that precondition, that is for a finite number of cases.
Intermediate results
Several mathematicians proved some theorems which are weaker versions of the Conjecture. They can be grouped into two categories, according to what aspect of their statement differs from the Conjecture:
- The theorems that, instead of considering the sum of two primes (like in Goldbach’s Conjecture), consider a greater number of primes, or the sum of a prime and a semiprime, that is the product of two primes.
- The ones that, instead of being true for every even number greater than 2 (like in Goldbach’s Conjecture), are true for “almost” even numbers greater than 2.
Some theorems can be classified into both categories, as they state that “almost” all even numbers greater than two can be expressed as a somehow more complex sum than one involving two primes.
Regarding the correlation between even numbers and prime number pairs, some theorems from number theory can help stating something specific. For example, by using Dirichlet’s Theorem, we can state that infinite even numbers exist having 2 as the last digit, which are given by the sum of two primes.
The proof steps are the following:
- The last digit of the sum is 2, so the two addends can only have, as their last digit, respectively (0, 2), (1, 1), (2, 0), (3, 9), (4, 8), (5, 7), (6, 6), (7, 5), (8, 4), (9, 3); due to commutative property, we can just consider (0, 2), (1, 1), (3, 9), (4, 8), (5, 7), (6, 6).
- Dirichlet’s Theorem states that there exist infinite prime numbers of the type ax + b, with a and b coprime integers, and x integer. Then, for a = 10 and 0 \leq b \leq 9, there exist infinite prime numbers of the type 10x + b, i.e. with b as their last digit. But, in order to be able to apply the Theorem, b must be coprime with 10, so it must be equal to 1, 3, 7 or 9.
- In order to be able to apply Dirichlet’s Theorem to both addends (even if, actually, applying it to only one of them would be sufficient), we exclude from the previous possibilities the ones in which one of the two digits is not coprime with 10: the remaining possibilities are (1, 1) and (3, 9).
- Considering the case (1, 1), due to Dirichlet’s Theorem, the set P_1 := \{\text{primes having 1 as last digit}\} is infinite. Then, by summing two primes p, q \in P_1, since there are infinite possibilities for both of them, there are infinite possibilities for the sum, which will be an even number with 2 as its last digit.
- Considering instead the case (3, 9), due to Dirichlet’s Theorem, the sets P_3 := \{\text{primes having 3 as last digit}\} and P_9 := \{\text{primes having 9 as last digit}\} are infinite. Then, by summing a prime p \in P_1 with a prime q \in P_9, since there are infinite possibilities for both of them, there are infinite possibilities for the sum, which will be again an even number with 2 as its last digit.
The fact that several weaker versions of the Conjecture have been proved, without ever arriving to prove the original statement, makes us think that behind the Goldbach’s Conjecture there may be some deep mechanism that has yet to be understood, and which could require new proof techniques. For this reason we are sketching out the proof on the basis of a new theory, specifically built for studying the problem stated by the Conjecture: dashed line theory.
I would like experts to expose the errors in my simple proof, “The Stepladder Proof of the Goldbach Conjecture.” I posted it on Academia.edu.
In short, prime,prime pairs = total pairs – prime,composite pairs – composite,composite pairs.
Subject to known adjustments, every even number, n, can be expressed as n/4 unique and mandatory even number pairs. Each pair sum = n. Primes are embedded. (prime + 1) + (prime + 1) = n. For example, 200 has 50 unique and mandatory even number pairs. My excess pairs algorithm isolates 37 pairs with at least one composite. Prime,prime pairs = 50 – 37 = 13 exactly. The power and simplicity is in n/4.
Also email to [the email address has been omitted for avoiding spam]
Thanks for questions and comments.
Gregory Mazur
Dear Gregory, thanks for your comment. We are reading your proof and we’ll let you know by email. In the meantime, you may be interested in our proof strategies.
goldbach sanısının tek ispat yöntemi ortalama asal çift sayısını bulmak ile mümkündür. bu ortalama asal çiftleri bulmak için kullanılan formülde eğer asal çiftler gittikçe sıfıra yaklaşıyorsa sonuçta mutlaka asal çift oluşturmayan bir çift sayı vardır diyebiliriz eğer her olasılıkta bu formülümüz doğruya yakın bir değer veriyor ve formül sonucu asla sıfıra yaklaşmıyorsa her çift sayı için mutlaka bir en az birtane asal çift vardır deriz
Collatz sanısı çözüldü. çözümü anlamak ve sonsuzluktaki resmi çekmek için collatz sayıları’nın “Çözümsüzlükteki düzen” yazısı’nı mutlaka okuyun yazısı linkte
drive.google.com/file/d/1bS1OvEdDVgDMDxk70k5DyFqLG4ILc1xt/view?usp=sharing
Aşağıdaki tüm problemler çözüldü ispatlandı.
collatz sanısı çözümsüz olarak ispatlandı.
drive.google.com/file/d/1WHBTgbyVOOGJ-5ggCZxCXdnEs9FmPyFK/view
goldbach sanısı ispatlandı
basit matematik ile goldbach sanısı ispatlandı açıklama dosyası linkte
1drv.ms/w/s!AlSwXcQnq6P1iDtf7zTF8wZL1_1_
youtube video link
kzclip.com/channel/UC3qewBWD7TjLf7RENRZXj5A
ikiz asal sayılar ispatlandı
aralarındaki fark 2n olan tüm ikiz asal sayılar ispatlandı aralarındaki fark 2 olan ikiz asal sayılar cetveli var
docs.google.com/spreadsheets/d/1-cdTvu-U7SeAmQ3thGPMds3yIQJrRRLAQYurqVZTU6k/edit?ts=5bd8b619#gid=1327248543
İrfan Aydoğan
doktor0906@hotmail.com
doktorg0906@gmail.com
Please note: we exceptionally accepted this comment written in Turkish, because the author explained to us that he doesn’t know English enough. We think that language should not be a barrier for research, so we decided to publish this comment. We published it exactly as it was written, for our readers who know Turkish. For the other readers, here is an English translation adapted from the one given by Google translate:
The only proof method of Goldbach’s conjecture is to find the average number of prime pairs. In the formula used to find these average prime pairs, if the prime pairs are getting closer and closer to zero, we can say that there is an even number that does not necessarily form a prime pair.
Collatz conjecture has been resolved. To understand the solution and take the picture to infinity, be sure to read the “Order in no solution” article about the Collatz numbers at the link below.
drive.google.com/file/d/1bS1OvEdDVgDMDxk70k5DyFqLG4ILc1xt/view?usp=sharing
All the following problems have been solved.
Collatz conjecture proved unsolved.
drive.google.com/file/d/1WHBTgbyVOOGJ-5ggCZxCXdnEs9FmPyFK/view
Goldbach’s conjecture proved
With simple math, Goldbach’s conjecture is proved.
1drv.ms/w/s!AlSwXcQnq6P1iDtf7zTF8wZL1_1_
youtube video link
kzclip.com/channel/UC3qewBWD7TjLf7RENRZXj5A
twin prime numbers proved
There is a ruler of twin prime numbers the difference of which is 2
docs.google.com/spreadsheets/d/1-cdTvu-U7SeAmQ3thGPMds3yIQJrRRLAQYurqVZTU6k/edit?ts=5bd8b619#gid=1327248543
İrfan Aydoğan
doktor0906@hotmail.com
doktorg0906@gmail.com