La dimostrazione della Congettura di Goldbach è uno dei più grandi problemi ancora irrisolti che riguardano i numeri primi. Inizialmente formulata dal matematico Christian Goldbach, dal quale prende il nome, è stata citata da Eulero per la prima volta nel 1742, nella forma in cui la conosciamo oggi:
Ogni numero pari maggiore di 2 può essere scritto come somma di due numeri primi.
Oltre a questa versione della Congettura, ne esiste una seconda, la cosiddetta Congettura debole di Goldbach, che afferma che ogni numero dispari maggiore di 5 può essere scritto come somma di tre numeri primi (ad esempio 7 = 2 + 2 + 3, 9 = 3 + 3 + 3, 11, = 3 + 3 + 5, …). Essa è chiamata Congettura “debole” perché, se si dimostrasse la Congettura di Goldbach (nota anche come Congettura “forte” di Goldbach, per distinguerla dall’altra), essa ne sarebbe una semplice conseguenza.
D’altra parte, se è vero che la Congettura forte di Goldbach implica quella debole, non è vero il viceversa. Infatti, la Congettura debole è stata dimostrata dal matematico peruviano Harald Andrés Helfgott nel 2013, ma, ciononostante, la Congettura forte continua a resistere a tutti i tentativi di dimostrazione.
Eppure i numeri sembrano parlare chiaro…
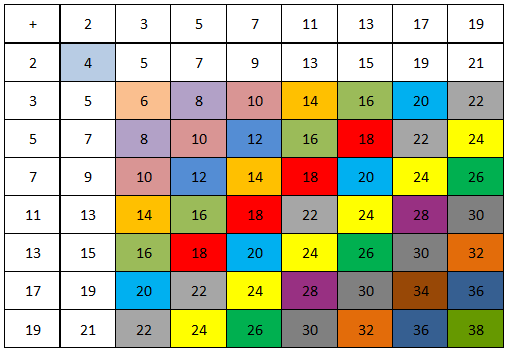
L’evidenza empirica a favore della Congettura è schiacciante: non solo sembra che ogni numero pari maggiore di 2 possa essere scritto come somma di due numeri primi, ma molto spesso esistono diverse scritture di questo tipo per lo stesso numero. Ciò è evidente anche partendo dai numeri più piccoli:
6 = 3 + 3
8 = 3 + 5
10 = 3 + 7 = 5 + 5
12 = 5 + 7
14 = 3 + 11 = 7 + 7
16 = 3 + 13 = 5 + 11
…
In particolare, utilizzando il nostro visualizzatore di coppie di Goldbach, è possibile verificare che il numero di modi diversi in cui un numero pari può essere scritto come somma di due numeri primi tende ad aumentare al crescere del numero considerato. Questa crescita è visibile nel grafico seguente, la cosiddetta “cometa di Goldbach”:
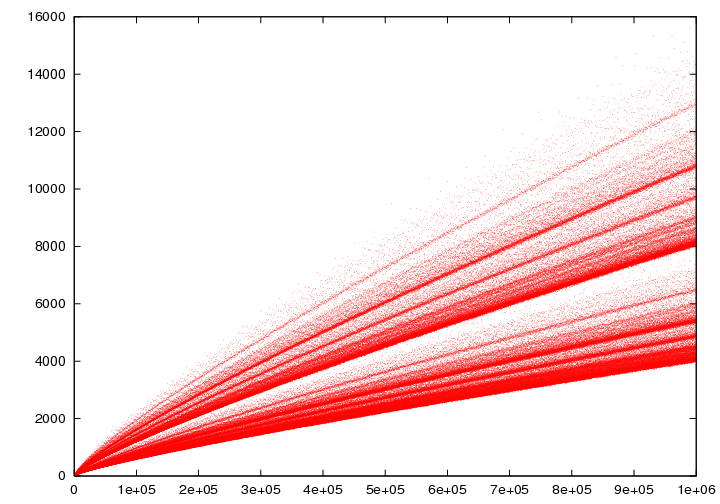
Non è facile come sembra
Nonostante l’evidenza empirica e la semplicità dell’enunciato, la Congettura resiste a tutti i tentativi di dimostrazione da quasi tre secoli. La parte più difficile da affrontare nella dimostrazione è sicuramente il fatto che l’insieme dei numeri pari da 4 in poi dev’essere completamente coperto, ossia, come dice l’enunciato stesso, tutti i numeri pari maggiori di 2 devono soddisfare la relazione. Molti tentativi di dimostrazione della Congettura arrivano invece a dimostrare solo che alcuni numeri pari la soddisfano, ad esempio quelli che rispettano certe caratteristiche o hanno una certa forma algebrica: il risultato è che non viene dimostrata la Congettura, ma qualcos’altro.
Ad esempio, tutti i numeri pari della forma 2p, con p primo, sono la somma di due numeri primi (in questo caso di p con se stesso), ma certamente non tutti i numeri pari sono di questa forma. Eppure, si può osservare che l’insieme dei numeri pari del tipo 2p è infinito, perché i numeri primi sono infiniti, ma ciò non basta: il solo fatto che un insieme di numeri pari sia infinito non implica che esso contenga tutti i numeri pari da 4 in poi. Anche sommando tra loro due numeri primi dispari si ottiene sempre un numero pari (perché in generale la somma di due numeri dispari è pari), in questo caso da 6 in poi perché la più piccola somma di primi dispari è 6 = 3 + 3. Così si ottiene un insieme infinito di numeri pari maggiori o uguali a 6, ma il solo fatto che questo insieme sia infinito non significa che esso esaurisca tutti i numeri pari da 6 in poi.
Un ulteriore aspetto da considerare, quando si prova a dimostrare la Congettura, è la difficoltà di partire da argomentazioni basate sull’intuizione e trasformarle in dimostrazioni vere e proprie. Ad esempio, sappiamo che:
- al crescere di n, il numero di possibili scritture di 2n come somma di due numeri positivi, a meno dell’ordine degli addendi, è proprio n, quindi aumenta in modo lineare;
- al crescere di un numero intero positivo x, per il Teorema dei Numeri Primi il numero di primi minori o uguali ad x cresce più o meno come la funzione x / \log x.
Questi due aspetti permettono di calcolare, in una somma del tipo 2n = p + q, quanti sono all’incirca i casi in cui p è primo (senza tener conto se q è primo o no). In particolare, il Teorema dei Numeri Primi ha come conseguenza il fatto che il numero di questi casi aumenta al crescere di n. La domanda quindi diventa: tra i casi in cui p è primo, che crescono rispetto ad n, ce n’è sempre almeno uno in cui anche q è primo?
A quest’ultima domanda, che equivale a chiedersi se la Congettura è vera oppure no, si può tentare di rispondere affermativamente partendo da argomentazioni di tipo intuitivo. Per esempio, il rapporto tra il numero di casi in cui almeno p è primo e quelli in cui sia p che q sono primi potrebbe, al crescere di n, avvicinarsi al rapporto tra 2n e il numero di numeri primi minori di 2n, dove quest’ultimo rapporto a sua volta è stimabile mediante il Teorema di Numeri Primi citato in precedenza.
Il problema dei ragionamenti di questo tipo è che spesso si basano su ipotesi che sembrano plausibili ma non sono dimostrate (in questo esempio, che il rapporto sia lo stesso, il che non è detto che sia vero, anche se magari può sembrarlo), per cui non costituiscono delle dimostrazioni valide, pur utilizzando formalismi matematici e teoremi noti. L’intuizione può essere una buona guida nella dimostrazione di un teorema, ma non deve mai essere essenziale per la dimostrazione stessa: una dimostrazione può contenere discorsi intuitivi per una maggiore chiarezza, ma non come parte integrante del ragionamento, che invece deve essere rigoroso.
A titolo di esempio, si può citare l’Ipotesi H_N di Schinzel:
Siano f_1(t), f_2(t), \ldots , f_r(t) polinomi irriducibili con coefficienti interi, e tali che il coefficiente del termine di grado massimo sia positivo. Sia g(t) un polinomio con coefficienti interi. Supponiamo che esistano infiniti interi positivi N tali che N - g(t) sia irriducibile, e che non esista un numero primo p tale che, per ogni t, p è divisore del valore del prodotto f_1(t), \ldots , f_r(t) \cdot (N - g(t)). Se N è abbastanza grande, allora esiste un intero n tale che N - g(n) è primo, e f_i(n) è primo per tutti gli i=1, \ldots , r.
Imponendo la condizione che N sia pari, ponendo r = 1 e f_1(t) = g(t) = t, si ottiene questo enunciato:
Sia t un polinomio irriducibile con coefficienti interi, e tale che il coefficiente del termine di grado massimo sia positivo. Sia t un polinomio con coefficienti interi. Supponiamo che esistano infiniti interi positivi pari N tali che N - t sia irriducibile, e che non esista un numero primo p tale che, per ogni t, p è divisore del valore del prodotto t \cdot (N - t). Se N è abbastanza grande, allora N - t è primo, e t è primo.
Questo enunciato è a sua volta semplificabile, perché:
- Il polinomio t ha coefficiente 1 ed è di primo grado, quindi le prime due affermazioni relative a t sono ovviamente vere;
- N - t è di primo grado, quindi è sicuramente irriducibile;
- Il fatto che non esiste un numero primo p tale che, per ogni t, p è divisore del valore del prodotto t \cdot (N - t) si può dimostrare facilmente, ad esempio ragionando per assurdo.
Per cui, eliminando le relative affermazioni, si ottiene:
Ogni numero pari abbastanza grande è somma di due numeri primi.
Il risultato finale è quindi un enunciato quasi identico alla Congettura di Goldbach, differente da essa solo per la precondizione che il numero pari di partenza sia abbastanza grande. Nonostante questa differenza, si tratterebbe comunque di una buona base di partenza, dato che resterebbe solo da dimostrare che la relazione vale anche al di fuori di quella precondizione, ossia per un numero finito di casi.
Risultati intermedi
Diversi matematici hanno dimostrato alcuni teoremi che costituiscono delle versioni meno forti della Congettura. Questi teoremi possono essere classificati in due categorie, a seconda di quale aspetto dell’enunciato cambia rispetto alla Congettura:
- I teoremi che, invece che considerare la somma di due numeri primi (come nella Congettura di Goldbach), considerano quella di un numero più grande di numeri primi, oppure di un numero primo e di un numero semiprimo, cioè il prodotto di due numeri primi.
- Quelli che, invece che valere per ogni numero pari maggiore di 2 (come nella Congettura di Goldbach), valgono per “quasi” tutti i numeri pari maggiori di 2.
Alcuni teoremi rientrano in entrambe le categorie, affermando che “quasi” tutti i numeri pari maggiori di 2 possono essere scritti come una somma più complessa della somma di due numeri primi.
Relativamente alla correlazione tra numeri pari e coppie di numeri primi, alcuni teoremi di teoria dei numeri possono aiutare ad affermare qualcosa di abbastanza specifico. Ad esempio, tramite il Teorema di Dirichlet, è possibile dimostrare che esistono infiniti numeri pari aventi come ultima cifra 2 che sono dati dalla somma di due numeri primi.
I passaggi logici della dimostrazione sono i seguenti:
- Dato che l’ultima cifra della somma è 2, i due addendi possono solo avere come ultima cifra rispettivamente (0, 2), (1, 1), (2, 0), (3, 9), (4, 8), (5, 7), (6, 6), (7, 5), (8, 4), (9, 3); tenendo conto della proprietà commutativa, possiamo limitarci a considerare (0, 2), (1, 1), (3, 9), (4, 8), (5, 7), (6, 6).
- Il Teorema di Dirichlet dice che esistono infiniti numeri primi del tipo ax + b, con a e b interi coprimi, e x intero. Quindi, per a = 10 e 0 \leq b \leq 9, esistono infiniti numeri primi del tipo 10x + b, ossia con ultima cifra b. Ma, per poter applicare il Teorema, b deve essere coprimo con 10, ossia dev’essere uguale a 1, 3, 7 oppure 9.
- Per poter applicare il Teorema di Dirichlet a entrambi gli addendi (anche se in realtà basterebbe applicarlo a uno solo), escludiamo dalle possibilità precedenti quelle in cui una delle due cifre non è coprima con 10: restano (1, 1) e (3, 9).
- Considerando il caso (1, 1), per il Teorema di Dirichlet l’insieme P_1 := \{\text{numeri primi aventi come cifra finale 1}\} è infinito. Allora, sommando due numeri primi p, q \in P_1, essendoci infinite possibilità per entrambi, abbiamo infinite possibilità per la somma, che sarà un numero pari con cifra finale 2.
- Considerando invece il caso (3, 9), per il Teorema di Dirichlet gli insiemi P_3 := \{\text{numeri primi aventi come cifra finale 3}\} e P_9 := \{\text{numeri primi aventi come cifra finale 9}\} sono infiniti. Allora, sommando un primo p \in P_1 ed un primo q \in P_9, essendoci infinite possibilità per entrambi, avremo infinite possibilità per la somma, che sarà ancora un numero pari con cifra finale 2.
Il fatto che siano state dimostrate diverse versioni più deboli della Congettura, senza mai arrivare a dimostrare l’enunciato originale, ci fa pensare che dietro la Congettura di Goldbach ci possa essere qualche meccanismo profondo che deve essere ancora compreso, e che potrebbe richiedere nuove tecniche di dimostrazione. Per questo stiamo impostando la dimostrazione sulla base di una nuova teoria, costruita appositamente per studiare lo specifico problema posto dalla Congettura: la teoria dei tratteggi.