La Congettura di Goldbach si colloca nell’ambito della Teoria dei numeri, la branca della matematica che studia i numeri interi. Per comprendere le dimostrazioni dei risultati simili alla Congettura, e molto probabilmente anche per dimostrare la Congettura stessa, sono richieste solide conoscenze di teoria dei numeri. Queste conoscenze, però, raramente entrano a far parte del curriculum di studi di un matematico. Di fatto la teoria dei numeri è considerata un ambito molto specialistico su cui improntare, per esempio, degli esami universitari a scelta oppure, per i più appassionati, un dottorato di ricerca. Ma non è necessario arrivare a tanto per intraprendere uno studio serio della teoria dei numeri. Infatti, molte nozioni richiedono solamente una buona conoscenza della matematica scolastica e dell’analisi reale in una variabile, pertanto sono perfettamente alla portata di uno studente del primo anno di un corso di laurea scientifico.
Siamo partiti da queste considerazioni per ideare questa sezione del sito, con lo scopo di avvicinare alla teoria dei numeri il maggior numero possibile di persone. Abbiamo suddiviso il materiale in diversi percorsi tematici, ciascuno con un proprio obiettivo, che nella maggior parte dei casi consiste nella dimostrazione di un teorema specifico. Ogni percorso è composto da diversi articoli, presentati nell’ordine di lettura consigliato, in modo tale che ciascun articolo si trovi prima di altri eventuali articoli che vi fanno riferimento.
La fonte da cui siamo partiti è il testo An introduction to the theory of numbers di G. H. Hardy ed E. M. Write, uno dei classici della materia. Il materiale che presentiamo nei nostri articoli è una forte rielaborazione di alcune parti di questo testo: abbiamo introdotto degli esempi, alcuni lemmi e definizioni, abbiamo evidenziato le idee e le tecniche chiave, ed esplicitato molti dettagli che nel testo originale sono sottintesi.
Come riferimento interno a questa sezione del sito, abbiamo creato un elenco degli enunciati e un elenco delle definizioni e dei simboli utilizzati.
Visualizza la mappa dei percorsi
| Percorso | Numero di articoli |
|---|---|
| Fondamenti di teoria dei numeri
|
21 |
| Il Postulato di Bertrand
|
4 |
| Il Teorema di Chebyshev (versione debole)
|
7 |
| Il Teorema di Chebyshev (versione forte)
|
15 |
| Il Teorema dei Numeri Primi: la dimostrazione “elementare”
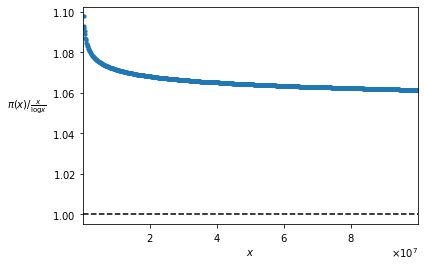
L’obiettivo di questo percorso è dimostrare uno dei più importanti teoremi che riguardano i numeri primi, il cosiddetto Teorema dei Numeri Primi, il cui enunciato può essere espresso con la formula seguente: \pi(x) \sim \frac{x}{\log x}
dove \pi(x) indica il numero di numeri primi minori o uguali ad x. Il simbolo \sim rappresenta un’uguaglianza asintotica, il cui significato è chiarito in uno dei nostri articoli. Tuttavia, semplificando, possiamo leggere la formula dicendo che ci sono all’incirca \frac{x}{\log x} numeri primi minori o uguali ad x, e questa stima diventa sempre più accurata al crescere di x. |
28 |
| Il Teorema di Chen
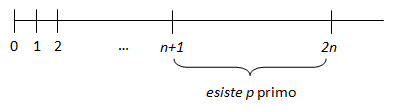
L’obiettivo di questo percorso è dimostrare uno dei teoremi più simili alla Congettura di Goldbach, il Teorema di Chen, il cui enunciato può essere espresso come segue: Ogni numero pari sufficientemente grande è somma o di due numeri primi, o di un primo e un semiprimo (ossia un prodotto di due numeri primi). Questo Teorema fu dimostrato per la prima volta dal matematico cinese Chen Jingrun nel 1966 (successivamente la dimostrazione fu perfezionata sia da lui stesso che da altri matematici). La dimostrazione si basa su una teoria matematica che prende il nome di teoria dei crivelli, sviluppatasi pochi anni prima ma dalle origini antichissime, che si possono far risalire al matematico dell’antica Grecia Eratostene di Cirene, inventore dell’omonimo crivello, il primo in assoluto. Chiaramente da allora la teoria dei crivelli si è evoluta parecchio, ma è rimasta sempre una teoria “elementare”, ossia non basata sull’analisi complessa. |
6 (incompleto) |
| Materiale complementare
|
3 |