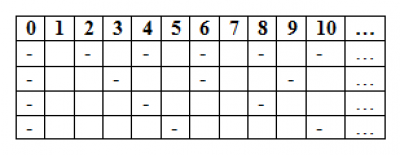
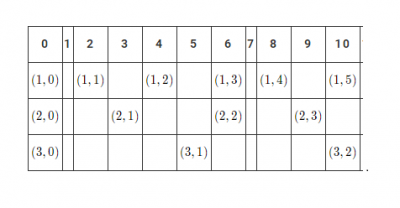
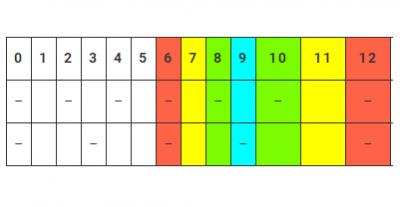
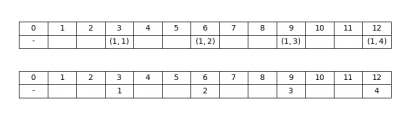
La teoria dei tratteggi è una nuova teoria matematica che studia il rapporto tra la successione dei numeri naturali e la loro relazione di divisibilità. Problemi tipici sono il calcolo dell'n-esimo numero naturale divisibile per almeno uno di k numeri fissati, o non divisibile per alcuno di essi. Per tale natura, la teoria si presta allo studio dei numeri primi mediante un approccio costruttivo, ispirato al crivello di Eratostene...
La nascita della teoria è avvenuta tra i banchi di scuola, con l'obiettivo di creare uno strumento utile per la dimostrazione della congettura di Goldbach.
Quando il professore di matematica di Simone, in terzo liceo, gli parlò della congettura di Goldbach, egli sentì l'irresistibile desiderio di capirla in maniera profonda, per tentate di dimostrarla. Alcuni compagni di classe seguirono i suoi primi ragionamenti, però il loro interesse non derivava tanto dal problema in sé, quanto dal premio di un milione di dollari che allora era in palio per chiunque fosse riuscito a dimostrarla. Anche per Simone il premio era importante, ma non come il desiderio di conoscere i meccanismi che si celano dietro il semplice enunciato della congettura. Cosí i suoi compagni si disinteressarono presto alla questione, mentre lui fu impegnato, negli anni successivi, a sviluppare una nuova teoria matematica che riteneva essere uno strumento utile per la dimostrazione. Chiamò questa teoria col nome di teoria dei tratteggi.
Ma perché ideare una teoria nuova, solamente per risolvere uno specifico problema? Egli pensò che, se nessuno era ancora riuscito a dimostrare la congettura, un motivo poteva essere la mancanza dei giusti strumenti matematici. Perciò valeva la pena provare con un approccio nuovo, basato su una nuova teoria.
Nel 2010 vi è stata la prima pubblicazione in una forma compiuta, sul sito http://teoriadeitratteggi.webnode.it, essa però utilizza un linguaggio molto formale, che lascia poco spazio all'intuizione. Questo aspetto è stato migliorato a partire dal 2018, con la nascita del progetto Dimostriamo Goldbach!, grazie al quale gli argomenti della teoria dei tratteggi sono stati spiegati con un taglio più didattico, con l'ausilio di immagini ed esempi, dando luogo agli articoli elencati sotto.
Sempre nell'ambito del progetto Dimostriamo Goldbach!, vi sono stati ulteriori sviluppi della teoria, più legati alla ricerca della dimostrazione della congettura di Goldbach. A breve li raccoglieremo un una nuova sezione di questo sito.
Come riferimento interno a questa sezione del sito, abbiamo creato un elenco delle definizioni e dei simboli utilizzati.