Lemoine’s Conjecture
The first of these conjectures, as sometimes happens in the scientific field, was born twice. The statement, as we currently know it, is the following:
Every odd number greater than 5 can be written as p + 2q, where p and q are odd primes, not necessarily distinct.
Some examples follow:
The first known formulation appeared in 1895, in the first issue of the scientific journal L’Intermédiaire des mathématiciens, in this form:
Theorem that I have found empirically and of which I ask, if possible, to prove its correctness or falsity. I have done a lot of checks.
Any odd number 2n + 1 (n > 1) is, (expressible) in many ways, (as) the sum of a prime number and the double of a prime number.
The author of this formulation is the French engineer and mathematician Émile Michel Hyacinthe Lemoine, who is also the founder of the magazine, together with his friend Charles-Ange Laisant, also a mathematician.
This conjecture did not have much visibility, until, in 1963, history repeated itself almost identically: the Scottish philosopher and mathematician Hyman Levy repeated the same conjecture in another journal, The Mathematical Gazette.

It wasn’t a quote, but neither a plagiarism, as Levy did not know about Lemoine’s work. His result, unlike the previous one, had a greater diffusion and aroused more interest, so, in the first publications that referred to it, the sentence was called Levy’s Conjecture, while today it is found also as Lemoine’s Conjecture, to give also credit to who discovered it first.
The “A” Conjecture by Hardy and Littlewood
At the beginning of the 20th century, the two British mathematicians Godfrey Harold Hardy and John Edensor Littlewood, both members of the prestigious Royal Society, undertook a series of joint studies on prime numbers, which lasted several years. Such was the fame of this association that, as the Danish mathematician Harald Bohr said at a lecture, in that period there were “only three really great English mathematicians: Hardy, Littlewood, and Hardy–Littlewood”.
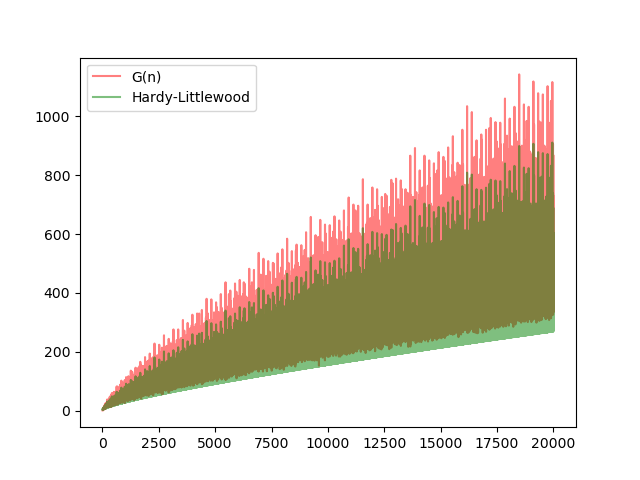
In their paper Some problems of Partitio numerorum; III: On the expression of a number as a sum of primes, published in 1923 on number 44 of the scientific journal Acta Mathematica, presented some of their hypotheses about the subject, each marked by a letter. One in particular, the Conjecture A, states that:
Every large enough even number is the sum of two odd prime numbers. The asymptotic formula for the number of representations is
where p is a prime odd divisor of n, and
where w is a prime number.
The constant C_2 is currently known as the twin primes constant, since it appears in many theorems related to twin primes.
It is evident that the first part of the statement presents analogies with Goldbach’s Strong Conjecture, but also with Chen’s Theorem.
The following chart shows a comparison between the actual number of sums of prime numbers, i.e. Goldbach pairs, and the value of expression (1) for even numbers from 6 to 20,000:
Dubner’s Conjecture
One of the many possible ways of proving Goldbach’s Conjecture is to try to find an even stronger version of it and prove that. This lead was followed by the American mathematician Harvey Dubner, who, in his article Twin Prime Conjectures of 1996, formulated the following conjecture, reported in the text as “Conjecture 4A”:
All even numbers greater than 4206 are the sum of two prime numbers that have a twin.
Here are two examples (both show only one sum, but there can be more than one):
5000 = 31 + 4969, where 31 has the twin 29, and 4969 has the twin 4967.
9936 = 4967 + 4969, where 4967 and 4969 are twins of each other.
If Dubner’s Conjecture were true, so would Goldbach’s Conjecture, given that:
- We already know that even numbers greater than 2 up to 4206 are the sum of two prime numbers;
- By Dubner’s Conjecture, even numbers greater than 4206 would be the sum of two prime numbers;
- So, in total, all even numbers greater than 2 would be the sum of two prime numbers.