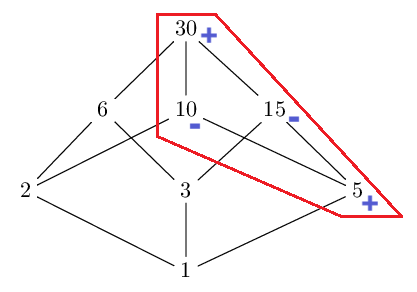
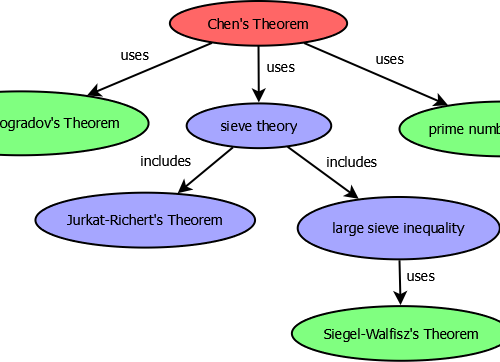
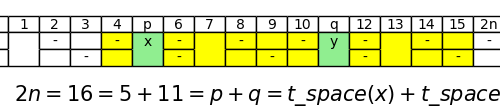
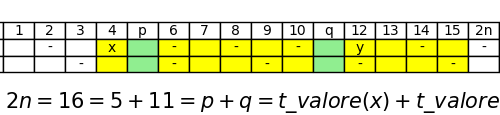
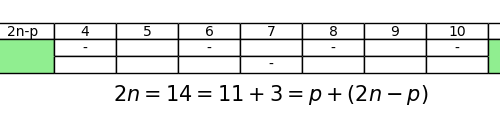
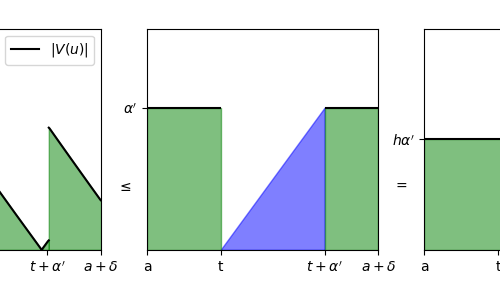
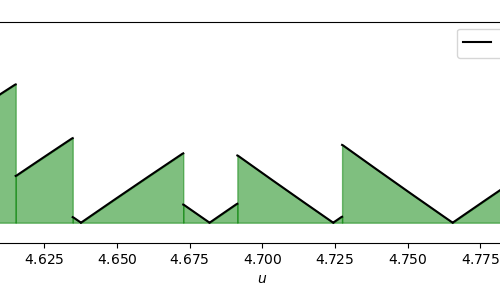
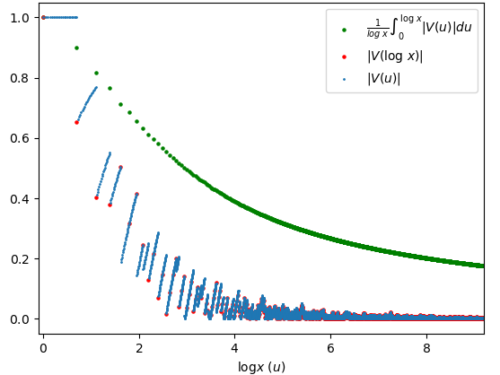
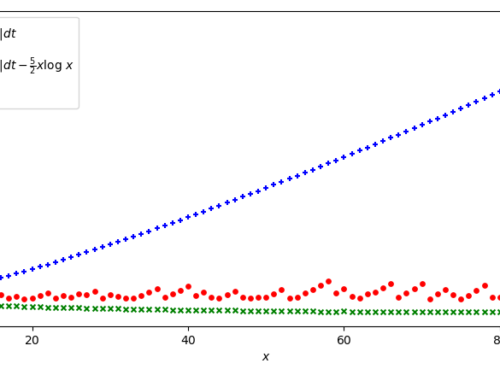
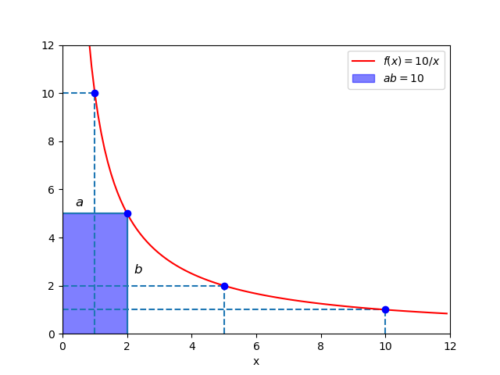
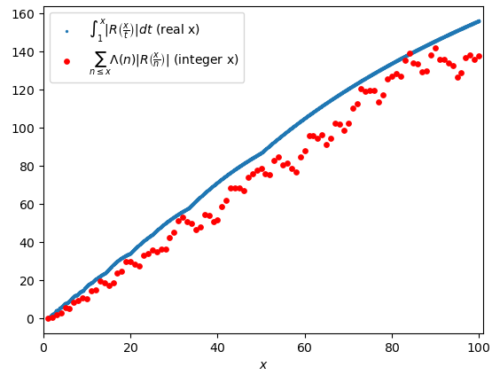
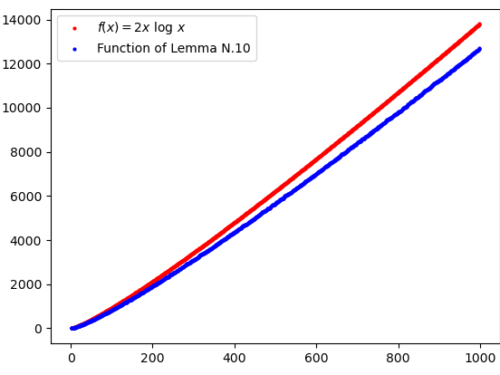
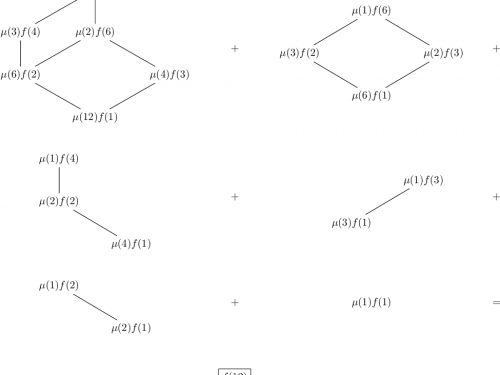
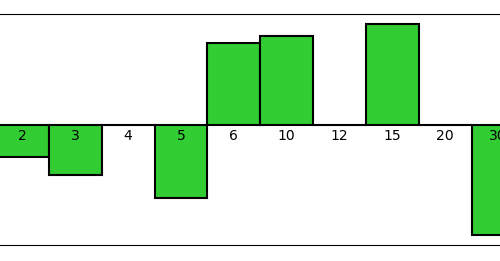
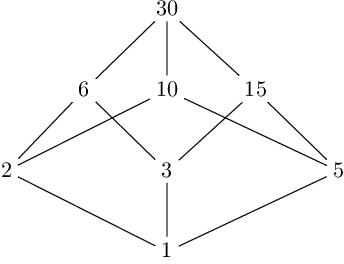
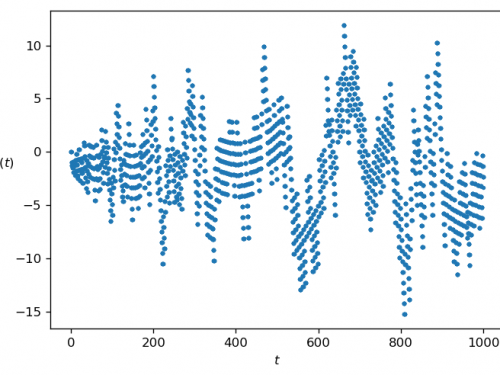
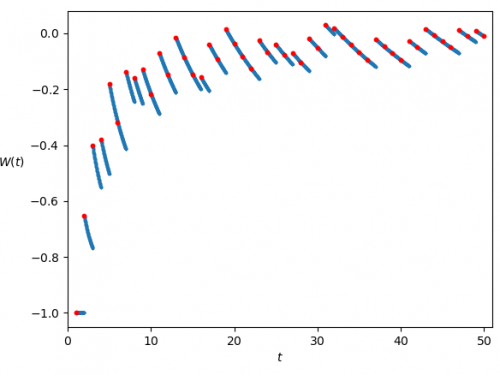
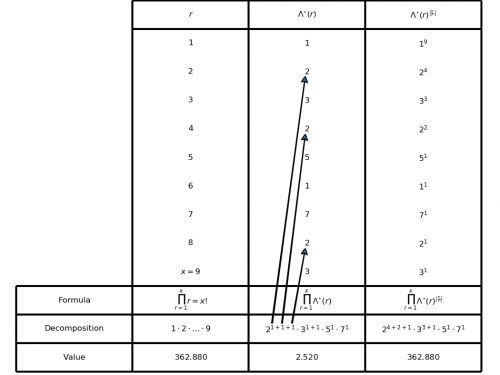
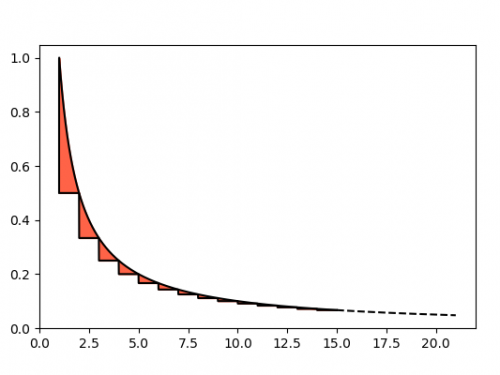
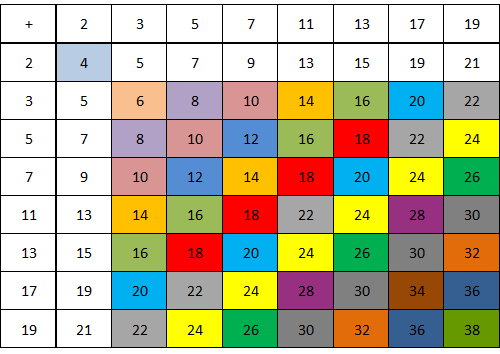
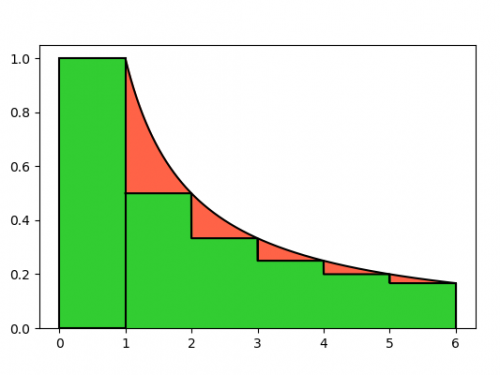
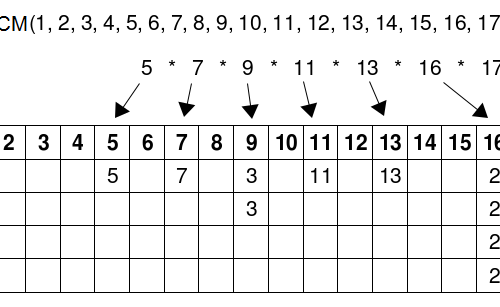
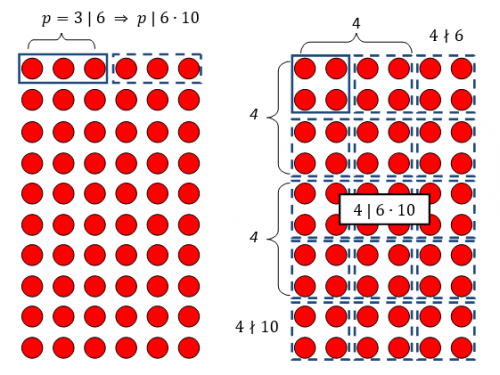
Selberg’s sieve: study of the parameters λ
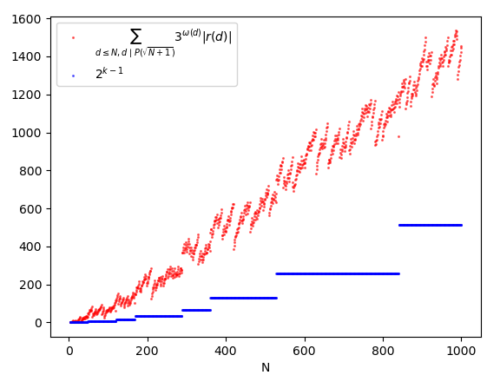
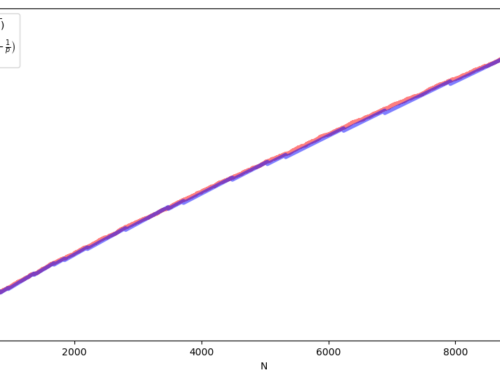
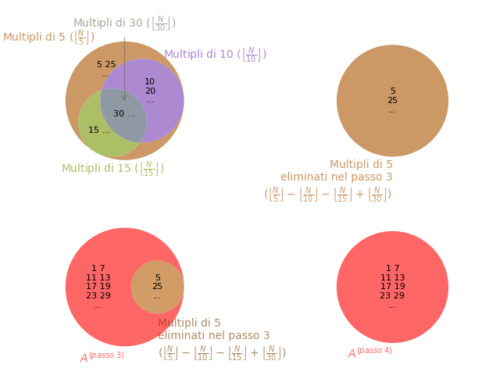
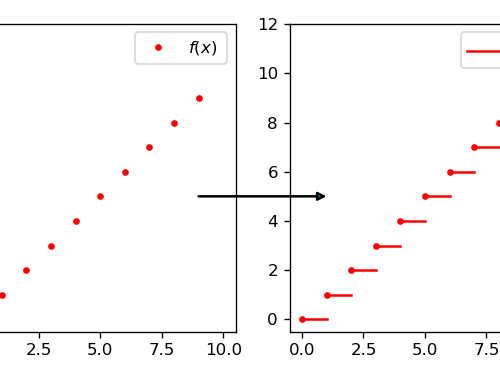
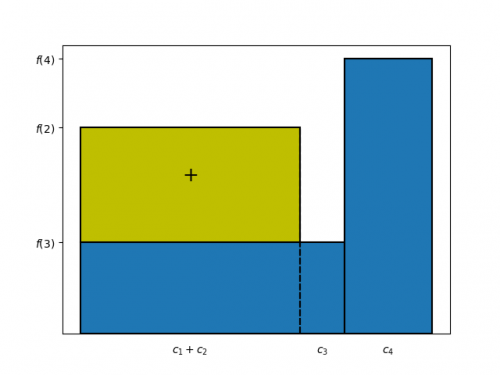
As we have seen, some parameters λd appear in the Selberg's sieve formula, which are used both in the estimation…
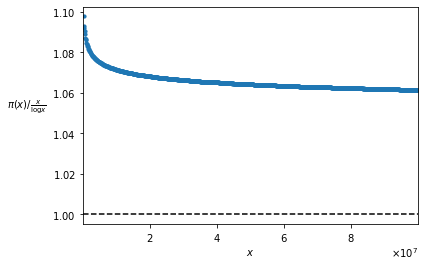
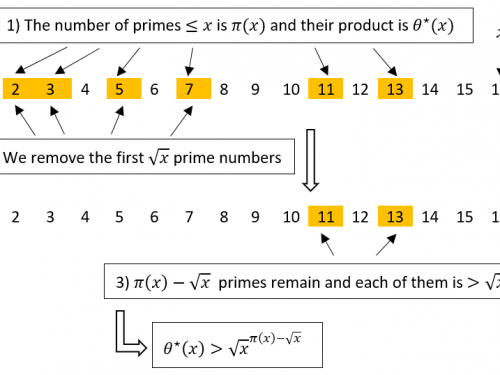
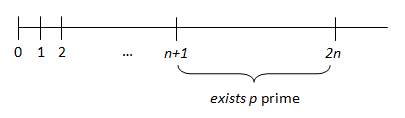
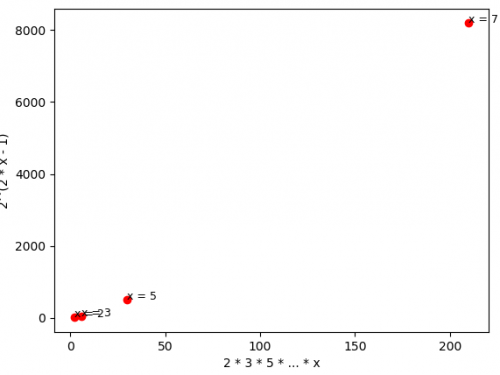
After almost three centuries, will we find a proof?













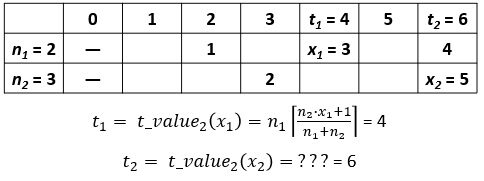


Seamless Theme Keith, made by Altervista
Create a website and earn with Altervista - Disclaimer - Report Abuse - Privacy Policy - Customize advertising tracking