Prerequirements:
We saw that the functions \theta^{\star}(x) and \psi^{\star}(x) behave in opposite manners. In fact, comparing Proposition N.3 (Underestimation of \psi^{\star}(x)) with Proposition N.1 (Majorization of the product of primes up to x) you can see that, while \psi^{\star}(x) is suited to be underestimated, \theta^{\star}(x) is suited to be overestimated. The same thing happens when the function \pi(x) is introduced: we saw in the Corollary of Proposition N.2 that \psi^{\star}(x) can be overestimated by an expression containing \pi(x); in the same way, now we’ll see how \theta^{\star}(x) can be underestimated by a similar expression.
Let’s fix an integer x and suppose that x \gt 1, so there exists at least one prime number up to x. An obvious way for underestimating the function \theta^{\star} consists in excluding some of the primes involved in its calculation, that is considering the product of a subset of them. But which should be excluded? As we are making an underestimation, the more the value is big, i.e. the more it’s close to \theta^{\star}(x), the more it’s good. So the best possible underestimation can be obtained by excluding the smallest primes: you can easily understand this with an example, like \theta^{\star}(7) = 2 \cdot 3 \cdot 5 \cdot 7: if we exclude from the product one prime number, out of the four possible products (3 \cdot 5 \cdot 7, 2 \cdot 5 \cdot 7, 2 \cdot 3 \cdot 7 and 2 \cdot 3 \cdot 5), the biggest is just that one obtained by excluding the smallest prime, that is 3 \cdot 5 \cdot 7.
This is the principle at the base of the underestimation of \theta^{\star}: from the complete product the smallest prime factors are excluded, and then an underestimation of the product of the remaining ones is looked for. In this way Lemma N.3 is obtained.
Underestimation of \theta^{\star}(x) through \pi(x)
For every real number \delta \geq 0 and for every x \gt 1:
We can optionally include the case x = 1 by putting \geq in place of \gt. However this is of little importance, because we are interested in big values of x.
We saw that, in order to obtain a good underestimation, it’s convenient to exclude, from the product of primes up to x, the smaller ones, starting from 2 up to a certain p_i. But what is this p_i? Where do we have to stop in excluding primes? Naturally this number depends on x, just like the total number of prime factors, which is \pi(x). The most obvious choices in this case are \delta x or x^\delta, for some constant \delta. For example, for \delta = \frac{1}{2}, we can choose to exclude the first \frac{x}{2} or the first x^{\frac{1}{2}} = \sqrt{x} prime numbers (supposing for the moment, for simplicity, these numbers to be integer). Experience teaches that the second choice is the most convenient. The reason is rather subtle and we’ll see it in the next post. For the moment we establish to exclude, from the product \theta^{\star}(x), the first \sqrt{x} prime numbers. Making so, the number of considered primes decreases from \pi(x) to \pi(x) - \sqrt{x}. All this of course makes sense only if \sqrt{x} \leq \pi(x), a limit case in which all factors would be excluded, obtaining a product of zero factors that, as we agreed, is 1. Surely we cannot have \sqrt{x} \gt \pi(x): we cannot eliminate more factors than we have. But it’s not convenient to get lost in these details: let’s go on supposing that \sqrt{x} \leq \pi(x) and finally we’ll see if the conclusion we’ll reach is valid also if this supposition was false.
Now, observing the \pi(x) - \sqrt{x} remaining factors, we can note that each of them is greater than \sqrt{x}. This follows by a general principle. In a finite strictly increasing sequence of positive integers 0 \lt a_1 \lt a_2 \lt \ldots \lt a_{n-1} \lt a_n, the i-th element a_i is greater or equal to i (in fact a_1 \gt 0 \implies a_1 \geq 1, a_2 \gt a_1 \geq 1 \implies a_2 \geq 2, etcetera). So if we exclude the first k elements, a_1, a_2, \ldots, a_{k}, the remaining elements a_{k+1}, \ldots, a_{n-1}, a_{n} will be all greater than k. In fact, by the previous argument, a_{k+1} \geq k+1 \gt k and the next elements will be greater than k too because the sequence is increasing. In our case the strictly increasing sequence is the one of the prime numbers less than or equal to x: 2, 3, \ldots, p_{\pi(x) - 1}, p_{\pi(x)}, and the number k is \sqrt{x}. After the removal, the smallest remaining prime will be p_{\sqrt{x} + 1} and, by this simple principle, we can be sure that it will be greater than \sqrt{x}, just like all the other remaining primes, that will be even greater.
Summarizing, after the removal \pi(x) - \sqrt{x} prime factors remain, each greater than \sqrt{x}. Hence their product is greater than
Moreover, being the product of the remaining factors lower than the complete product, that is \theta^{\star}(x), we have that
All the argument that brought to formula (1) is summarized in the following picture.
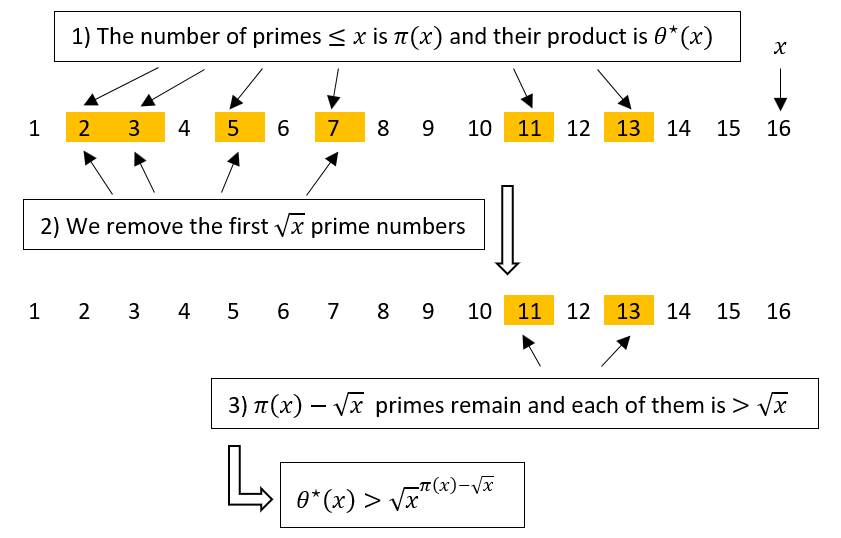
If we now reconsider the hypothesis that \sqrt{x} \leq \pi(x), we see that it’s not so important, because formula (1) is valid in any case: if \sqrt{x} \gt \pi(x), the exponent is negative and the number \sqrt{x}^{\pi(x) - \sqrt{x}} is less than 1, and so also less than \theta^{\star}(x), that is at least 1 (recall in fact that \theta^{\star}(1) = 1). The hypothesis of \sqrt{x} to be integer is not essential too: otherwise the number of prime factors to exclude will be \left \lfloor \sqrt{x} \right \rfloor, those ones remaining would be greater than \left \lfloor \sqrt{x} \right \rfloor, so at least \left \lfloor \sqrt{x} \right \rfloor + 1 and so greater than \sqrt{x}, and formula (1) would become
from which (1) is obtained again.
This approximation may seem rough for how we obtained it, but it hides a big potential. In fact the argument we carried on with the square root of x, that is x^{\frac{1}{2}}, can be repeated in a similar way with any other power of x with real exponent \delta \geq 0 (we do not consider negative powers because in this case x^{\delta} would be less than 1, so we would not exclude any prime and the reasoning above would be valid no more). Thanks to this last remark we just obtain Lemma N.3.
As an example, let’s apply the Lemma for x = 64 and for two values of \delta, \delta = \frac{1}{3} and \delta = \frac{1}{2}:
Both, by Lemma N.3, are underestimations of \theta^{\star}(64) = 117.288.381.359.406.970.983.270. The second is a bit closer to the actual value, but they are both very faraway. Yet, as we’ll see in the next posts, this kind of approxination is enough for telling something interesting about prime numbers.