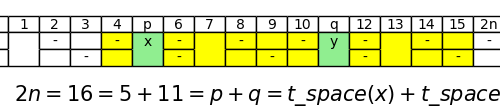
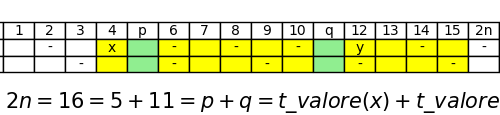
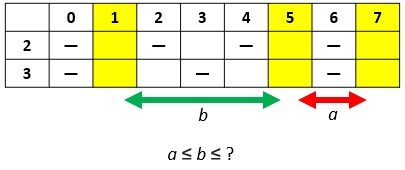
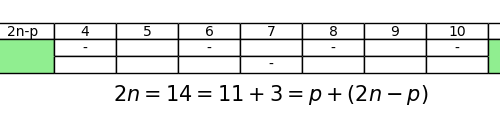
Our research
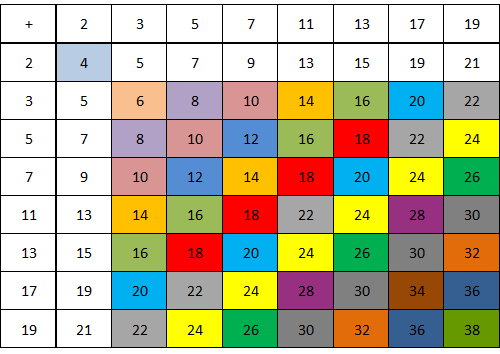
Currently, there are several attempts to prove the Goldbach's conjecture, which are complete, in the sense that they come to…
After almost three centuries, will we find a proof?









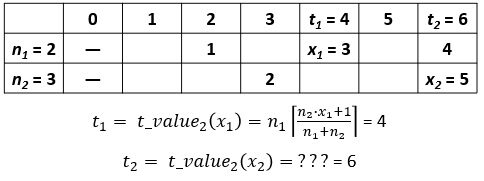


Seamless Theme Keith, made by Altervista
Create a website and earn with Altervista - Disclaimer - Report Abuse - Privacy Policy - Customize advertising tracking