
Our proof strategies: an overview
Prerequisite: Goldbach’s conjecture As already indicated, our ultimate goal is to use dashed line theory to prove Goldbach’s conjecture. Dashed…
After almost three centuries, will we find a proof?



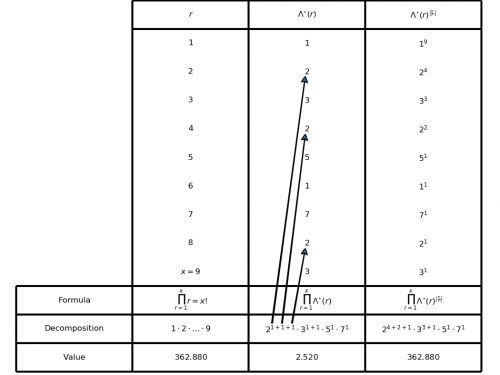
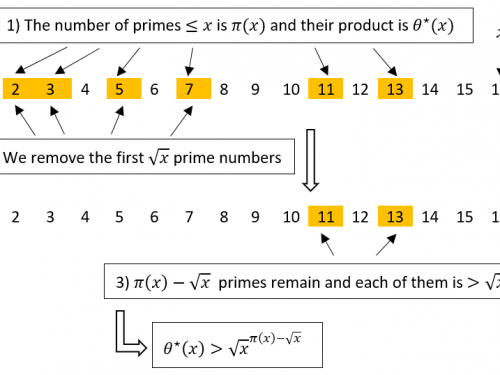
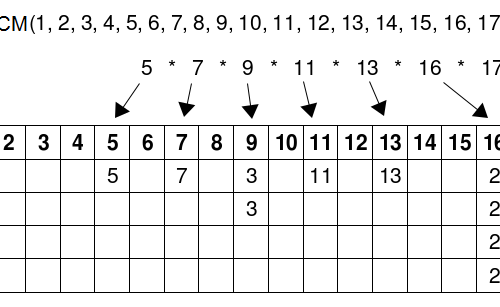

Seamless Theme Keith, made by Altervista
Create a website and earn with Altervista - Disclaimer - Report Abuse - Privacy Policy - Customize advertising tracking