La dimostrazione della congettura di Goldbach è uno dei più grandi problemi ancora irrisolti che riguardano i numeri primi. Inizialmente formulata nel 1742 dal matematico Christian Goldbach, dal quale prende il nome, è stata riformulata da Eulero nella forma in cui la conosciamo oggi:
Ogni numero pari maggiore di 2 può essere scritto come somma di due numeri primi.
Nonostante l'evidenza empirica e la semplicità dell'enunciato, la congettura resiste a tutti i tentativi di dimostrazione da quasi tre secoli. Tuttavia, diversi matematici hanno dimostrato delle versioni della congettura meno forti.
L'affermazione formulata da Christian Goldbach è una "congettura", quindi, in linea di principio, si tratta di un'ipotesi. Ciò vuol dire che potrebbe essere:
- Vera, ossia tutti i numeri pari maggiori di 2 sono esprimibili come somma di due numeri primi;
- Falsa, ossia esiste almeno un numero pari maggiore di 2 che non si può scrivere come somma di due numeri primi.
Attualmente esistono diversi tentativi di dimostrazione della congettura di Goldbach, che sono completi, nel senso che arrivano alla conclusione, ma contengono una serie di problemi, per cui non sono stati considerati validi dalla comunità internazionale. Noi proponiamo invece alcune strategie dimostrative, che sono ancora lungi dal diventare dimostrazioni complete, ma già hanno portato a dei risultati intermedi interessanti e finora non confutati. Speriamo che questo materiale possa costituire un utile spunto per chi si è messo, come noi, alla ricerca della dimostrazione...
L'affermazione formulata da Christian Goldbach è una "congettura", quindi, in linea di principio, si tratta di un'ipotesi. Ciò vuol dire che potrebbe essere:
- Vera, ossia tutti i numeri pari maggiori di 2 sono esprimibili come somma di due numeri primi;
- Falsa, ossia esiste almeno un numero pari maggiore di 2 che non si può scrivere come somma di due numeri primi.
La congettura di Goldbach si colloca nell'ambito della Teoria dei numeri, la branca della matematica che studia i numeri interi. Per comprendere le dimostrazioni dei risultati simili alla congettura, e molto probabilmente anche per dimostrare la congettura stessa, sono richieste solide conoscenze di teoria dei numeri. Queste conoscenze, però, raramente entrano a par parte del curriculum di studi di un matematico...
La teoria dei tratteggi è una nuova teoria matematica che studia il rapporto tra la successione dei numeri naturali e la loro relazione di divisibilità. Problemi tipici sono il calcolo dell'n-esimo numero naturale divisibile per almeno uno di k numeri fissati, o non divisibile per alcuno di essi. Per tale natura, la teoria si presta allo studio dei numeri primi mediante un approccio costruttivo, ispirato al crivello di Eratostene...
La congettura di Goldbach si colloca nell'ambito della Teoria dei numeri, la branca della matematica che studia i numeri interi. Per comprendere le dimostrazioni dei risultati simili alla congettura, e molto probabilmente anche per dimostrare la congettura stessa, sono richieste solide conoscenze di teoria dei numeri. Queste conoscenze, però, raramente entrano a par parte del curriculum di studi di un matematico...
La teoria dei tratteggi è una nuova teoria matematica che studia il rapporto tra la successione dei numeri naturali e la loro relazione di divisibilità. Problemi tipici sono il calcolo dell'n-esimo numero naturale divisibile per almeno uno di k numeri fissati, o non divisibile per alcuno di essi. Per tale natura, la teoria si presta allo studio dei numeri primi mediante un approccio costruttivo, ispirato al crivello di Eratostene...
Ultimi articoli
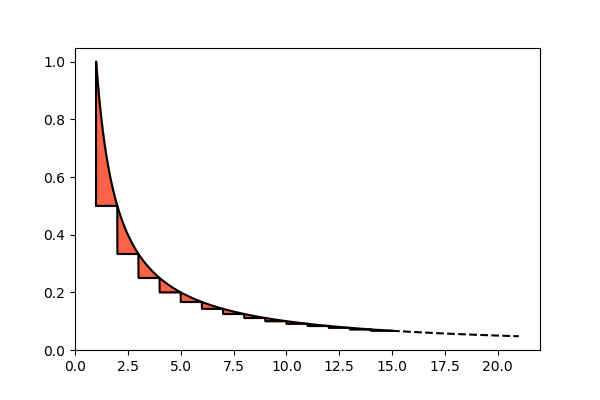
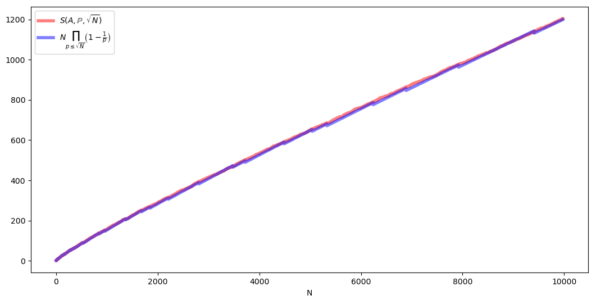
Nell'articolo precedente abbiamo calcolato la funzione di crivello del crivello di Eratostene partendo dall'algoritmo, ottenendo una formula con un numero di termini che cresce in modo esponenziale rispetto al numero di primi utilizzati, perciò troppo complessa per poter essere utilizzata in pratica. Però in fin dei conti non è necessario calcolare esattamente una funzione di crivello: per poterla studiare (ad esempio per capirne l'andamento asintotico) sarebbe sufficiente trovare una buona approssimazione. Se quindi ci accontentassimo di approssimare la funzione di crivello, nel caso del crivello di Eratostene, otterremmo una formula meno complicata? Quanto sarebbe buona l'approssimazione? In questo articolo risponderemo…
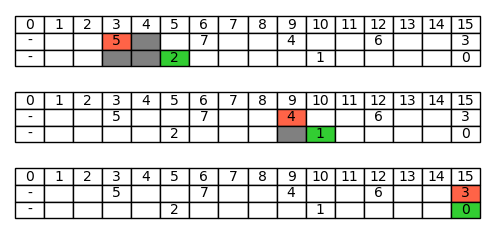
Nell'articolo precedente abbiamo esaminato nel dettaglio il crivello di Eratostene, sia a livello algoritmico che come funzione di crivello. Abbiamo visto che tra le due formulazioni c'è un forte legame, in quanto la funzione di crivello calcola quanti elementi restano nell'insieme {2, 3, 4, ..., N} dopo aver applicato l'algoritmo. Ma allora, per calcolare la funzione di crivello, perché non partire proprio dallo studio dall'algoritmo da cui essa trae origine? In questo articolo e nel successivo vedremo che quest'idea non funziona nella pratica, e capiremo il perché.
Come abbiamo visto, nella formula del crivello di Selberg compaiono dei parametri λd, che vengono utilizzati sia nella stima della funzione di crivello che nel relativo termine di errore. In questo articolo calcoleremo questi parametri in modo da ottenere una stima più bassa possibile.
In quest’articolo cominceremo a entrare nel vivo della teoria dei crivelli, analizzando nel dettaglio il cosiddetto “crivello di Selberg”. Non si tratta, in realtà di un nuovo crivello (paragonabile ad esempio a quello di Eratostene); il crivello (inteso come funzione) è sempre quello generale, è la sua maggiorazione che è di Selberg. In sintesi, possiamo dire che il crivello di Selberg è un modo di maggiorare una funzione di crivello con una funzione semplice da calcolare, composta da due termini: una stima e un termine di errore.
Nell'articolo precedente abbiamo visto che la dimostrazione del Teorema di Chen si basa sulla teoria dei crivelli. Ma che cos'è un crivello? In questo articolo lo spiegheremo basandoci sull'esempio più famoso di crivello, quello di Eratostene. Esso permette di rispondere a una semplice domanda: dato un numero intero N ≥ 2, quali sono i numeri primi minori o uguali di N?