Prerequisiti:
- Il crivello di Eratostene e la definizione formale di crivello
- La funzione di Möbius e la sua connessione con la funzione Λ
Nell’articolo precedente abbiamo esaminato nel dettaglio il crivello di Eratostene, sia a livello algoritmico che come funzione di crivello. Abbiamo visto che tra le due formulazioni c’è un forte legame, in quanto la funzione di crivello calcola quanti elementi restano nell’insieme \{2, 3, 4, \ldots, N\} dopo aver applicato l’algoritmo. Ma allora, per calcolare la funzione di crivello, perché non partire proprio dallo studio dall’algoritmo da cui essa trae origine? In questo articolo e nel successivo vedremo che quest’idea non funziona nella pratica, e capiremo il perché.
Dall’algoritmo del crivello di Eratostene al calcolo della corrispondente funzione di crivello
Dato un intero N \gt 1, consideriamo l’insieme A := \{1, 2, 3, \ldots, N\} e supponiamo di eseguire su di esso l’algoritmo previsto dal crivello di Eratostene, nella versione che cancella tutti i multipli di un primo p, compreso p stesso (anche se sappiamo che questa non è la versione più comune del crivello di Eratostene, ma è una semplificazione utile per il seguito). Diversamente dall’articolo precedente, questa volta abbiamo incluso anche 1 nell’insieme di partenza per semplificare alcune formule che vedremo tra poco, ma la sostanza non cambia: alla fine rimarranno in A solamente i numeri non divisibili per nessun primo minore o uguale di \sqrt{N}, cioè 1 e tutti i numeri primi maggiori di \sqrt{N}. Utilizzando la definizione di funzione di crivello, possiamo indicare il numero di tali primi con la seguente notazione:
Questo numero può essere ricavato seguendo passo passo l’algoritmo del crivello di Eratostene, partendo dal numero di elementi iniziale e sottraendo man mano il numero di elementi eliminati in ciascun passaggio:
- Inizialmente l’insieme A contiene tutti gli interi da 1 a N, quindi |A| = N.
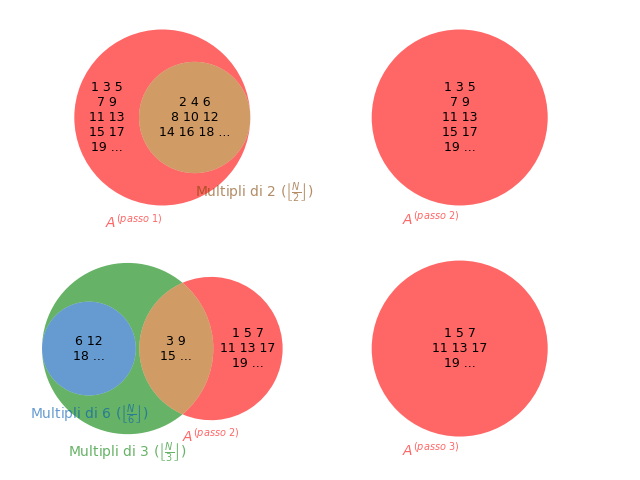
- Per prima cosa il crivello di Eratostene elimina da A tutti i multipli di 2. Gli elementi eliminati saranno quindi 2, 4, 6, …, N se N è pari; 2, 4, 6, …, N - 1 se N è dispari: in totale, sono \frac{N}{2} elementi se N è pari e \frac{N - 1}{2} se N è dispari.
Accorpando i due casi, possiamo dire l’algoritmo eliminerà \left\lfloor \frac{N}{2} \right\rfloor elementi (dove \left\lfloor \right\rfloor è la parte intera approssimata per difetto), dato che il risultato di questa formula coincide appunto con \frac{N}{2} se N è pari e con \frac{N - 1}{2} se N è dispari. Quindi, qualunque sia N, dopo aver eliminato tutti i multipli di 2, in A saranno rimasti N - \left\lfloor \frac{N}{2} \right\rfloor elementi. - Successivamente il crivello di Eratostene elimina da A tutti i multipli di 3. I numeri eliminati non saranno però 3, 6, 9, 12, …, perché alcuni di essi, ad esempio 6, saranno già stati eliminati in precedenza, in quanto divisibili anche per 2. Però, per calcolare quanti multipli di 3 vengono eliminati, possiamo effettuare due passaggi:
- prima contiamo tutti i multipli di 3 minori o uguali di N (ossia quanti ce n’erano nell’insieme A iniziale, prima del passaggio precedente);
- dal numero ottenuto, sottraiamo il numero di multipli di 6 minori o uguali di N; infatti essi, essendo divisibili anche per 2, sono già stati eliminati in precedenza e non devono essere riconteggiati.
In generale, il numero di multipli positivi di un certo numero naturale k che sono minori o uguali di N è \left\lfloor \frac{N}{k} \right\rfloor, com’è facile dimostrare; quindi il numero di multipli di 3 e il numero di multipli di 6 minori o uguali di N sono dati rispettivamente dalle formule \left\lfloor \frac{N}{3} \right\rfloor e \left\lfloor \frac{N}{6} \right\rfloor. Per cui, in base ai due punti precedenti, il numero di elementi eliminati in questo passaggio è \left\lfloor \frac{N}{3} \right\rfloor - \left\lfloor \frac{N}{6} \right\rfloor. Quindi, se dopo l’eliminazione dei multipli di 2 erano rimasti N - \left\lfloor \frac{N}{2} \right\rfloor elementi in A, dopo aver eliminato anche i multipli di 3 ne resteranno N - \left\lfloor \frac{N}{2} \right\rfloor - \left( \left\lfloor \frac{N}{3} \right\rfloor - \left\lfloor \frac{N}{6} \right\rfloor \right) = N - \left\lfloor \frac{N}{2} \right\rfloor - \left\lfloor \frac{N}{3} \right\rfloor + \left\lfloor \frac{N}{6} \right\rfloor.
- Successivamente, il crivello di Eratostene elimina da A tutti i multipli di 5. Dobbiamo considerare però che i multipli di 5 divisibili per 2 o per 3 o per entrambi sono già stati eliminati, per cui potremmo ragionare come segue:
- prima contiamo tutti i multipli di 5 minori o uguali di N;
- dal numero ottenuto, sottraiamo il numero di multipli di 10 minori o uguali di N; infatti essi, essendo divisibili anche per 2, sono già stati eliminati in precedenza;
- dal numero ottenuto, sottraiamo il numero di multipli di 15 minori o uguali di N; infatti essi, essendo divisibili anche per 3, sono già stati eliminati in precedenza.
Ora però la questione diventa più complessa perché, se ci fermassimo qui, toglieremmo due volte (nei punti b. e c.) i multipli di 30, ossia i multipli di 5 che sono divisibili anche contemporaneamente per 2 e per 3. Per correggere questa doppia eliminazione, possiamo aggiungere un ulteriore passaggio:
- prima contiamo tutti i multipli di 5 presenti minori o uguali di N;
- dal numero ottenuto, sottraiamo il numero di multipli di 10 minori o uguali di N; infatti essi, essendo divisibili anche per 2, sono già stati eliminati in precedenza;
- dal numero ottenuto, sottraiamo il numero di multipli di 15 minori o uguali di N; infatti essi, essendo divisibili anche per 3, sono già stati eliminati in precedenza;
- al numero ottenuto, aggiungiamo il numero di multipli di 30 minori o uguali di N; infatti essi, essendo divisibili anche per 2 e 3, sono stati sottratti due volte nei passaggi precedenti, mentre devono essere sottratti una volta sola.
Quindi il numero di multipli di 5 eliminati da A è \left\lfloor \frac{N}{5} \right\rfloor - \left\lfloor \frac{N}{10} \right\rfloor - \left\lfloor \frac{N}{15} \right\rfloor + \left\lfloor \frac{N}{30} \right\rfloor. Il procedimento è rappresentato nell’immagine seguente:
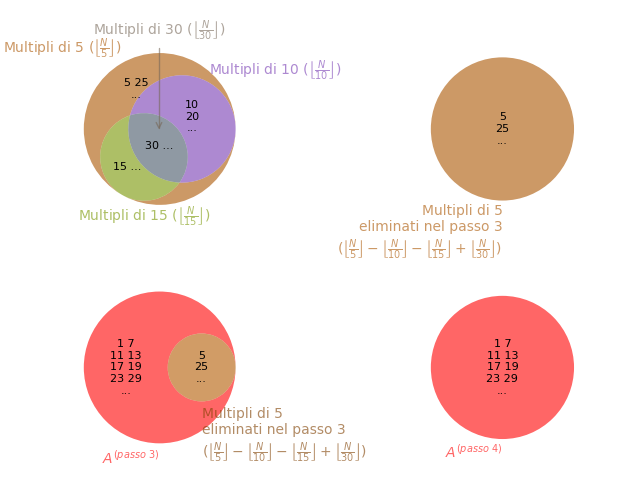
Figura 2: eliminazione dei multipli di 5 dall’insieme degli interi da 1 a N già privato dei multipli di 2 e di 3. Nel calcolo del numero di multipli di 5 da eliminare (prima riga), il numero di multipli di 30 va aggiunto alla formula per compensare la doppia sottrazione, sia come parte dei multipli di 10 che come parte dei multipli di 15. Il numero di elementi di A prima di questo passaggio era:
N - \left\lfloor \frac{N}{2} \right\rfloor - \left\lfloor \frac{N}{3} \right\rfloor + \left\lfloor \frac{N}{6} \right\rfloorQuindi, dopo aver eliminato anche i multipli di 5, il numero di elementi di A diventa:
\begin{aligned} N - \left\lfloor \frac{N}{2} \right\rfloor - \left\lfloor \frac{N}{3} \right\rfloor + \left\lfloor \frac{N}{6} \right\rfloor - \left( \left\lfloor \frac{N}{5} \right\rfloor - \left\lfloor \frac{N}{10} \right\rfloor - \left\lfloor \frac{N}{15} \right\rfloor + \left\lfloor \frac{N}{30} \right\rfloor \right) &= \\ N - \left\lfloor \frac{N}{2} \right\rfloor - \left\lfloor \frac{N}{3} \right\rfloor + \left\lfloor \frac{N}{6} \right\rfloor - \left\lfloor \frac{N}{5} \right\rfloor + \left\lfloor \frac{N}{10} \right\rfloor + \left\lfloor \frac{N}{15} \right\rfloor - \left\lfloor \frac{N}{30} \right\rfloor &= \\ N - \left\lfloor \frac{N}{2} \right\rfloor - \left\lfloor \frac{N}{3} \right\rfloor - \left\lfloor \frac{N}{5} \right\rfloor + \left\lfloor \frac{N}{6} \right\rfloor + \left\lfloor \frac{N}{10} \right\rfloor + \left\lfloor \frac{N}{15} \right\rfloor - \left\lfloor \frac{N}{30} \right\rfloor \end{aligned} \tag{2} - Come sappiamo, l’algoritmo del crivello di Eratostene prosegue fino all’eliminazione dei multipli dell’ultimo numero primo da considerare, ossia il più grande numero primo minore o uguale di \sqrt{N}. Nei successivi passi di eliminazione si ragiona allo stesso modo dei passi precedenti ma, come si può immaginare, le formule diventano sempre più complicate.
Questi primi due passaggi sono rappresentati nell’immagine seguente:
Alla base del ragionamento sopra esposto vi è un principio più generale, chiamato principio di inclusione-esclusione, che però non serve conoscere per i nostri scopi, quindi lasciamo questo approfondimento a discrezione dei nostri lettori.
Riprendendo gli esempi dell’articolo precedente, supponiamo che N = 32. Confrontiamo passo passo le nostre formule con gli elementi effettivamente eliminati dal crivello di Eratostene ad ogni passaggio:
- Inizialmente A = \{1, 2, 3, 4, \ldots, 32\}.
- I multipli di 2 da eliminare sono 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30 e 32; in totale sono 16 = \left\lfloor \frac{32}{2} \right\rfloor elementi. Quindi dopo questo passaggio l’insieme A avrà un numero di elementi uguale a:
\begin{aligned} |A| - |\{2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32\}| &= \\ 32 - \left\lfloor \frac{32}{2} \right\rfloor &= \\ 32 - 16 &= \\ 16 \end{aligned} \tag{a}
Infatti, al termine di questo passaggio, A = \{1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31\}, quindi abbiamo 16 elementi.
- I multipli di 3 da eliminare nel nuovo insieme A sono 3, 9, 15, 21 e 27. Questi 5 elementi sono dati dall’insieme di tutti i multipli di 3 minori o uguali di 32 (\{3, 6, 9, 12, 15, 18, 21, 24, 27, 30\}) dal quale però bisogna togliere l’insieme dei multipli di 6 (\{6, 12, 18, 24, 30\}):
\begin{aligned} \{3, 9, 15, 21, 27\} &= \\ \{3, 6, 9, 12, 15, 18, 21, 24, 27, 30\} \setminus \{6, 12, 18, 24, 30\} \end{aligned}
da cui, passando alle cardinalità:
\begin{aligned} |\{3, 9, 15, 21, 27\}| &= \\ |\{3, 6, 9, 12, 15, 18, 21, 24, 27, 30\}| - |\{6, 12, 18, 24, 30\}| &= \\ \left\lfloor \frac{32}{3} \right\rfloor - \left\lfloor \frac{32}{6} \right\rfloor &= \\ 10 - 5 &= \\ 5 \end{aligned} \tag{b}Il nuovo numero di elementi di A sarà quindi:
\begin{aligned} |\{1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31\}| - |\{3, 9, 15, 21, 27\}| &= \text{[per la (a)]} \\ 32 - \left\lfloor \frac{32}{2} \right\rfloor - |\{3, 9, 15, 21, 27\}| &= \text{[per la (b)]} \\ 32 - \left\lfloor \frac{32}{2} \right\rfloor - \left( \left\lfloor \frac{32}{3} \right\rfloor - \left\lfloor \frac{32}{6} \right\rfloor \right) &= \\ 32 - \left\lfloor \frac{32}{2} \right\rfloor - \left\lfloor \frac{32}{3} \right\rfloor + \left\lfloor \frac{32}{6} \right\rfloor &= \\ 32 - 16 - 10 + 5 &= \\ 11 \end{aligned} \tag{c}Infatti, al termine di questo passaggio, A = \{1, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31\}, quindi abbiamo 11 elementi.
- Nel nuovo insieme A ci sono solo due multipli di 5: 5 e 25. Essi si possono ottenere con la seguente operazione insiemistica:
\begin{aligned} \{5, 25\} &= \\ \{5, 10, 15, 20, 25, 30\} \setminus \{10, 20, 30\} \setminus \{15, 30\} \end{aligned}
cioè l’insieme dei multipli di 5, meno l’insieme dei multipli di 10, per considerare i multipli di 2 già tolti, meno l’insieme dei multipli di 15, per considerare i multipli di 3 già tolti. Però, passando alle cardinalità, abbiamo un’inconsistenza:
\begin{aligned} |\{5, 25\}| &\neq \\ |\{5, 10, 15, 20, 25, 30\}| - |\{10, 20, 30\}| - |\{15, 30\}| \end{aligned}Infatti il secondo e il terzo insieme non sono disgiunti ma hanno il 30 in comune, per cui quest’ultimo nell’espressione a destra viene conteggiato due volte col segno meno. Per conteggiarlo una volta sola, ristabilendo l’uguaglianza, dobbiamo aggiungere il conteggio degli elementi comuni agli ultimi due insiemi (in questo caso solo 30):
\begin{aligned} |\{5, 25\}| &= \\ |\{5, 10, 15, 20, 25, 30\}| - |\{10, 20, 30\}| - |\{15, 30\}| + |\{30\}| &= \\ 6 - 3 - 2 + 1 &= \\ 2 \end{aligned}Ma i quattro insiemi al secondo passaggio non solo altro che, rispettivamente, i multipli di 5, di 10, di 15 e di 30, per cui le loro cardinalità sono date rispettivamente dalle formule \left\lfloor \frac{32}{5} \right\rfloor, \left\lfloor \frac{32}{10} \right\rfloor, \left\lfloor \frac{32}{15} \right\rfloor e \left\lfloor \frac{32}{30} \right\rfloor. Sommando algebricamente il tutto, il numero di multipli di 5 rimossi dall’algoritmo in questo passaggio (cioè solo 5 e 25) è dato dalla formula:
\begin{aligned} |\{5, 25\}| &= \\ \left\lfloor \frac{32}{5} \right\rfloor - \left\lfloor \frac{32}{10} \right\rfloor - \left\lfloor \frac{32}{15} \right\rfloor + \left\lfloor \frac{32}{30} \right\rfloor \end{aligned} \tag{d}Il nuovo numero di elementi di A sarà quindi:
\begin{aligned} |\{1, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31\}| - |\{5, 25\}| &= \text{[per la (c)]} \\ 32 - \left\lfloor \frac{32}{2} \right\rfloor - \left\lfloor \frac{32}{3} \right\rfloor + \left\lfloor \frac{32}{6} \right\rfloor - |\{5, 25\}| &= \text{[per la (d)]} \\ 32 - \left\lfloor \frac{32}{2} \right\rfloor - \left\lfloor \frac{32}{3} \right\rfloor + \left\lfloor \frac{32}{6} \right\rfloor - \left(\left\lfloor \frac{32}{5} \right\rfloor - \left\lfloor \frac{32}{10} \right\rfloor - \left\lfloor \frac{32}{15} \right\rfloor + \left\lfloor \frac{32}{30} \right\rfloor \right) &= \\ 32 - \left\lfloor \frac{32}{2} \right\rfloor - \left\lfloor \frac{32}{3} \right\rfloor - \left\lfloor \frac{32}{5} \right\rfloor + \left\lfloor \frac{32}{6} \right\rfloor + \left\lfloor \frac{32}{10} \right\rfloor + \left\lfloor \frac{32}{15} \right\rfloor - \left\lfloor \frac{32}{30} \right\rfloor &= \\ 32 - 16 - 10 - 6 + 5 + 3 + 2 - 1 &= \\ 9\end{aligned}Infatti, al termine di questo passaggio, A = \{1, 7, 11, 13, 17, 19, 23, 29, 31\}, quindi abbiamo 9 elementi.
- Il crivello di Eratostene termina qui, perché 5 è il più grande numero primo minore o uguale di \sqrt{32}.
Ricapitolando, possiamo dire quindi che la formula
calcola correttamente il numero di elementi dell’insieme A iniziale che non sono divisibili né per 2, né per 3 e né per 5. Quindi, per definizione di funzione di crivello, possiamo dire che:
La formula generale del crivello di Eratostene
Possiamo notare che la formula (2) è una somma algebrica di espressioni del tipo \left\lfloor \frac{N}{d} \right\rfloor, col segno negativo se d è il prodotto di un numero dispari di numeri primi, e col segno positivo se d è il prodotto di un numero pari di numeri primi. Il primo termine, N, non fa eccezione, perché possiamo intenderlo come \left\lfloor \frac{N}{1} \right\rfloor, dove 1 è il prodotto di zero numeri primi, quindi di un numero pari di numeri primi. Inoltre d è sempre il prodotto di fattori primi distinti (equivalentemente, è privo di quadrati). Vale anche il viceversa: per ogni possibile prodotto d di zero o più numeri primi distinti, scelti nell’insieme \{2, 3, 5\} dei numeri primi considerati nel crivello, abbiamo un termine del tipo \left\lfloor \frac{N}{d} \right\rfloor.
Questa regola diventa sempre più evidente al crescere del numero di primi utilizzati nel crivello. Ad esempio, se eliminassimo da A anche i multipli di 7, il numero di elementi restanti sarebbe dato dalla formula seguente:
In questa espressione abbiamo raggruppato i termini \left\lfloor \frac{N}{d} \right\rfloor su righe diverse in base al numero di fattori primi che rientrano nella fattorizzazione di d:
- sulla prima riga troviamo il termine con d = 1, essendo 1 il prodotto di 0 numeri primi, con segno positivo perché 0 è pari;
- sulla seconda riga d è un numero primo scelto nell’insieme \{2, 3, 5, 7\} e i termini hanno segno negativo perché 1 è dispari;
- sulla terza riga abbiamo tutti i possibili termini dove d è il prodotto di 2 numeri primi distinti scelti dallo stesso insieme, e i termini hanno segno positivo perché 2 è pari;
- i numeri primi distinti che costituiscono d diventano 4 sulla quarta riga, con i termini di segno negativo;
- infine, sull’ultima riga, abbiamo l’unico possibile prodotto di quattro numeri primi distinti scelti dall’insieme \{2, 3, 5, 7\}, ossia d = 2 \cdot 3 \cdot 5 \cdot 7 = 210, e il segno del termine è positivo.
La formula contiene complessivamente 16 = 2^4 termini. In generale, dato un intero k \gt 0, possiamo considerare l’insieme dei primi k numeri primi e ottenere, partendo da esso, una formula strutturalmente analoga alle formule (2) e (3) (nelle quali k è rispettivamente 3 e 4):
Formula generale del crivello di Eratostene
Sia N \gt 1 un intero e sia k il numero di numeri primi minori o uguali di \sqrt{N}. Si consideri la formula definita dalle seguenti proprietà:
- La formula è una somma algebrica di termini del tipo \pm \left\lfloor \frac{N}{d} \right\rfloor, dove d è un prodotto di zero o più numeri primi distinti scelti nell’insieme dei primi k numeri primi;
- Per ogni possibile prodotto di numeri primi distinti scelti nell’insieme dei primi k numeri primi, è presente uno e un solo termine del tipo \pm \left\lfloor \frac{N}{d} \right\rfloor;
- Il segno di ciascun termine \pm \left\lfloor \frac{N}{d} \right\rfloor è positivo se d è il prodotto di un numero pari di numeri primi; negativo se d è il prodotto di un numero dispari di numeri primi.
Chiameremo tale formula formula generale del crivello di Eratostene con numero di partenza N.
È facile dimostrare che vale la seguente Proprietà:
Numero di termini della formula generale del crivello di Eratostene
Per ogni N \gt 1, posto k il numero di numeri primi minori o uguali di \sqrt{N}, la formula generale del crivello di Eratostene con numero di partenza N ha 2^k termini.
Per definizione, la formula generale del crivello di Eratostene contiene, a meno del segno, tutti i possibili termini del tipo \left\lfloor \frac{N}{d} \right\rfloor, dove d è un prodotto di zero o più numeri primi scelti nell’insieme dei primi k numeri primi, senza ripetizioni. Possiamo rappresentare un tale d come una k-upla (a_1, a_2, \ldots, a_k), dove ciascun elemento a_i può essere 1 o 0, a seconda che l’i-esimo numero primo compaia o no nella fattorizzazione di d. Ad esempio, se k = 4, come nella formula (3), il numero 10 sarebbe rappresentato con la quadrupla (1, 0, 1, 0), perché è il prodotto del primo numero primo per il terzo numero primo; il numero 35 sarebbe rappresentato con la quadrupla (0, 0, 1, 1), perché è il prodotto del terzo e del quarto numero primo; i numeri 1 e 210 sarebbero rappresentati rispettivamente dalle quadruple (0, 0, 0, 0) e (1, 1, 1, 1), perché sono rispettivamente il prodotto di nessun numero primo e di tutti i primi quattro numeri primi.
È evidente che ogni k-upla determina uno e un solo numero d (basta calcolare il prodotto dei corrispondenti numeri primi) e, viceversa, ogni numero d ha una e una sola k-upla corrispondente (per ottenerla, basta vedere quali primi sono presenti nella sua fattorizzazione). Esiste, in altri termini, una corrispondenza biunivoca tra l’insieme dei possibili d e quello delle possibili k-uple formate da valori binari (0 o 1), quindi la cardinalità dei due insiemi dev’essere la stessa. Ma le possibili k-uple sono 2^k, perché esistono due scelte per la prima posizione, per ogni scelta della prima posizione esistono due possibili scelte per la seconda posizione, e così via fino alla k-esima posizione, per cui in totale esistono \underbrace{2 \cdot 2 \cdot \ldots \cdot 2}_{k \text{ volte}} = 2^k possibili k-uple. Allora anche i possibili d saranno 2^k e, dato che ogni d determina un singolo termine della formula generale, quest’ultima conterrà 2^k termini.
È proprio questa crescita esponenziale del numero di termini che rende l’algoritmo del crivello di Eratostene poco utile per il calcolo della corrispondente funzione di crivello.
Questo potrebbe sembrare un controsenso, perché anche un algoritmo è una forma di calcolo; bisogna considerare però che il crivello di Eratostene è stato pensato per calcolare l’insieme dei numeri primi minori o uguali di N, non la cardinalità di questo insieme. È chiaro che, una volta calcolato l’insieme, diventa immediato calcolarne anche la cardinalità, ma ottenere una formula per calcolare direttamente la cardinalità senza passare dall’insieme è un problema di tipo diverso e, come abbiamo visto, l’approccio di partire da un algoritmo che calcola l’insieme non funziona in modo soddisfacente. Con l’eccezione di valori di k molto piccoli, è decisamente più conveniente applicare l’algoritmo del crivello di Eratostene così com’è e alla fine contare quanti elementi compaiono nel risultato, piuttosto che applicare la formula generale con 2^k termini, nonostante tale formula derivi dallo stesso algoritmo.
L’identità di Legendre
Fin qui abbiamo visto come a volte un approccio efficace dal punto di vista algoritmico può non esserlo dal punto di vista matematico. Non era questo, però, l’unico scopo di questo articolo. Fortunatamente l’approccio che abbiamo descritto finora ha una sua utilità teorica, infatti lo useremo come punto di partenza per la creazione di crivelli più sofisticati che vedremo nei prossimi articoli. A tal fine, però, conviene enunciare la formula generale in una forma opportuna, ottenendo la cosiddetta identità di Legendre.
Per arrivare all’identità di Legendre, possiamo partire dalla formula (3) e fare due considerazioni:
- Indicando come sempre con d il denominatore del generico termine della formula, possiamo osservare che questi d formano, nel complesso, l’insieme dei divisori di 210, che è il prodotto dei numeri primi utilizzati nella formula (210 = 2 \cdot 3 \cdot 5 \cdot 7). Infatti tutti i denominatori (1, 2, 3, 5, 7, 6, 10, 15, …) sono divisori di 210; viceversa, se d è un divisore di 210, esso è uno dei denominatori perché soddisfa il primo punto della Definizione C.2, ossia è il prodotto di numeri primi distinti scelti nell’insieme \{2, 3, 5, 7\}
Perché, se d è un divisore di 210, soddisfa il primo punto della Definizione C.2?
Se p è un fattore primo di d, che per ipotesi divide 210, p deve essere anche un fattore primo di 210, quindi p \in \{2, 3, 5, 7\}. Inoltre, p non può essere presente nella fattorizzazione di d più di una volta, altrimenti, essendo d un divisore di 210, sarebbe presente più volte anche nella fattorizzazione di 210, ma ciò non è possibile perché 210 è privo di quadrati. Quindi d è il prodotto di numeri primi distinti scelti nell’insieme \{2, 3, 5, 7\}.
- Abbiamo detto che il segno del generico termine \left\lfloor \frac{N}{d} \right\rfloor è positivo se d è il prodotto di un numero pari di numeri primi; negativo se d è il prodotto di un numero dispari di numeri primi. Ma esiste una funzione, ben nota in teoria dei numeri, che effettua proprio questo calcolo: è la funzione di Möbius, indicata col simbolo \mu. La definizione, che è approfondita nel percorso sul Teorema dei numeri primi, è la seguente
\mu(d) := \begin{cases} 1 & \begin{aligned} & \text{se $d$ è privo di quadrati ed è il prodotto} \\ & \text{di un numero pari di fattori primi} \end{aligned} \\ \\ -1 & \begin{aligned} & \text{se $d$ è privo di quadrati ed è il prodotto} \\ & \text{di un numero dispari di fattori primi} \end{aligned} \\ \\ 0 & \text{se $d$ non è privo di quadrati} \end{cases}
dove d è un intero positivo.
Nel nostro caso d è un divisore di 210, ma dato che quest’ultimo è privo di quadrati, anche d avrà la stessa proprietà, quindi \mu(d) non sarà mai zero. Inoltre, per definizione, \mu(d) = -1 se d è il prodotto di un numero dispari di fattori primi, mentre \mu(d) = 1 se d è il prodotto di un numero pari di fattori primi. Quindi possiamo riscrivere i termini positivi della formula (dove d è il prodotto di un numero pari di fattori primi) come \left\lfloor \frac{N}{d} \right\rfloor = 1 \cdot \left\lfloor \frac{N}{d} \right\rfloor = \mu(d) \left\lfloor \frac{N}{d} \right\rfloor e i termini negativi (dove d è il prodotto di un numero dispari di fattori primi) come - \left\lfloor \frac{N}{d} \right\rfloor = (-1) \cdot \left\lfloor \frac{N}{d} \right\rfloor = \mu(d) \left\lfloor \frac{N}{d} \right\rfloor, ottenendo in entrambi i casi l’espressione \mu(d) \left\lfloor \frac{N}{d} \right\rfloor.
Tenendo conto di queste due osservazioni, la formula (3) può essere riscritta come segue:
Ora la formula è molto più semplice da generalizzare, perché bisogna solo sostituire 210 con un’opportuna espressione che dipende dal nostro numero di partenza N. In questo caso, 210 è il prodotto dei primi 4 numeri primi, ossia il prodotto dei numeri primi minori o uguali di \sqrt{N} = 32, o equivalentemente, come abbiamo visto nell’articolo precedente, minori di \sqrt{N + 1}. Nell’articolo precedente abbiamo visto anche una semplice notazione per indicare il prodotto dei numeri primi minori di un certo numero z, ossia P(z). Quindi 210 = P(\sqrt{33}) = P(\sqrt{N + 1}). Quest’osservazione ci consente di scrivere la formula generale del crivello di Eratostene come segue:
Formula generale del crivello di Eratostene: espressione algebrica
Per ogni intero N \gt 1, la formula generale del crivello di Eratostene con numero di partenza N è la seguente:
dove P(\sqrt{N+1}) indica il prodotto dei numeri primi minori di \sqrt{N+1}.
Finora ci siamo concentrati sulla formula in astratto, ma abbiamo visto che questa formula è basata su un ragionamento di tipo insiemistico, il cui risultato è appunto il valore della funzione di crivello S(A, \mathbb{P}, \sqrt{N + 1}). Lo abbiamo verificato sulla base di un esempio, ma per dimostrarlo in generale dovremmo utilizzare il principio di inclusione-esclusione, la cui dimostrazione però non è rilevante per i nostri scopi, ma si ottiene tramite lo stesso meccanismo di base. Per questo motivo ometteremo la dimostrazione della seguente Proposizione:
Formula del crivello di Eratostene come funzione di crivello
Per ogni intero N \gt 1, posto A := \{1, 2, 3, \ldots, N\}, vale l’uguaglianza:
dove P(\sqrt{N+1}) indica il prodotto dei numeri primi minori di \sqrt{N+1}.
Sempre mediante il principio di inclusione-esclusione, si può dimostrare che la formula (4) vale anche se si cambia il sieving level z. Il crivello di Eratostene si ottiene con la scelta z = \sqrt{N + 1}, cioè considerando i numeri primi minori o uguali di \sqrt{N}; se cambiassimo z otterremmo un crivello diverso, che elimina da A tutti i multipli dei numeri primi minori di z, ma la formula (4) varrebbe comunque sostituendo \sqrt{N+1} con z. La generalizzazione che si ottiene è appunto l’identità di Legendre:
Identità di Legendre
Per ogni intero N \gt 1 e per ogni numero reale z \gt 1, posto A := \{1, 2, 3, \ldots, N\}, vale l’uguaglianza:
dove P(z) indica il prodotto dei numeri primi minori di z.
Come esempio vale quello che abbiamo visto all’inizio, a patto di fermarci prima dell’eliminazione dei multipli di 5. Infatti con N = 32 l’ultimo numero primo considerato dal crivello di Eratostene è 5, per cui se ci fermiamo prima (ad esempio a 3) abbiamo un crivello diverso, con un valore di z diverso (vanno bene tutti i z tali che 3 \lt z \leq 5). Nel crivello così modificato possiamo verificare la validità dell’identità di Legendre: ad esempio per 3 \lt z \leq 5 l’identità di Legendre si sviluppa nella formula 32 - \left\lfloor \frac{32}{2} \right\rfloor - \left\lfloor \frac{32}{3} \right\rfloor + \left\lfloor \frac{32}{6} \right\rfloor che, come si può vedere nella formula (c) dell’esempio, calcola correttamente il numero di elementi di A dopo aver rimosso i multipli di 2 e i multipli di 3. In sostanza, quindi, l’identità di Legendre ci dice che la formula generale del crivello di Eratostene non vale solo alla fine dell’algoritmo, ma anche nei passaggi intermedi.