Prerequirements:
In number theory, many proofs are “technical”, i.e. they consist mainly in algebrical passages, by means of which an initial expression is reduced into simpler and simpler forms, up to something which is already known. In this post we’ll see a couple of proof of this kind, that will be the occasion for learning some techniques reusable in other contexts.
We’ll prove the following lemmas:
First lemma about summations with the Möbius function and the logarithm
where the function on the left is defined for x \in \mathbb{N}^{\star}.
Second lemma about summations with the Möbius function and the logarithm
where the function on the left is defined for x \in \mathbb{N}^{\star}.
If you are following the path about the “elementary” proof of the Prime Number Theorem, in the next post you’ll see that the second Lemma will be used for proving Selberg’s Theorem, and you’ll see where it takes origin from. Apart from this, though, both Lemmas can be useful for learning some number theory techniques.
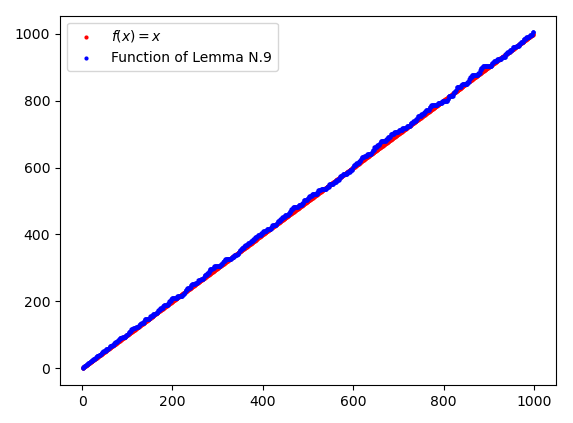
From a practical point of view, the function of Lemma N.9 seems to be approximated very well by the identity function, so much so that the two functions seem to be asymptotically equivalent:
The function of Lemma N.10 instead is approximated by the function 2x \log x in a rough way:
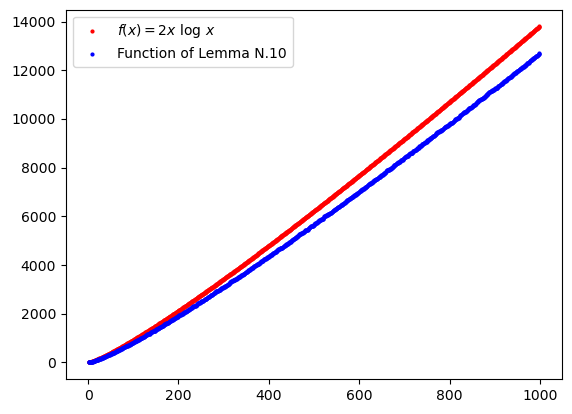
Indeed, according to Lemma N.10, when approximating the function \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left(\frac{x}{d}\right) with 2x \log x we make an error which is O(x). But empirically we can estimate this error as -x, obtaining a much better approximation:
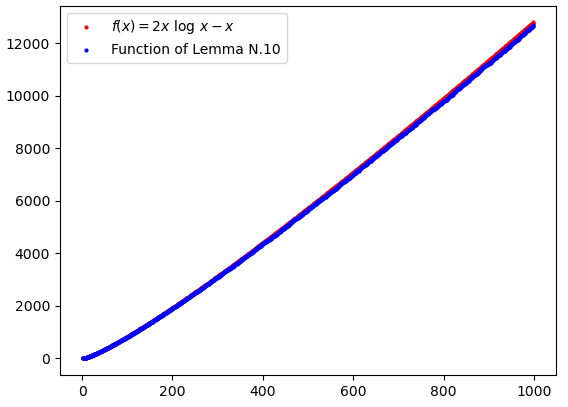
This evidence lets us think that indeed the stronger result \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left(\frac{x}{d}\right) = 2x \log x - x + o(x) may be true. If some of our readers is able to prove the truth or the falsity of this statement, he or she can contact us.
Proof of the first lemma
Let’s start to simplify the expression of the first lemma:
We can note that generally every d of the internal summation divides several n of the external summation. For example, if x = 8 then the number d = 2 divides n, with 1 \leq n \leq x, for n \in \{2, 4, 6, 8\}; so the term \mu(2) \log^2 \left(\frac{8}{2}\right) will appear four times, after both summations have been expanded. Thus, counting how many times each term appears, we can reduce the double summation to a single one. In fact, the following general Property is true:
Simplification of the double summation for n \leq x and for d \mid n
Let x be a positive integer. Let f be any function defined on positive integer numbers (the codomain does not matter(*)). Then:
(*) To be precise, it’s necessary that the sum operation is defined on the codomain, and it must be commutative. However in this context there is no problem at all, because this is true for the numerical sets we are interested in (\mathbb{N}, \mathbb{Z} and \mathbb{R}).
In order to make the proof more intuitive, we can build a table with x rows and as many columns, numbered starting from 1, where in the cell of the row r and the column c we’ll put the value f(r) if and only if r \mid c. For example, for x = 10 we’ll have the following table:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | f(1) | f(1) | f(1) | f(1) | f(1) | f(1) | f(1) | f(1) | f(1) | f(1) |
| 2 | f(2) | f(2) | f(2) | f(2) | f(2) | |||||
| 3 | f(3) | f(3) | f(3) | |||||||
| 4 | f(4) | f(4) | ||||||||
| 5 | f(5) | f(5) | ||||||||
| 6 | f(6) | |||||||||
| 7 | f(7) | |||||||||
| 8 | f(8) | |||||||||
| 9 | f(9) | |||||||||
| 10 | f(10) |
If we read this table by columns, in each column n we’ll find the value f(d) for all and only the divisors d of n. So the sum of the column n is \sum_{d \mid n} f(d), and the sum of the whole table is:
Now let’s try to read the same table by rows.
For each row n, the value of f(n) is repeated as many times as the number of multiples of n less than or equal to 10, i.e. \left \lfloor \frac{10}{n} \right \rfloor times, by Property N.5. So the sum of the row n is \left \lfloor \frac{10}{n} \right \rfloor f(n), and the sum of the whole table is:
But, since the table is the same as before, the sums (a) and (b) must be equal, hence:
We can note that the variable n represents the column number in the left summation, whereas it represents the row number in the right summation. But since we have two different summations, there is no problem in using the same symbol with a different meaning. Actually, the use of the same symbol highlights that it’s the same operation, that is the summation extended to all the positive integers less than or equal to x, regardless of what these integers represent.
Clearly the argument made so far for x = 10 can be extended to any value of x (which, remember, must be a positive integer), hence we’ll have the thesis.
It’s important to note that Property N.19 does not imply that, for all n \leq x, \sum_{d \mid n} f(d) = \left \lfloor \frac{x}{n} \right \rfloor f(n). In fact it may not be so, because as x increases the right part of the latter equality is increasing, whereas the left part remains constant. So, the equality of the summations \sum_{n \leq x} \sum_{d \mid n} f(d) and \sum_{n \leq x} \left \lfloor \frac{x}{n} \right \rfloor f(n) is true globally, not term by term.
By applying Property N.19 to formula (1), we’ll obtain:
Now let’s try to estimate the right member. As it’s often done in number theory, when there are integer parts, they can be simply removed, then estimating the error introduced this way. In our case we’ll obtain:
where we called \mathrm{Err}(x) the error, equal to - \sum_{n \leq x} \left( \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right) \mu(n) \log \left(\frac{x}{n}\right). Let’s find an overestimation of this error in absolute value:
where in the second to last passage we considered that x \leq n \Rightarrow \frac{x}{n} \geq 1 \Rightarrow \log \left(\frac{x}{n}\right) \geq 0; moreover, in the last passage, we used the fact that \left| \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right| \leq 1 and |\mu(n)| \leq 1, hence \left| \left( \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right) \mu(n)\right| = \left| \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right| |\mu(n)| \leq 1.
So we obtained the summation \sum_{n \leq x} \log \left(\frac{x}{n}\right), which we already know: in fact, by Lemma N.6 (Order of magnitude of the sum of a fraction logarithms when the denominator changes)
:
Now, joining formulas (2)-(5), we’ll have:
So the summation \sum_{n \leq x} \frac{\mu(n)}{n} \log \left(\frac{x}{n}\right) remains to be estimated. This summation is not immediately reducible to the ones we already know (like the one of Property N.12, logarithmic form (Expression of \Lambda by means of \mu), so, in order to study it, some technical artifice is needed.
The main trick is to use Theorem N.6 (Approximation of the sum of inverses of the first positive integers). By this Theorem:
Theorem N.6 is not directly applicable for computing \log \left(\frac{x}{n}\right), because \frac{x}{n} may not be an integer number. However, we can easily introduce the case of an integer number, by recalling that logarithm is an increasing function, so, since \left\lfloor \frac{x}{n}\right\rfloor \leq \frac{x}{n} \leq \left\lfloor \frac{x}{n}\right\rfloor + 1:
By applying Theorem N.6, we’ll have:
Let’s note that:
where in the central passages we applied the properties of asymptotic orders A.5 and A.8. Substituting into (a), we’ll have:
which in turn is equivalent to:
Now we can note that:
So from (b) we can obtain, by Property A.15:
hence, by Property A.13:
which is equivalent to (7).
As an alternative, we could prove an extended version of Theorem N.6, valid for real numbers. The statement and the proof would be only slightly different from the ones seen in the post The sum of the inverses of the first positive integers.
Now we can make the substitution (7) within (6), rewriting the right summation as follows:
By means of some algebraic transformations, it can be proved that the first summation is 1:
In order to simplify this summation, we can use Property N.20.
First of all we can rewrite the summation as follows:
where in the second passage we applied Property N.20 with a := n, b := k, n := x and f(a, b) := \frac{\mu(a)}{ab}.
Now let’s transform the summation further:
where in the second equality we applied Property N.14.
Now, by Property N.11, \sum_{d \mid m} \mu(d) is 1 if m = 1 and 0 otherwise, so:
Formula (9) can be obtained by joining formulas (c), (d) and (e).
The third summation instead is easily estimable as O(1):
By applying the property of asymptotic orders Corollary 1 of Property A.8, we can simplify the summation as follows:
The last summation can be overestimated in absolute value as follows:
So, by the property of asymptotic orders Property A.12, \sum_{n \leq x} \mu(n) = O(x). Finally, substituting into (f) and applying Property A.8, we’ll have:
Joining formulas (f) and (g), we’ll obtain (10).
The second summation instead, \sum_{n \leq x} \frac{\mu(n)}{n}, is difficult to estimate or to simplify, so much that we are forced to change strategy in order to eliminate it. We can note that this summation, in (8), is multiplied by \gamma: so the idea consists in eliminating \gamma, so that also the summation which multiplies it will get eliminated. This can be done by adding and subtracting \gamma to the first member of (6):
where, in the last passage, we used the fact that \sum_{d \mid n} \mu(d), by Property N.11, is 1 if n = 1 and 0 otherwise. Now, by (7), \log \left(\frac{x}{d}\right) + \gamma = \sum_{k \leq \left\lfloor \frac{x}{n} \right\rfloor} \frac{1}{k} + O\left( \frac{n}{x} \right); making this substitution, in one shot both the logarithm and the constant \gamma disappear from within the summation. Before proceeding with the substitution, though, we need logarithm in order to simplify the summation. In fact, passages (2)-(5) can be repeated with \log \left(\frac{x}{d}\right) + \gamma instead of \log \left(\frac{x}{d}\right), obtaining finally:
Proceeding as for formulas (2) and (3), putting \log \left(\frac{x}{n}\right) + \gamma in place of \log \left(\frac{x}{n}\right), we’ll obtain:
where \mathrm{Err'}(x) := - \sum_{n \leq x} \left( \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right) \mu(n) \left( \log \left(\frac{x}{n}\right) + \gamma \right ). Now,
But, coming back to the argument of formula (4), \left | \sum_{n \leq x} \left( \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right) \mu(n) \right | \leq \sum_{n \leq x} \left | \left( \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right) \mu(n) \right | \leq \sum_{n \leq x} 1 = x; so, by Property A.12, \sum_{n \leq x} \left( \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right) \mu(n) = O(x). Then, applying Corollary 2 and Corollary 3 of Property A.8, and Corollary of Property A.9:
Joining formulas (3′), (h) and (i), we’ll obtain (6′).
Now we can make the substitution given by (7) and simplify, by applying the properties of asymptotic orders Corollary of Property A.7 and Corollary of Property A.9:
Finally, putting altogether formulas (11), (6′) and (12) and applying the properties of asymptotic orders Corollary 3 of Property A.8, Corollary of Property A.7, Property A.11 and Corollary of Property A.9, we’ll have:
Thus Lemma N.9 is proved.
Proof of the second lemma
The second lemma can be proved very similarly to the first one, but calculations are a bit more complex, due to the presence of the squared logarithm. Like we did for the previous lemma, it’s convenient to eliminate the logarithm by means of (7), but in such a way that the constant \gamma remains outside of the summations. Like for (11), we have to try to obtain the term \log \left(\frac{x}{d}\right) + \gamma. In this case, because there is the squared logarithm, we can do as follows:
Now we can obtain the term \log \left(\frac{x}{d}\right) + \gamma, by decomposing the square difference \log^2 \left(\frac{x}{d}\right) - \gamma^2 as \left( \log \left(\frac{x}{d}\right) - \gamma \right)\left( \log \left(\frac{x}{d}\right) + \gamma \right). But, before doing this, let’s simplify the summation as we did in (6′):
Proceeding like for formulas (2) and (3), putting \log^2 \left(\frac{x}{n}\right) - \gamma^2 in place of \log \left(\frac{x}{n}\right), we’ll obtain:
where \mathrm{Err''}(x) := - \sum_{n \leq x} \left( \frac{x}{n} - \left \lfloor \frac{x}{n} \right \rfloor \right) \mu(n) \left( \log^2 \left(\frac{x}{n}\right) - \gamma^2 \right ). Now,
Proceeding like for formula (4), we’ll obtain:
But the right summation is O(x), by Lemma N.6A (Order of magnitude of the sum of a fraction logarithms when the denominator changes, generalized form), so by Property A.12:
Finally, (6”) follows from formulas (3”), (j) and (k).
Now, by applying (7), we can decompose the right summation as follows:
The first summation is a complicated version of (9). Making some calculations and applying some properties of the Möbius function and the function \Lambda, it can be proved that:
Proceeding like we did for (9), we can prove that:
Also in this case, like we did for formula (e), it’s convenient to distinguish between the cases m = 1 and 2 \leq m \leq x:
By the Properties N.11 and N.12 (logarithmic form), the latter expression is equal to:
In order to estimate the summation we can apply the Corollary of Proposition N.7, as follows:
So, joining formulas (m), (n) and (o) and applying Corollary of Property A.7, we’ll obtain:
hence, by (l), we’ll obtain (9′).
The second summation of (13) is very similar to (10), in fact it can be proved that the same asymptotic estimation is true:
Proceeding like we did for (10), we can prove that:
The latter summation, by applying the properties of asymptotic orders Corollary of Property A.7, Property A.5 and Corollary of Property A.9, can be estimated as follows:
where, in the second to last passage, we applied Lemma N.6 again.
So, by Property A.12, \sum_{n \leq x} \mu(n) \left( \log \left(\frac{x}{n}\right) - \gamma \right) = O(x): by putting this into (p) we’ll obtain (10′).
The proof terminates by putting altogether the previous formulas and by applying the same properties of asymptotic orders already applied before: