Our research about Goldbach’s Conjecture led us, at one point, to extend the definition of linear dashed line. As we know, a linear dashed line is a function represented by a table with k rows and infinite numbered columns starting from 1, where, in each row, a dash appears for each column whose number is a multiple of a given fixed positive integer (one of the components of the dashed line). Sometimes it is necessary to consider tables in which the dashes appear not only in correspondence with the multiples, but also in correspondence with the numbers that have a certain fixed remainder, modulo one or more components.
For example, let’s start with the dashed line (2, 3, 5, 7) represented up to 25:
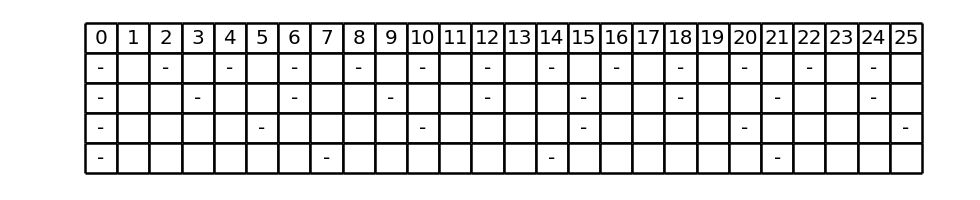
By definition, dashes appear on the first row for multiples of 2, on the second row for multiples of 3, on the third row for multiples of 5, on the fourth row for multiples of 7.
Now let’s try to modify the dashed line as follows:
- We leave the first and third rows as they are;
- On the second row, whose component is 3, we add dashes in correspondence with the numbers that have remainder 1 modulo 3;
- On the fourth row, whose component is 7, we add dashes in correspondence with the numbers that have remainder 2 modulo 7.
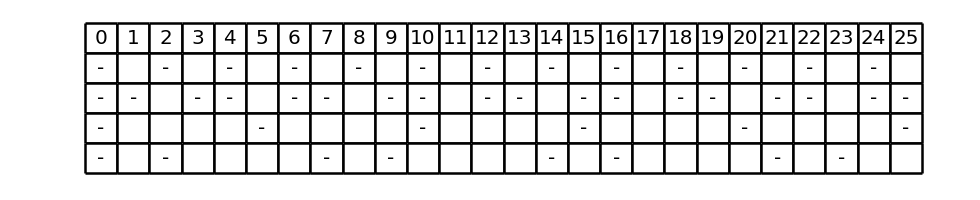
What we got is an example of what we will name “double dashed line”. In a double dashed line, therefore, there can exist rows identical to the ones of the linear dashed lines, with dashes only in correspondence with the multiples, and rows where the dashes appear both in correspondence with the multiples of the relative component (i.e. the numbers that have remainder 0 modulo the component), and in correspondence of the numbers that have a given remainder, different from zero, modulo the component. If, as in the previous Figures, we start from a linear dashed line T to obtain a double dashed line that keeps the dashes of T and adds others, then the double dashed line is said “based on T“.
To reinforce the contrast with double dashed lines, linear dashed lines are sometimes also called single dashed lines. Both double and single dashed lines fall under the general definition of dashed line, which is deliberately very generic, so that it is possible to construct different classes of dashed lines according to one’s needs. Just as in the single dashed lines the components can be chosen arbitrarily, in double dashed lines the remainders can be chosen as desired, for example they may not all be different.
If we wanted to write the mathematical function corresponding to the dashed line in Figure 2, which we can name U, we would get something like the following:
In general, starting from a generic linear dashed line T, the following definition of double dashed line is obtained, which incorporates and extends the Definitions T.1 (Dashed line) and T.2 (Linear dashed line):
Linear double dashed line
Let T = (n_1, \ldots, n_k) be a linear dashed line of order k with set of indices I. Let r_1, \ldots, r_k be integers such that, for each i = 1, \ldots, k, we have 0 \leq r_i \lt n_i. We then define the dashed line T^{(r_1, \ldots, r_k)}: I \times \mathbb{N} \Rightarrow \mathbb{N} such that:
It is said to be a linear double dashed line (or simply double dashed line) based on T, with displacements r_1 , \ldots, r_k.
The technicalities of the definition aren’t important; instead, it is important to remember that the numbers r_1, \ldots, r_k are called displacements and are the additional remainders on the basis of which, on each line, further dashes are inserted with respect to the starting linear dashed line. In particular, the lines in which no additional dashes have been inserted are considered as having displacement 0: for example, if we indicate the dashed line of Figure 1 with T, then the dashed line of Figure 2 is called “double dashed line based on T with displacements 0, 1, 0, 2” and denoted by T^{(0, 1, 0, 2)}. We observe that, when r_i = 0, the row i of the double dashed line coincides with the one of the starting linear dashed line, i.e. it has no additional dashes, as seen in this example for i = 1 and i = 3.
As we mentioned at the beginning, double dashed lines are important for the study of Goldbach’s Conjecture. To learn more about this, we refer readers to the proof strategy based on spaces.